Применение ИКТ на уроках математики Из опыта работы Ивановой Т. А.

«Знание, добытое без личного усилия, без личного напряжения, – знание мертвое. Только пропущенное через собственную голову становится твоим достоянием». Нойгуузер

«Наука без практики
похожа на стоячую воду,
а ум человека,
не находя себе применения, чахнет»
«трактат о живописи»
Леонардо да Винчи

Специалист должен
Самостоятельно критически мыслить
Грамотно работать с информацией
Самостоятельно работать над развитием собственной нравственности, интеллекта, культурного уровня
Быть коммуникабельными, контактными в различных социальных группах
Гибко адаптироваться в меняющихся жизненных ситуациях

Процесс организации обучения с использованием ИТ позволяет
Сделать этот процесс интересным
Эффективно решать проблему наглядности
Индивидуализировать процесс обучения
Раскрепостить студентов при ответе
Осуществлять самостоятельную учебно-исследовательскую деятельность

ИКТ используются в формах
Самостоятельное изучение с помощью УМК
Тренировочных программ
Использования контролирующих средств
Домашних самостоятельных и творческих заданий

Этапы обучения
Объяснение нового материала
Закрепление
Контроль

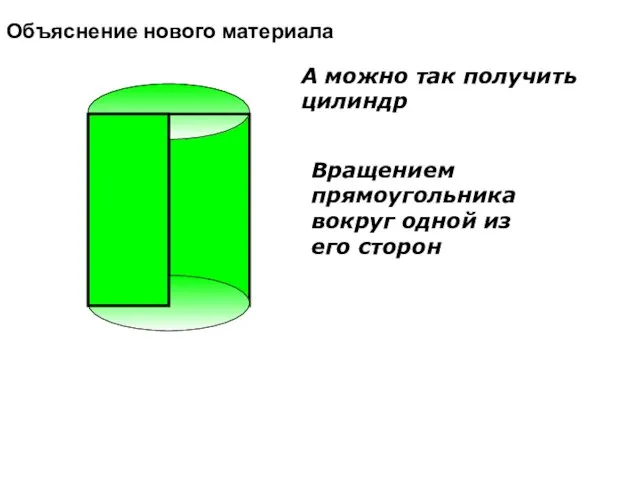
А можно так получить цилиндр
Вращением прямоугольника вокруг одной из его сторон
Объяснение нового материала

ЗНАНИЕ ТЕОРИИ ОБЯЗАТЕЛЬНО!!!
Механический смысл производной

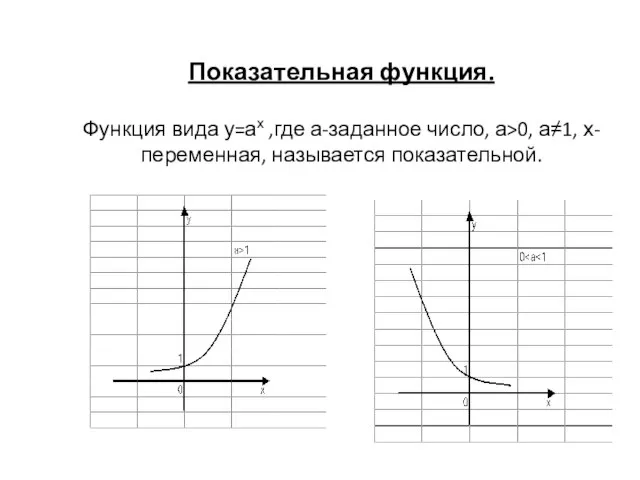
Показательная функция.
Функция вида у=ах ,где а-заданное число, а>0, а≠1, х-переменная, называется показательной.

Показательные уравнения.
Уравнения,у которых неизвестное находится в показателе степени, называются показательными.
Способы решения:
По свойству степени;
Вынесение общего множителя за скобки;
Деление обеих частей уравнения на одно и то же выражение,принимающее значение отличное от нуля при всех действительных значениях х;
Способ группировки;
Сведение уравнения к квадратному;
Графический.
.
Например:

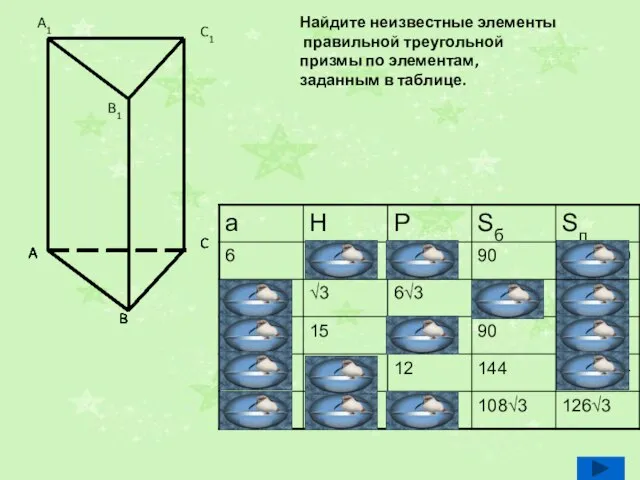
Найдите неизвестные элементы
правильной треугольной
призмы по элементам,
заданным в таблице.
A
B
C
A
A
B
C
A
B
C
A
B
C
A
B
C
A
B
C
A
B
A

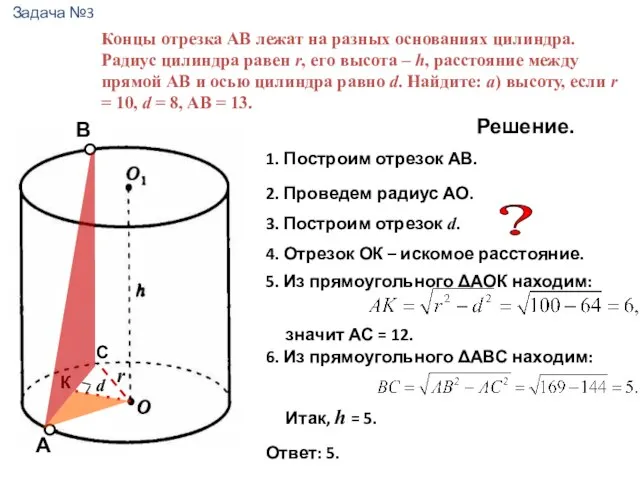
Концы отрезка АВ лежат на разных основаниях цилиндра. Радиус цилиндра равен r, его высота – h, расстояние между прямой АВ и осью цилиндра равно d. Найдите: a) высоту, если r = 10, d = 8, AB = 13.
r
a
Решение.
1. Построим отрезок АВ.
2. Проведем радиус АО.
3. Построим отрезок d.
?
r
d
К
4. Отрезок ОК – искомое расстояние.
5. Из прямоугольного ΔАОК находим:
С
значит АС = 12.
6. Из прямоугольного ΔАВС находим:
Итак, h = 5.
Ответ: 5.
Задача №3

Домашняя работа

Кому принадлежат слова:
«Математику уже затем изучать нужно, что она ум в порядок приводит»?
Первая тройка игроков

Л
в
м
о
н
о
с
о
о
в
с

Задание №1. «Испытание до первого успеха»
Условие:
Сколько в среднем раз надо бросать кость до появления шестерки?

Ответ: Кажется ясным, что ответ должен быть 6. Чтобы это проверить, обозначим через p вероятность появления шестерки. Тогда вероятности первого успеха при данном испытании равны (q=1-p)
Сумма вероятностей равна p+pq+pq2+...=p(1+q+q2+...)=p/(1-q)=p/p=1. Среднее число испытаний m до первого успеха по определению равно m=p+2pq+3pq2+4pq3+...
Для нахождения суммы такого ряда применим обычный прием суммирования геометрических рядов qm=pq+2pq2+3pq3+...

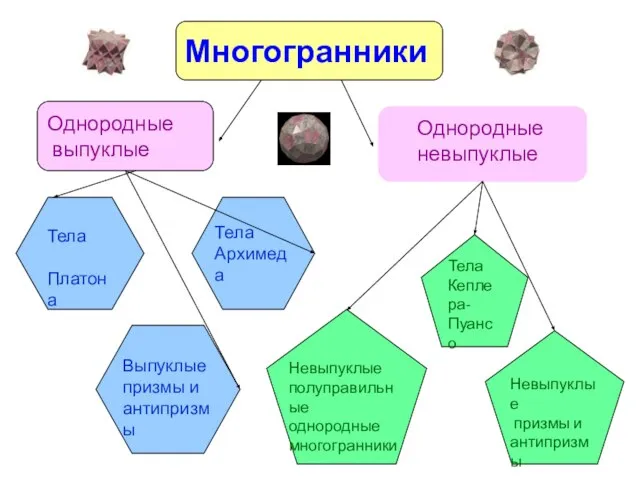
Многогранники
Однородные
выпуклые
Однородные невыпуклые
Тела
Архимеда
Тела
Платона
Выпуклые
призмы и
антипризмы
Тела
Кеплера-
Пуансо
Невыпуклые
полуправильные
однородные
многогранники
Невыпуклые
призмы и
антипризмы

Правильные многогранники
Сколько же их существует?
Рассмотрим развертку вершины многогранника. Каждая вершина может принадлежать трем и более граням.
Сначала рассмотрим случай, когда грани многогранника - равносторонние треугольники. Поскольку внутренний угол равностороннего треугольника равен 60°, три таких угла дадут в развертке 180°. Если теперь склеить развертку в многогранный угол, получится тетраэдр - многогранник, в каждой вершине которого встречаются три правильные треугольные грани. Если добавить к развертке вершины еще один треугольник, в сумме получится 240°. Это развертка вершины октаэдра. Добавление пятого треугольника даст угол 300° - мы получаем развертку вершины икосаэдра. Если же добавить еще один, шестой треугольник, сумма углов станет равной 360° - эта развертка, очевидно, не может соответствовать ни одному выпуклому многограннику.

Теперь перейдем к квадратным граням. Развертка из трех квадратных граней имеет угол 3x90°=270° - получается вершина куба, который также называют гексаэдром. Добавление еще одного квадрата увеличит угол до 360° - этой развертке уже не соответствует никакой выпуклый многогранник.
Три пятиугольные грани дают угол развертки 3*108°=324 - вершина додекаэдра. Если добавить еще один пятиугольник, получим больше 360° - поэтому останавливаемся.
Для шестиугольников уже три грани дают угол развертки 3*120°=360°, поэтому правильного выпуклого многогранника с шестиугольными гранями не существует. Если же грань имеет еще больше углов, то развертка будет иметь еще больший угол. Значит, правильных выпуклых многогранников с гранями, имеющими шесть и более углов, не существует.

Сделаем вывод:
Мы убедились, что существует лишь пять выпуклых правильных многогранников - тетраэдр, октаэдр и икосаэдр с треугольными гранями, куб (гексаэдр) с квадратными гранями и додекаэдр с пятиугольными гранями.
Эти тела еще называют
телами Платона.

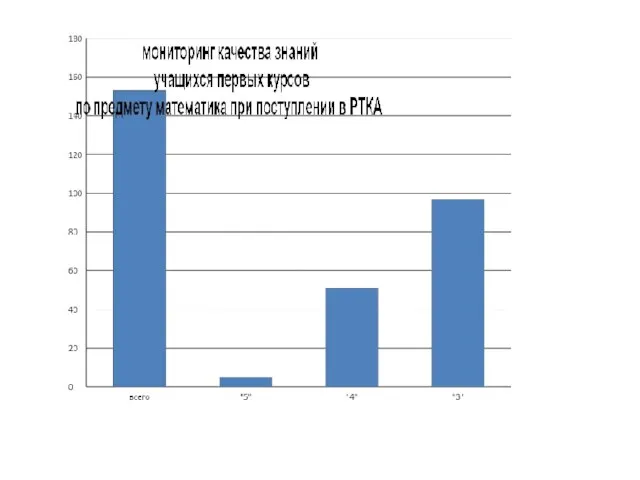
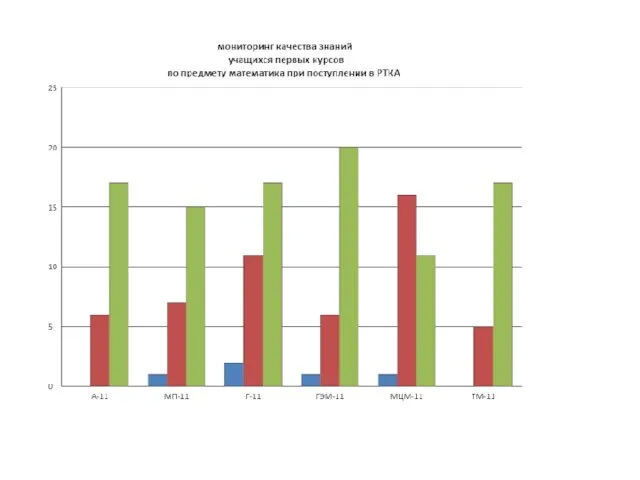
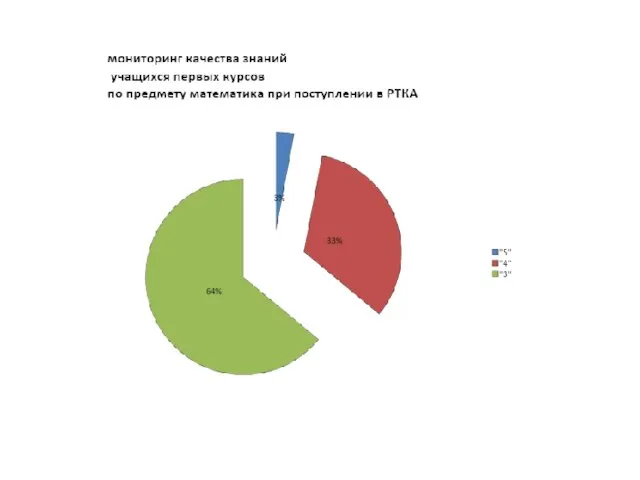
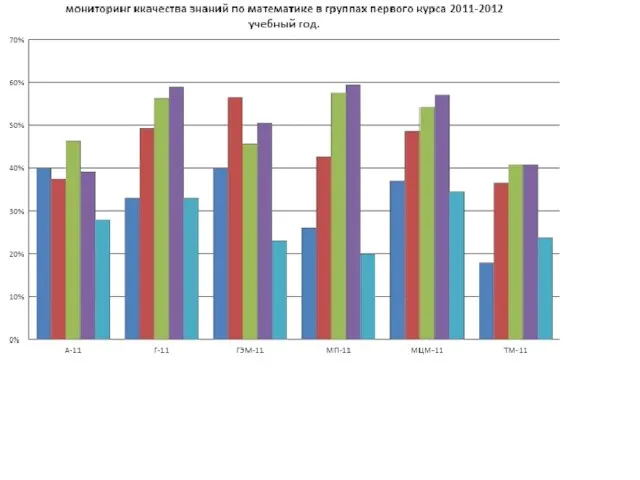
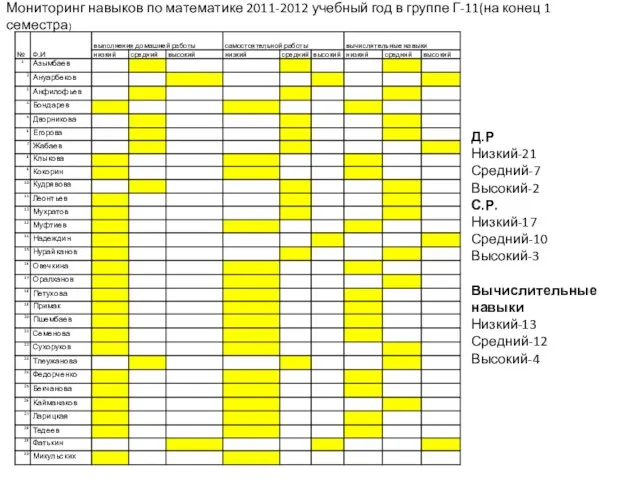
Мониторинг навыков по математике 2011-2012 учебный год в группе Г-11(на конец 1 семестра)
Д.Р
Низкий-21
Средний-7
Высокий-2
С.Р.
Низкий-17
Средний-10
Высокий-3
Вычислительные навыки
Низкий-13
Средний-12
Высокий-4