Содержание
- 2. Прогноз по данным временного ряда, содержащим сезонную компоненту При составлении прогноза сезонную компоненту можно учесть как
- 3. 1) Первый этап заключается в определении структуры сезонных изменений и периода этих колебаний. Например, через каждые
- 4. Если m-четное, то задача несколько усложняется, так как средние точки будут расположены между точками, по которым
- 5. Для мультипликативной модели (7.5) при первом варианте оценки тренда находится отношение фактических значений показателя к расчетным,
- 6. 4) Четвертый этап- прогнозирование на основе данных, из которых исключена сезонная составляющая. Этот этап выполняется в
- 7. Пример 1. В таблице представлены поквартальные данные о количестве реализованных единиц товара за три года. По
- 8. Результаты расчета представлены в пятом столбце:
- 9. Оценим сезонную составляющую аддитивной модели (см. формулу 7.4) как разность между фактическим размером реализации и значением
- 10. В моделях с сезонной компонентой предполагается, что сезонные воздействия за период взаимопогашаются (т.е. сумма значений сезонных
- 12. Рассмотрим мультипликативную модель прогноза. Рассчитаем средние индексы сезонности. Для первого квартала индекс сезонности равен: Для второго:
- 13. Ошибка модели прогноза рассчитывается по формуле: ( )
- 14. Экспоненциальное сглаживание с тремя параметрами, отражающими тренд и сезонность изменений. Данная модель была предложена Винтерсом. Считается,
- 15. Где - сглаженное значение ряда; - параметр сглаживания данных; - фактическое значение показателя для периода t;
- 16. Следует отметить, что начальных условий для сезонности столько, каков период сезонных колебаний, т. е., например, если
- 17. Анализ Фурье. При применении этого метода сначала также оценивается и удаляется тренд. Для полученных остатков подбирается
- 18. Экспертные методы прогнозирования Процедура получения экспертных оценок может быть формализована и представлена в виде блок-схемы.
- 20. Формирование группы экспертов- Остановимся на количественной стороне выбора экспертов. Известно, что при прогнозировании в целях минимизации
- 21. Комбинированная оценка прогноза Для получения комбинированной оценки прогноза необходимо решить две задачи: 1. Установить область, внутри
- 23. Сначала формируется база исходных данных для комбинированного прогноза, которыми являются прогнозные значения, полученные разными методами. Исходные
- 25. Скачать презентацию
Слайд 2Прогноз по данным временного ряда, содержащим сезонную компоненту
При составлении прогноза сезонную компоненту
Прогноз по данным временного ряда, содержащим сезонную компоненту
При составлении прогноза сезонную компоненту

аддитивную составляющую или в виде индекса сезонности. В теории
прогнозирования разработаны несколько способов учета сезонности,
рассмотрим некоторые из них.
Учет сезонности в трендовых моделях прогнозирования.
Алгоритм прогнозирования с учетом сезонной составляющей по
трендовым моделям (формулы (7.4) и (7.5)) состоит из пяти этапов.
Слайд 31) Первый этап заключается в определении структуры сезонных
изменений и периода этих колебаний.
1) Первый этап заключается в определении структуры сезонных
изменений и периода этих колебаний.

4 квартала “поведение” показателя повторяется; если данные
собраны по месяцам, то структура сезонных колебаний будет
повторяться каждые 12 месяцев. Если значение показателя существенно
изменяется по дням недели, то можно говорить о “сезонных” колебаниях
периодичностью 7дн.
2) Второй этап- это оценка и исключение тренда. Для оценки тренда могут
использоваться два варианта: линии (кривые) тренда или метод
скользящих средних. Уделим внимание второму варианту оценки тренда.
Метод скользящих средних предусматривает вычисление
последовательности скользящих средних по m узлам, где
m- продолжительность сезонных колебаний.
Если m-нечетное, то первое значение скользящего среднего (среднее от
первого до m-гo значения ряда) присваивается (m + 1 )/2 точке.
Аналогично следующее значение скользящего среднего (среднее от
второго до (m + 1)-гo значения назначается (m + 3)/2 точке и т. д.).
Слайд 4Если m-четное, то задача несколько усложняется, так как средние
точки будут расположены
Если m-четное, то задача несколько усложняется, так как средние
точки будут расположены

расчет. Например, если m = 4, то первое скользящее среднее
окажется между второй и третьей точками, второе скользящее
среднее между третьей и четвертой и т. д. В этом случае требуется
процедура центрирования полученных значений.
Центрированное значение находится как среднее от двух скользящих
средних, находящихся между точками. Например, центрированное
значение для третьей точки это среднее от скользящих средних,
расположенных между второй и третьей, третьей и четвертой точками.
Необходимо отметить, что полученные значения скользящих средних уже
не содержат сезонной компоненты, поскольку представляют среднюю
величину за определенный период.
3) Третий этап- определение сезонной компоненты. Расчеты зависят от
выбора вида модели прогноза.
Для аддитивной модели (7.4) рассчитывается оценка сезонной компоненты
как разность между фактическим значением и значением, определенным
по трендовой модели (первый вариант оценки тренда). Или фактическим
значением и скользящей средней (при нечетном m), или фактическим
значением и центрированной средней (при четном m), если использовался
второй вариант оценки тренда.
Слайд 5Для мультипликативной модели (7.5) при первом варианте оценки
тренда находится отношение фактических
Для мультипликативной модели (7.5) при первом варианте оценки
тренда находится отношение фактических

расчетным, определенным по трендовой модели. Во втором варианте
оценки тренда находится отношение фактических значений показателя
к скользящей средней (при нечетном m) или к центрированной средней
(при четном m). Такое отношение называется индексом (коэффициентом)
сезонности.
Для того чтобы дальше использовать значения сезонной компоненты и
коэффициентов сезонности, необходимо найти средние значения оценок
(коэффициентов) для каждого сезона. Далее полученные средние значения
следует скорректировать таким образом, чтобы сумма оценок сезонной
компоненты для аддитивной модели равнялась нулю (это позволит
усреднить значения сезонной компоненты за весь период колебаний), а
сумма коэффициентов (индексов) сезонности равнялась числу сезонов.
Если в аддитивной модели из фактического значения вычесть сезонную
компоненту, а в мультипликативной модели фактическое значение
разделить на индекс сезонности, то получим данные, в которых нет
сезонности.
Слайд 64) Четвертый этап- прогнозирование на основе данных, из которых
исключена сезонная составляющая. Этот
4) Четвертый этап- прогнозирование на основе данных, из которых
исключена сезонная составляющая. Этот

случае, если на втором этапе мы выбрали для оценки тренда метод
скользящих средних. Для прогнозирования выбирается трендовая
модель с помощью метода наименьших квадратов или экспоненциальное
сглаживание. После исключения из исходных данных сезонности и тренда
остается случайная составляющая, отражающая присутствие не
поддающихся учету и прогнозу факторов.
5) Пятый этап- вычисление ошибки модели прогноза. Из фактического
значения вычитаются сезонная компонента и тренд (аддитивная модель),
для полученных остатков определяется среднее квадратическое
отклонение. В мультипликативной модели из фактического значения
вычитается произведение индекса сезонности и тренда. По полученным
остаткам также рассчитывается ошибка прогноза. Следует напомнить, что
чем больше период упреждения прогноза, тем его точность будет меньше.
Слайд 7Пример 1. В таблице представлены поквартальные данные о количестве
реализованных единиц товара за
Пример 1. В таблице представлены поквартальные данные о количестве
реализованных единиц товара за
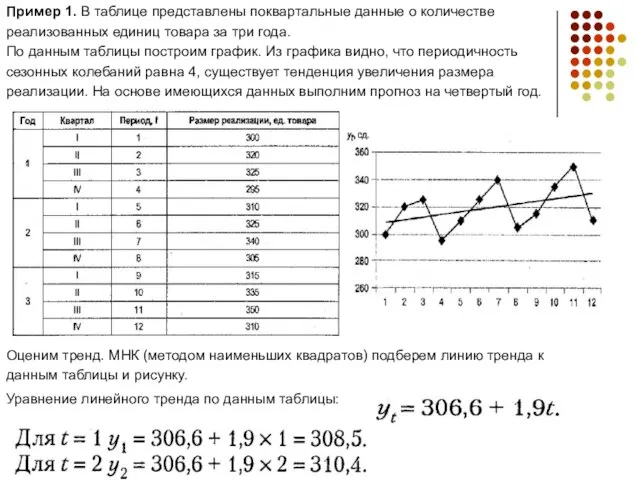
По данным таблицы построим график. Из графика видно, что периодичность
сезонных колебаний равна 4, существует тенденция увеличения размера
реализации. На основе имеющихся данных выполним прогноз на четвертый год.
Оценим тренд. МНК (методом наименьших квадратов) подберем линию тренда к
данным таблицы и рисунку.
Уравнение линейного тренда по данным таблицы:
Слайд 8Результаты расчета представлены в пятом столбце:
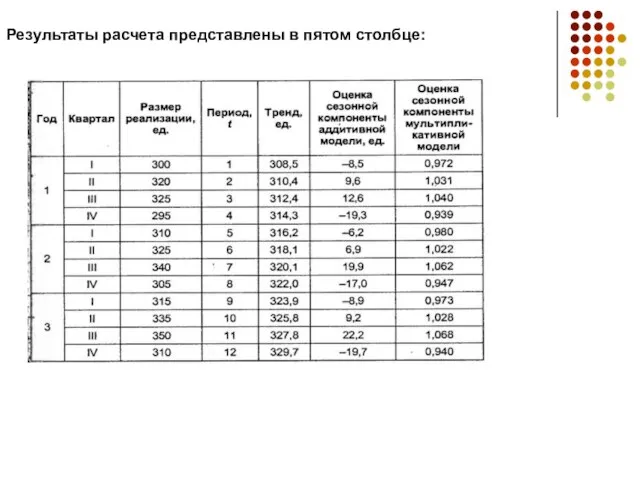
Слайд 9Оценим сезонную составляющую аддитивной модели (см. формулу 7.4)
как разность между фактическим
Оценим сезонную составляющую аддитивной модели (см. формулу 7.4)
как разность между фактическим

Для t=1 оценка сезонной компоненты равна
Для t=2 Оценки сезонной компоненты аддитивной
модели представлены в шестом столбце.
Оценим сезонную составляющую мультипликативной модели (см. формулу 7.5) как
отношение фактического размера реализации к значению тренда. Для t=1 оценка сезонной
компоненты равна Для t=2
Результаты определения сезонной составляющей для мультипликативной модели
представлены в последнем столбце.
Полученные оценки сезонной компоненты пока еще не пригодны для построения прогнозов,
поскольку они показывают сезонное отклонение от тренда для конкретного периода времени
в исходном ряду. Для того чтобы оценки сезонности можно было использовать в целях
получения более точного прогноза, скорректированного с учетом сезонных изменений,
необходимо найти средние оценки сезонной компоненты.
Рассмотрим аддитивную модель. Средняя оценка сезонной компоненты для первого
квартала равна:
Для второго квартала:
Для третьего и четвертого
Слайд 10В моделях с сезонной компонентой предполагается, что сезонные воздействия
за период взаимопогашаются
В моделях с сезонной компонентой предполагается, что сезонные воздействия
за период взаимопогашаются

равна нулю. Определим сумму: -7,9+8,6+18,2-18,7=0,2
Определим корректирующий коэффициент: k=0,2/4=0,05
Скорректированные значения сезонной компоненты рассчитываются как разность
между ее средней оценкой и корректирующим коэффициентом k. Для первого
квартала: -7,9-0,05=-7,95ед. для второго 8,55 и т.д. …
Проверим условие равенства нулю суммы скорректированных значений:
-7,95+8,55+18,15-18,75=0 Таким образом полученные значения сезонной компоненты
рассчитаны верно, и они могут использоваться в аддитивной модели прогноза.
Найдем прогноз на один год по трендовой модели и скорректируем его с учетом сезонности.
Продолжим тренд на 13-й, 14-й, 15 и 16-й кварталы и рассчитаем значение размера
реализации на основе выявленной тенденции, для этого в уравнение
вместо t подставим значения 13-й, 14, 15 и 16-й. Затем к полученным значениям прибавим
оценку сезонной компоненты.
Для первого квартала (t=13) прогнозное значение равно
Для второго квартала
и т.д.
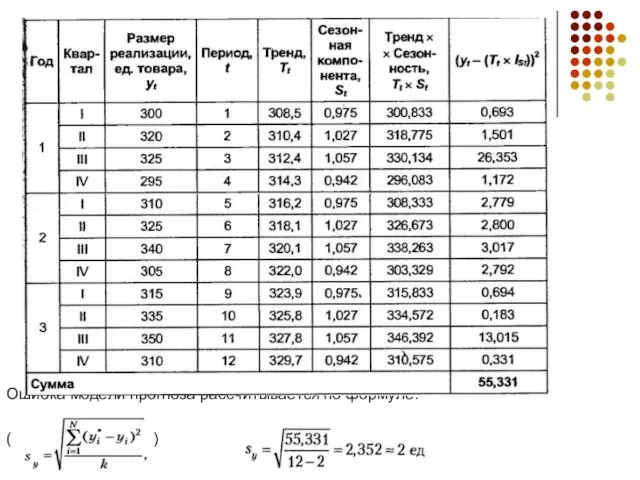
Расчет ошибки, которую дает рассмотренная модель прогноза, показан в следующей
таблице. Ошибка модели прогноза рассчитывается по формуле
( )
Слайд 12Рассмотрим мультипликативную модель прогноза. Рассчитаем средние индексы
сезонности. Для первого квартала индекс
Рассмотрим мультипликативную модель прогноза. Рассчитаем средние индексы
сезонности. Для первого квартала индекс

Для второго:
и т.д.
Взаимопогашаемость сезонных воздействий в мультипликативной модели
выражается в том, что сумма значений сезонной компоненты по отдельным
периодам должна быть равна числу периодов в цикле. В нашем примере число периодов в
цикле равно четырем. Найдем сумму средних оценок сезонной компоненты:
0,975+1,027+1,057+0,942=4,002
Определим корректирующий коэффициент: k=4/4.002=0,9998=>1
Скорректированные значения сезонной компоненты или индексы сезонности равны
произведению средних оценок и корректирующего коэффициента. В нашем примере
индексы сезонности не претерпят существенных изменений, поскольку корректирующий
коэффициент практически равен 1. Полученные значения индексов сезонности могут
использоваться в моделях прогнозов.
Найдем прогноз на четвертый год с помощью мультипликативной модели. Для первого
квартала (t = 13) прогноз размера реализации равен
и т.д.
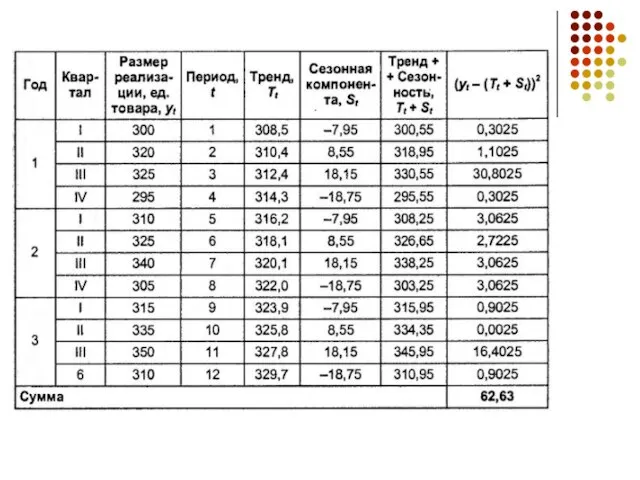
Расчет ошибки, которую дает рассмотренная модель прогноза, показан в след. таблице:
Слайд 13
Ошибка модели прогноза рассчитывается по формуле:
( )
Ошибка модели прогноза рассчитывается по формуле:
( )
Слайд 14Экспоненциальное сглаживание с тремя параметрами,
отражающими тренд и сезонность изменений. Данная модель была
предложена
Экспоненциальное сглаживание с тремя параметрами,
отражающими тренд и сезонность изменений. Данная модель была
предложена

повысить точность прогноза, когда временной ряд включает тренд и
сезонные колебания. Модель Винтерса включает четыре уравнения:
сглаживание исходного ряда:
сглаживание тренда:
оценка сезонности:
прогноз на p периодов вперед:
Слайд 15Где - сглаженное значение ряда;
- параметр сглаживания данных;
- фактическое
Где - сглаженное значение ряда;
- параметр сглаживания данных;
- фактическое

- параметр сглаживания для оценки тренда;
- оценка тренда;
- параметр сглаживания для оценки сезонности;
- оценка сезонности;
p - количество периодов, на которое строится прогноз;
s - длительность периода сезонных колебаний.
Параметры сглаживания должны соответствовать условиям:
Прежде чем применять уравнения, необходимо задать начальные условия.
Существует два варианта выбора начальных условий в модели Винтерса.
Первый предполагает, что начальное значение сглаженного ряда (Ls)
равно первому наблюдению. Тогда тренд (Тs) равен нулю, а
коэффициенты сезонности (St-s) устанавливаются равными 1.
Слайд 16Следует отметить, что начальных условий для сезонности
столько, каков период сезонных колебаний,
Следует отметить, что начальных условий для сезонности
столько, каков период сезонных колебаний,

Период колебаний равен 4 (поквартальная сезонность), то требуется
установить 4 начальных условия для сезонности.
Второй вариант назначения начальных условий предполагает, что
начальное значение для сглаженного ряда (Lt-1) равно среднему
значению за первые s наблюдений. Тогда начальные условия для тренда
(Tt-1) определяются наклоном прямой, образованной этими наблюдениями.
Коэффициенты сезонности равны
где Ls- начальное условие для сглаживания данных.
Слайд 17Анализ Фурье.
При применении этого метода сначала также оценивается и удаляется
тренд.
При применении этого метода сначала также оценивается и удаляется
тренд.

описывается формулой:
Где параметры модели, k- номер гармоники (обычно от 1 до 4).
Параметры модели определяются по МНК. Для применения этого метода
необходимо, чтобы количество точек исходного ряда являлось степенью
числа 2, например 2, 4, 8, 16…
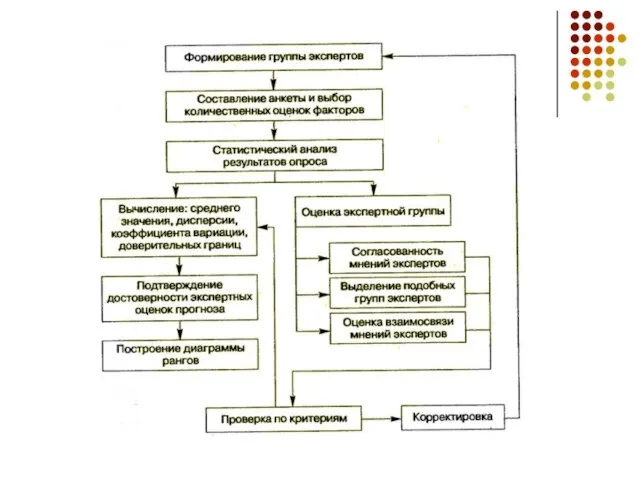
Слайд 18Экспертные методы прогнозирования
Процедура получения экспертных оценок может быть формализована и
представлена в виде
Экспертные методы прогнозирования
Процедура получения экспертных оценок может быть формализована и
представлена в виде

Слайд 20Формирование группы экспертов- Остановимся на количественной
стороне выбора экспертов. Известно, что при прогнозировании
Формирование группы экспертов- Остановимся на количественной
стороне выбора экспертов. Известно, что при прогнозировании

минимизации расходов на прогноз стремятся привлекать минимальное
число экспертов при условии обеспечения ошибки результата
прогнозирования не более Е, где 0 < Е < 1. Поэтому рекомендуемое число
экспертов может быть определено по формуле
При подстановке предельных значений Е в формулу получим, что
минимальное количество экспертов равно 4.
Для определения максимальной численности экспертной группы
используется неравенство:
где Кi- компетентность i-гo эксперта, рассчитанная на основе анкеты
самооценки или иным способом; Kmax- максимально возможная
компетентность по используемой шкале компетентности экспертов.
После определения числа экспертов переходят к поиску специалистов,
отбор которых начинается с составления списка компетентных в данной
области лиц. Далее все процедуры выбора экспертов основываются на
составленном списке.
Слайд 21Комбинированная оценка прогноза
Для получения комбинированной оценки прогноза необходимо решить две
задачи:
1.
Комбинированная оценка прогноза
Для получения комбинированной оценки прогноза необходимо решить две
задачи:
1.

разными методами, могут считаться согласованными.
2. Установить такое соотношение между результатами прогнозов, которое
наиболее адекватно отражало бы их связь с наиболее вероятным
результатом прогнозирования.
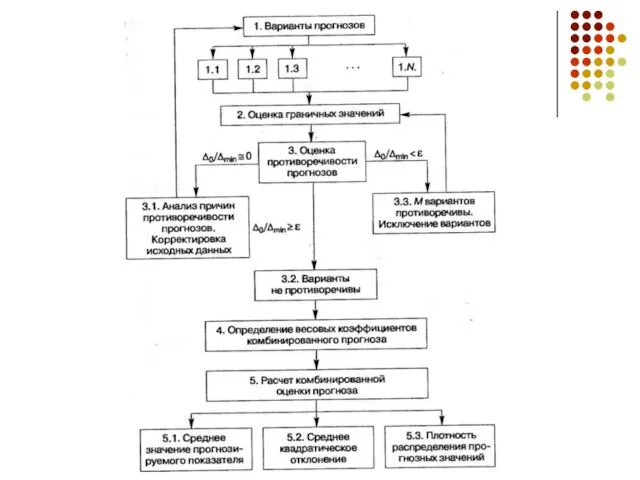
Далее представлена общая схема получения комбинированного прогноза.
Слайд 23Сначала формируется база исходных данных для комбинированного прогноза,
которыми являются прогнозные значения, полученные
Сначала формируется база исходных данных для комбинированного прогноза,
которыми являются прогнозные значения, полученные

Исходные данные должны быть представлены в аналогичном виде. Если
математический прогноз представлен в виде функции распределения, значит,
необходимо получить вероятностную оценку значений прогнозируемой величины,
полученных эвристическим методом.
Затем оцениваются резко выделяющиеся значения средних оценок прогнозируемого
показателя, полученных разными методами. На этом этапе некоторые варианты прогнозов
могут быть исключены из комбинированной оценки. Следующим шагом является оценка
противоречивости прогнозов. Для решения этой задачи существует несколько методов, мы
рассмотрим два из них. Первый метод предусматривает сравнение точечных и
интервальных прогнозов. Точечные прогнозы, естественно, могут не совпадать. При
сравнении интервальных прогнозов возможны три случая
1) Доверительные интервалы не имеют общей области:
В этом случае проводится логический анализ причин противоречивости прогнозов,
корректируются исходные данные, и проводится повторная проверка согласованности
откорректированных прогнозов.
2) Доверительный интервал одного прогноза полностью охватывает доверительный
интервал другого прогноза. При этом общая часть равна меньшему доверительному
интервалу.
3) Доверительные интервалы частично перекрываются.
 Презентация на тему Алгебра и логика высказываний
Презентация на тему Алгебра и логика высказываний Заболевание височно-нижнечелюстного сустава
Заболевание височно-нижнечелюстного сустава  Конфликтный треугольник: семья-ребенок-образовательное учреждение. Детская агрессия
Конфликтный треугольник: семья-ребенок-образовательное учреждение. Детская агрессия кольцово
кольцово Проблемы преемственности начального и основного (общего) образования
Проблемы преемственности начального и основного (общего) образования Проектная деятельность
Проектная деятельность Власть. Структурная и ситуационная власть
Власть. Структурная и ситуационная власть Свечникова В.В. правоведение тема 2 презентация
Свечникова В.В. правоведение тема 2 презентация Майолика. Гутные изделия. Ковка
Майолика. Гутные изделия. Ковка Saint Petersburg state University
Saint Petersburg state University 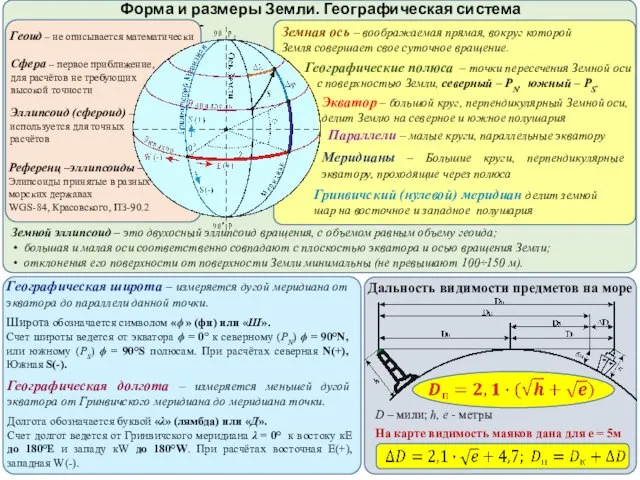 Форма и размеры Земли
Форма и размеры Земли Поздравление крестной жениха
Поздравление крестной жениха Гендерные аспекты образования и рынка труда
Гендерные аспекты образования и рынка труда Геометрия на службе у архитектуры
Геометрия на службе у архитектуры Психология двигательно-волевой сферы психической деятельности
Психология двигательно-волевой сферы психической деятельности Команда звёздочки
Команда звёздочки История семейного образования в СанктПетербурге
История семейного образования в СанктПетербурге Русский пейзаж в поэзии и живописи
Русский пейзаж в поэзии и живописи Физическая культура в период самоизоляции студентов педагогического вуза
Физическая культура в период самоизоляции студентов педагогического вуза Заповедники России
Заповедники России Презентация на тему Прощание с 1 классом
Презентация на тему Прощание с 1 классом Клёш и фалды
Клёш и фалды Быть нормальным
Быть нормальным Основные формы рельефа Алтайского края
Основные формы рельефа Алтайского края  Проект: Комплексное сопровождение покупки страховой компании
Проект: Комплексное сопровождение покупки страховой компании Сделка. Предпринимательская деятельность
Сделка. Предпринимательская деятельность русский язык - язык международного общения
русский язык - язык международного общения Условия признания и исполнения иностранных судебных решений
Условия признания и исполнения иностранных судебных решений