Применение теоремы Пифагора

Применение теоремы Пифагора
в геометрии
Рассмотрим примеры практического применения теоремы Пифагора. Не будем пытаться привести все примеры использования теоремы - это вряд ли было бы возможно. Область применения теоремы достаточно обширна и вообще не может быть указана с достаточной полнотой. Определим возможности, которые дает теорема Пифагора для вычисления длин отрезков некоторых фигур на плоскости. Диагональ d квадрата со стороной а можно рассматривать как гипотенузу прямоугольного равнобедренного треугольника с катетом а. Таким образом,
d=2a,
откуда:
d=2a².

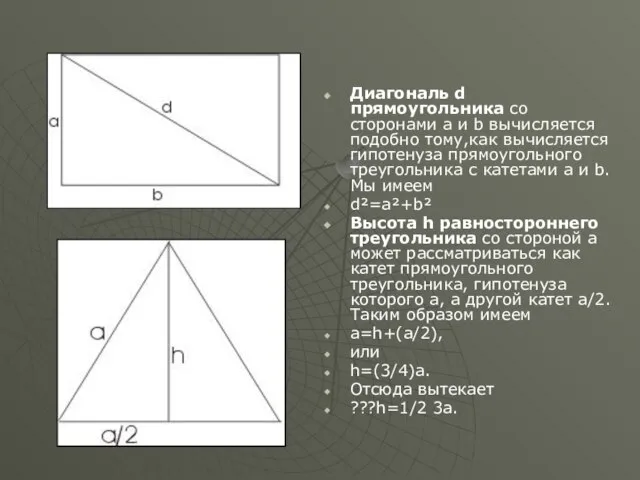
Диагональ d прямоугольника со сторонами а и b вычисляется подобно тому,как вычисляется гипотенуза прямоугольного треугольника с катетами a и b. Мы имеем
d²=a²+b²
Высота h равностороннего треугольника со стороной а может рассматриваться как катет прямоугольного треугольника, гипотенуза которого а, а другой катет a/2. Таким образом имеем
a=h+(a/2),
или
h=(3/4)a.
Отсюда вытекает
???h=1/2 3a.

Не только планиметрия
Возможности применения теоремы Пифагора к вычислениям не ограничиваются планиметрией. На рисунке изображен куб, внутри которого проведена диагональ d, являющаяся одновременно гипотенузой прямоугольного треугольника, заштрихованного на рисунке. Катетами треугольника служат рабро куба и диагональ квадрата, лежащего в основании (как указывалось ранее, длина диагонали равна 2а). Отсюда имеем
d=a+(2a), d=3a, d=3a.
Рассуждение, подобное этому, можно провести и для прямоугольного параллелепипеда с ребрами a, b, с и получить для диагонали выражение
d = a + b + c.

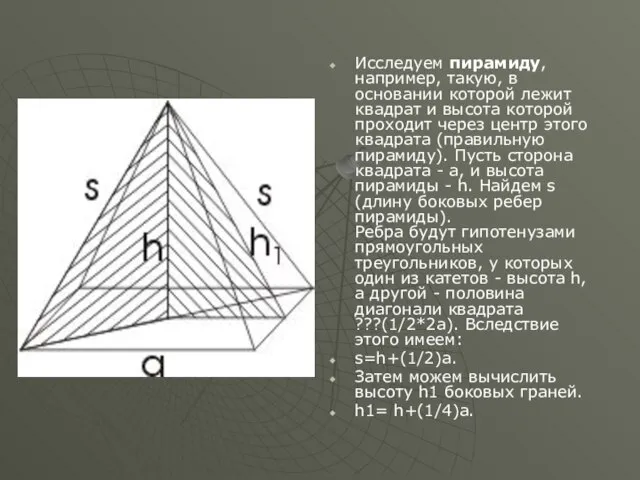
Исследуем пирамиду, например, такую, в основании которой лежит квадрат и высота которой проходит через центр этого квадрата (правильную пирамиду). Пусть сторона квадрата - а, и высота пирамиды - h. Найдем s (длину боковых ребер пирамиды).
Ребра будут гипотенузами прямоугольных треугольников, у которых один из катетов - высота h, а другой - половина диагонали квадрата ???(1/2*2a). Вследствие этого имеем:
s=h+(1/2)a.
Затем можем вычислить высоту h1 боковых граней.
h1= h+(1/4)a.

Применение теоремы на практике
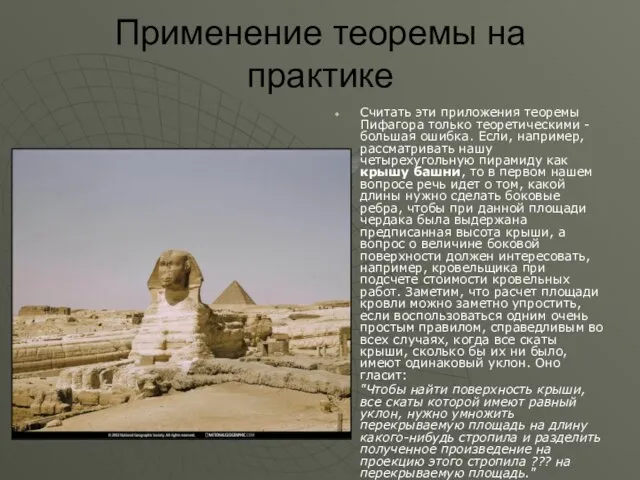
Считать эти приложения теоремы Пифагора только теоретическими - большая ошибка. Если, например, рассматривать нашу четырехугольную пирамиду как крышу башни, то в первом нашем вопросе речь идет о том, какой длины нужно сделать боковые ребра, чтобы при данной площади чердака была выдержана предписанная высота крыши, а вопрос о величине боковой поверхности должен интересовать, например, кровельщика при подсчете стоимости кровельных работ. Заметим, что расчет площади кровли можно заметно упростить, если воспользоваться одним очень простым правилом, справедливым во всех случаях, когда все скаты крыши, сколько бы их ни было, имеют одинаковый уклон. Оно гласит:
"Чтобы найти поверхность крыши, все скаты которой имеют равный уклон, нужно умножить перекрываемую площадь на длину какого-нибудь стропила и разделить полученное произведение на проекцию этого стропила ??? на перекрываемую площадь."

В зданиях готического и ромaнского стиля верхние части окон расчленяются каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон. На рисунке представлен простой пример такого окна в готическом стиле. Способ построения его очень прост: Из рисунка легко найти центры шести дуг окружностей, радиусы которых равны
ширине окна (b) для наружных дуг
половине ширины, (b/2) для внутренних дуг
Остается еще полная окружность, касающаяся четырех дугТ. к. она заключена между двумя концентрическими окружностями, то ее диаметр равен расстоянию между этими окружностями, т. е. b/2 и, следовательно, радиус равен b/4. А тогда становится ясным и положение ее центра. В рассмотренном примере радиусы находились без всяких затруднений. В других аналогичных примерах могут потребоватися вычисления; покажем, как применяется в таких задачах теорема Пифагора.

В романской архитектуре часто встречается мотив, представленный на рисунке. Если b по-прежнему обозначает ширину окна, то радиусы полуокружностей будут равны R = b / 2 и r = b / 4. Радиус p внутренней окружности можно вычислить из прямоугольного треугольника, изображенного на рис. пунктиром. Гипотенуза этого треугольника, проходящая через точку касания окружностей, равна b/4+p, один катет равен b/4, а другой b/2-p. По теореме Пифагора имеем:
(b/4+p)=( b/4)+( b/4-p)
или
b/16+ bp/2+p=b/16+b/4-bp+p,
откуда
bp/2=b/4-bp.
Разделив на b и приводя подобные члены, получим:
(3/2)p=b/4, p=b/6. У египтян была известна задача о лотосе.
Задача:"На глубине 12 футов растет лотос с 13-футовым стеблем. Определите, на какое расстояние цветок может отклониться от вертикали, проходящей через точку крепления стебля ко дну."