Применение теоремы Пифагора и пифагоровых троек для решения геометрических задач

Объект исследования:
Теорема Пифагора и пифагоровы тройки.
Предмет исследования:
Применение пифагоровых троек для быстрого решения геометрических задач.

Цель: Собрать сведения о пифагоровых тройках и их применения для решения практических задач курса геометрии и задач ЕГЭ типа В 4..
Гипотеза: Мы сможем найти способы быстрого решения геометрических задач и заданий ЕГЭ типа В 4, если будем знать приемы формирования пифагоровых триад и применять таблицы пифагоровых троек.

Задачи:
1. Показать уникальность открытия Пифагора и дать определение понятия пифагоровых троек .
2. Описать простые способы формирования пифагоровых троек.
3. Проанализировать возможности применения теоремы Пифагора, применения полученных знаний о пифагоровых тройках для их практического применения при решении задач.

Методы исследования:
методы теоретического исследования (анализ литературы, поиск источников);
анализ ряда задач учебника геометрии 7-9 класса;
методы эмпирического исследования (изучение опыта решения геометрических задач, нахождение рациональных способов).

Практическая значимость исследования определяется:
проведением исследования по проблеме формирования пифагоровых троек (описание простых способов)
описанием опыта применения знаний о пифагоровых тройках;
разработкой рекомендаций ученикам 8-11 класса при решении задач, материалы исследования могут быть использованы учениками и учителями при преподавании курса геометрии.

Глава 1. Теорема Пифагора и пифагоровы тройки
1.1 Биография Пифагора
Пифагор Самосский — древнегреческий философ и математик, создатель религиозно-философской школы пифагорейцев

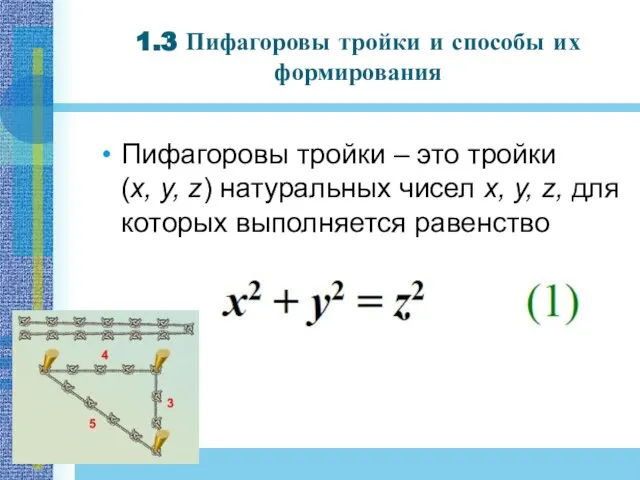
1.3 Пифагоровы тройки и способы их формирования
Пифагоровы тройки – это тройки
(x, y, z) натуральных чисел x, y, z, для которых выполняется равенство

Способ 1.
Обычно пользуются таким приемом подбора решений:
произвольные взаимно простые числа m и n, (m,n)=1, m >n одно из них четное, а другое нечетное, и формируют триаду
(m²- n²; 2mn; m²+ n²) (1)

Триаду (a, b, c) принято называть примитивной (основной),
если a и b – взаимно простые числа, т. е. (a, b) = 1
формула (m²- n²; 2mn; m²+ n²) дает все возможные примитивные триады.

2. Следующий приём возник из наблюдений над некоторыми свойствами триад.
а) Пусть первое число триады (длина одного катета) – нечетное, тогда, например, для триады
(3; 4; 5) наблюдаем: 3² =4+5,
(5; 12; 13) наблюдаем: 5² =12+13,
(7; 24; 25) - 7² =24+25 и т. д.

Эти наблюдения показывают приём подбора:
взять нечетное число , возвести его в квадрат и результат представить в виде суммы двух последовательных чисел; слагаемые будут вторым и третьим членами триады.
Пример: триада (13;84;85), 13² = 84+85
действительно 13² + 84² = 85².
А

б) пусть первое число триады – четное. Тогда, например, для триады (3; 4; 5) наблюдаем: 4=2(3+5), для триады (8;15; 17) 8=2(15+17) и т. д.
Наблюдения показывают прием подбора:
Взять число, кратное 4, его квадрат разделить на 2 и результат представить как сумму двух последовательных нечетных чисел; слагаемые будут вторым и третьим членами триады.
Пример: (16; 63; 65) 16 ²=2(63+65)
Б

Свойства пифагоровых троек
Свойство 1. Числа, входящие в простейшую пифагорову тройку, попарно взаимно просты.
Действительно, если два из них, например x и y имеют простой общий делитель p, то из равенства (1) следует, что на p делится и третье число z. Это противоречит тому, что тройка – простейшая.
Следствие. В простейшей пифагоровой тройке только одно число может быть чётным.
Свойство 2. В простейшей пифагоровой тройке числа x и y не могут быть одновременно нечётными.

Свойство 3.
Из данного пифагорова треугольника со сторонами (а, b, с) можно получить бесконечное множество подобных ему треугольников со сторонами (kа, kb, kс) , где k – произвольное натуральное число.

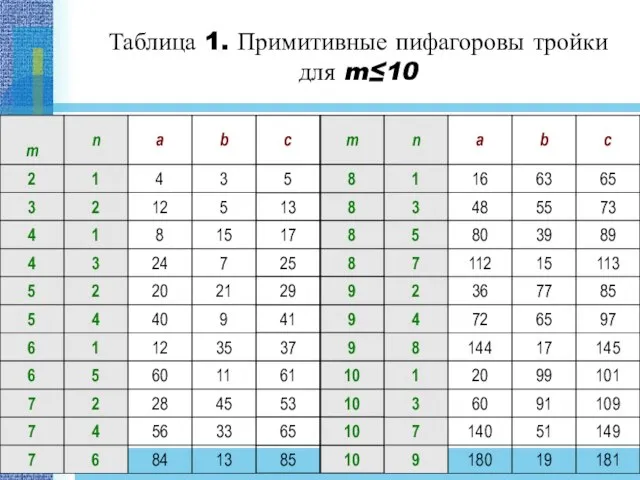
Таблица 1. Примитивные пифагоровы тройки для m≤10

Рассмотрим решение заданий, содержащихся в открытом банке заданий (адрес сайта http://mathege.ru/or/ege/ ).

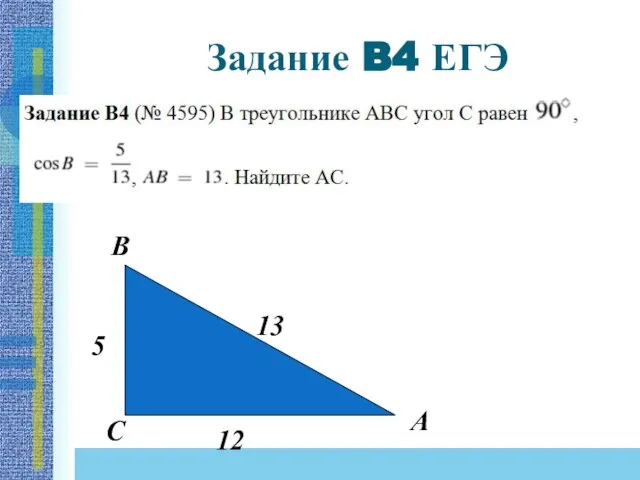
Задание B4 ЕГЭ
В
С
А
13
12
5

В этом задании сразу угадывается тройка (6, 8, 10). Остается только по рисунку определить отношение противолежащего катета углу А к прилежащему. tgA= 6/10= 0,6

Решение: Быстрый способ решения основан на понимании того факта, что синус угла это есть отношение сторон треугольника и следовательно стороны его можно задать как АВ = 8х, ВС (противолежащий катет) = 7х, АС = √15.
По теореме Пифагора,
решая уравнение найдем х = 1 и тогда гипотенуза АВ = 8.

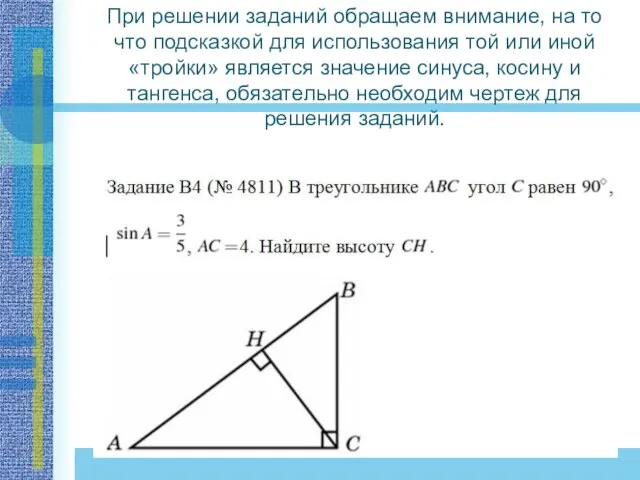
При решении заданий обращаем внимание, на то что подсказкой для использования той или иной «тройки» является значение синуса, косину и тангенса, обязательно необходим чертеж для решения заданий.

Заключение
Пифагоровы тройки находят прямое применение в проектировании множества вещей, окружающих нас в повседневной жизни. А умы учёных продолжают искать новые варианты доказательств теоремы Пифагора.