Признаки равенства треугольников

D
N
L
Назовите:
1) сторону, лежащую против угла N :
2) сторону, лежащую против угла NDL:
3) угол, лежащий против стороны DN:
4) угол, лежащий против стороны DL:
5) углы, прилежащие к стороне NL: и
Треугольник
Рис. 1

Первый признак равенства треугольников
M
F
N
L
O
Докажите, что OLF = OMN
Решение:
1) Рассмотрим OLF и :
а) OL = - по условию,
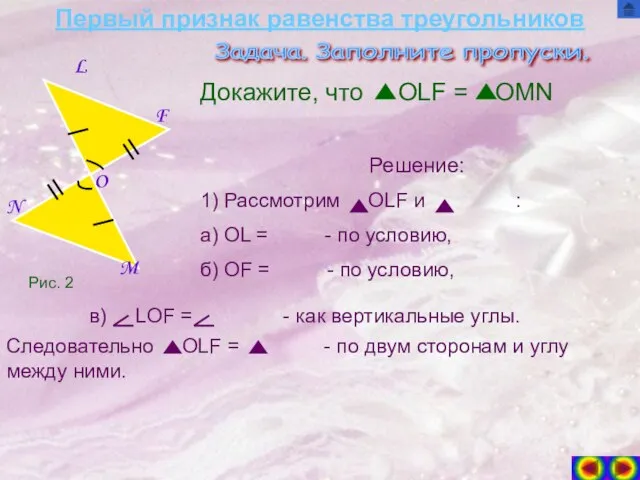
б) OF = - по условию,
Задача. Заполните пропуски.
Следовательно OLF = - по двум сторонам и углу между ними.
Рис. 2
в) LOF = - как вертикальные углы.

B
S
A
R
Задача. Заполните пропуски.
S
Докажите, что ARS = BRS
а) Сторона = - по условию.
б) Сторона = - общая сторона.
в) = - по условию.
г) Следовательно, ARS = - по двум
и углу .
2) Т. к. ASR= BSR, то соответственные стороны и углы равны, BR = AR = 18 см, BRS = ARS =
15˚
Решение:
1) Рассмотрим ARS и
Рис. 3

Второй признак равенства треугольников
Задача.
Докажите, что AXO = BZO
Решение:
A
X
B
Z
O
1) Рассмотрим BZO и
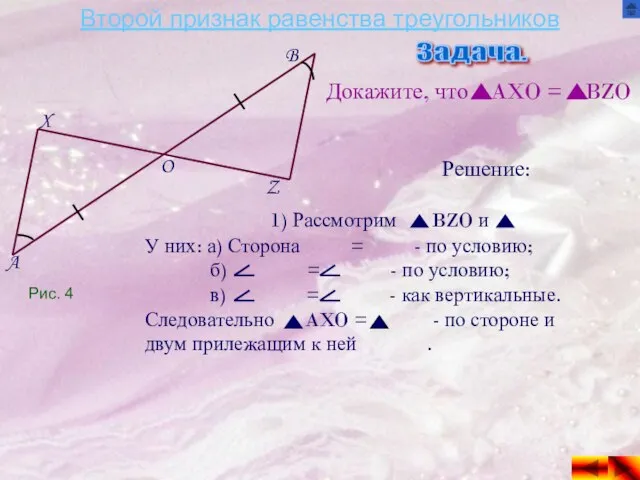
У них: а) Сторона = - по условию;
б) = - по условию;
в) = - как вертикальные.
Следовательно AXO = - по стороне и двум прилежащим к ней .
Рис. 4

Задача.
F
B
D
A
На рисунке 5 луч DF биссектриса угла ADF
а) Докажите, что ADF = BDF;
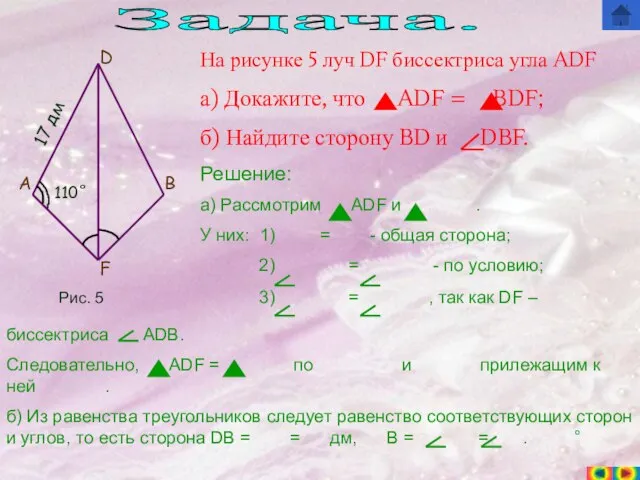
б) Найдите сторону BD и DBF.
Решение:
а) Рассмотрим ADF и .
У них: 1) = - общая сторона;
2) = - по условию;
3) = , так как DF –
17 дм
110˚
биссектриса ADB.
Следовательно, ADF = по и прилежащим к ней .
б) Из равенства треугольников следует равенство соответствующих сторон и углов, то есть сторона DB = = дм, B = = .
˚
Рис. 5

Третий признак равенства треугольников
A
N
B
C
108 ̊
а) Докажите, что CAN = BAN
б) Найдите ABN.
Решение:
а) Рассмотрим и BAN.
У них: 1) AC = - по условию;
2) CN = - по условию;
3) AN = AN – общая сторона.
Значит, CAN = - по трем .
б) Из равенства треугольников CAN и BAN следует равенство соответствующих углов, то есть ABN = = .
Рис. 6
˚

Рассмотрим треугольники ABC и DEF, у которых AB=DE, AC=DF, углы A и D равны (рис. 7). Докажем, что ABC = DEF.
Так как A = D, то треугольник ABC можно наложить на треугольник DEF так, что вершина A совместится с вершиной D, а стороны AB и AC наложатся соответственно на лучи DE и DF. Поскольку AB=DE, AC=DF, то сторона AB совместится со стороной DE, а сторона AC – со стороной DF; в частности, совместятся точки B и E, C и F. Следовательно, совместятся стороны BC и EF. Итак, треугольники ABC и DEF полностью совместятся, значит, они равны.
Рис. 7
C
A
B
D
E
F
Теорема
Доказательство
Теорема доказана.

Теорема
Рассмотрим треугольники ABC и DEF, у которых AB = DE, A = D, B = E (рис. 8). Докажем, что ABC= DEF.
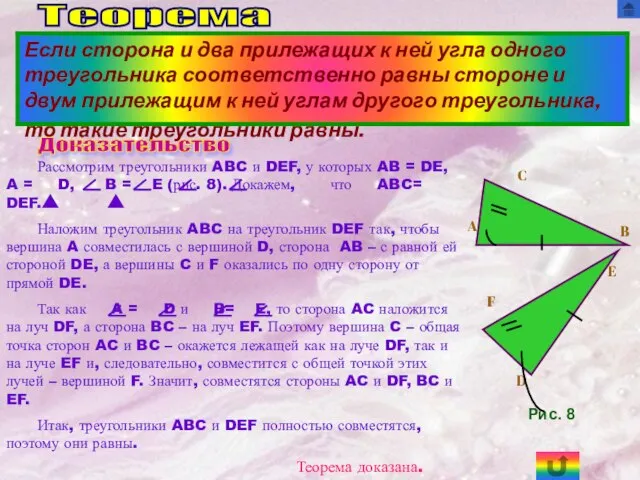
Наложим треугольник ABC на треугольник DEF так, чтобы вершина A совместилась с вершиной D, сторона AB – с равной ей стороной DE, а вершины C и F оказались по одну сторону от прямой DE.
Так как A = D и B= E, то сторона AC наложится на луч DF, а сторона BC – на луч EF. Поэтому вершина C – общая точка сторон AC и BC – окажется лежащей как на луче DF, так и на луче EF и, следовательно, совместится с общей точкой этих лучей – вершиной F. Значит, совместятся стороны AC и DF, BC и EF.
Итак, треугольники ABC и DEF полностью совместятся, поэтому они равны.
Теорема доказана.
C
A
B
Рис. 8
D
E
F
Доказательство