Содержание
- 2. Андрей Юрьевич Богомолов Российское хемометрическое общество European Molecular Biology Laboratory (EMBL) «Введение в анализ многомерных данных»
- 3. Тема лекции Многомерная калибровка Multivariate Calibration Анализ многомерных данных (Хемометрика) Multivariate Data Analysis (Chemometrics)
- 4. К вопросу о русской терминологии родной язык хемометрики - английский терминология за 30 лет устоялась: статьи,
- 5. Калибровка или градуировка? в русском языке – два сходных термина: «КАЛИБРОВКА (средств измерений) – совокупность операций,
- 6. Регрессия & Калибровка “Regression is an approach for relating two sets of variables to each other”
- 7. Регрессионный анализ линейная регрессия Y = XB + E МГК (PCA) – моделирование (X) регрессия –
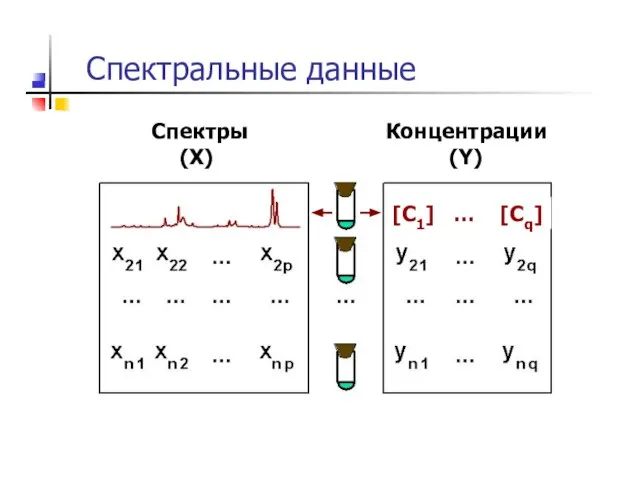
- 8. Спектральные данные Спектры (X) Концентрации (Y)
- 9. Для чего нужна калибровка? замена прямого измерения интересующего свойства, измерением другого, коррелирующего с первым такая потребность
- 10. Примеры из различных областей ХИМИЯ: калибровка – инструмент №1 количественного анализа БИОЛОГИЯ: непосредственный анализ может быть
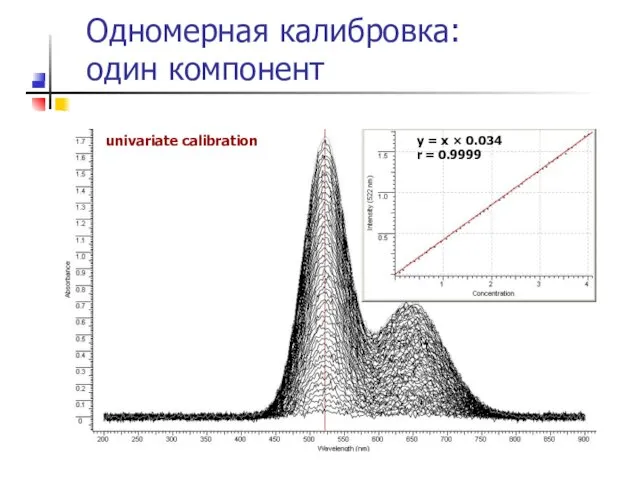
- 11. Одномерная калибровка: один компонент univariate calibration
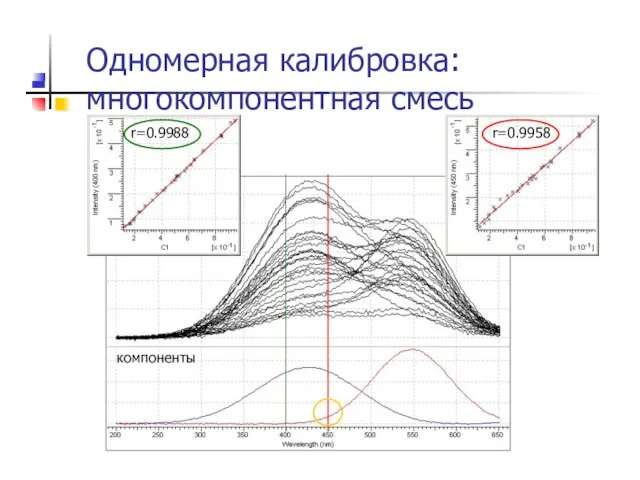
- 12. двухкомпонентная смесь Одномерная калибровка: многокомпонентная смесь компоненты
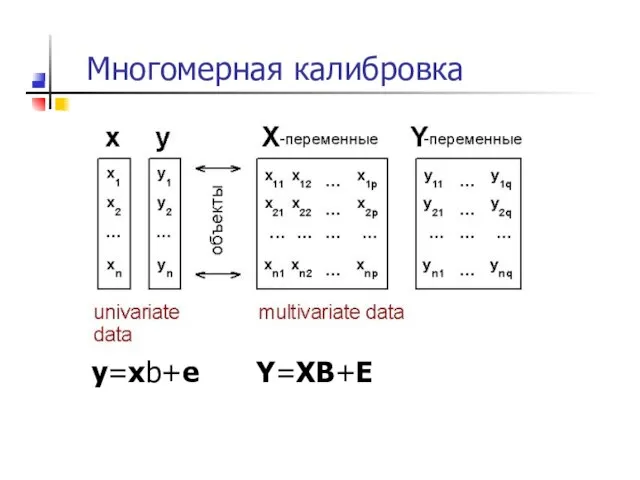
- 13. Многомерная калибровка y=xb+e Y=XB+E
- 14. Преимущества многомерной калибровки возможность анализировать несколько компонентов одновременно выигрыш в точности от усреднения при использования «избыточных»,
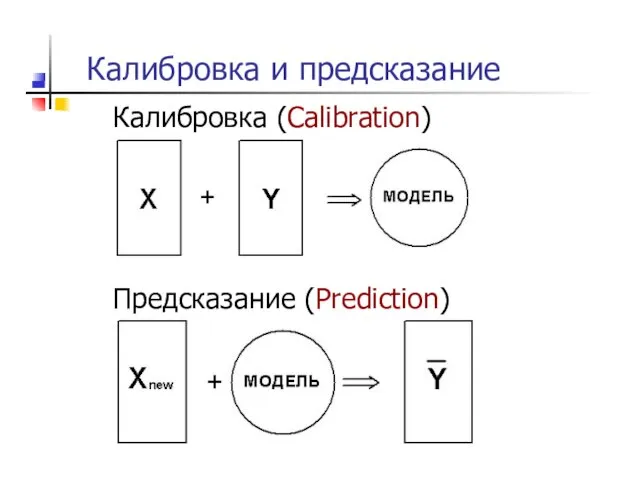
- 15. Калибровка и предсказание
- 16. Классические и инверсные методы Два основных подхода в многомерной калибровке: Классический МНК (Classical Least Squares, CLS)
- 17. Множественная линейная регрессия (МЛР) Multiple Linear Regression (MLR) Решение: b = (XT X)-1 XT y y=b0
- 18. Недостатки МЛР МЛР может не сработать, если: высока коллинеарность в X (спектры) неустойчивое решение для коллинеарных
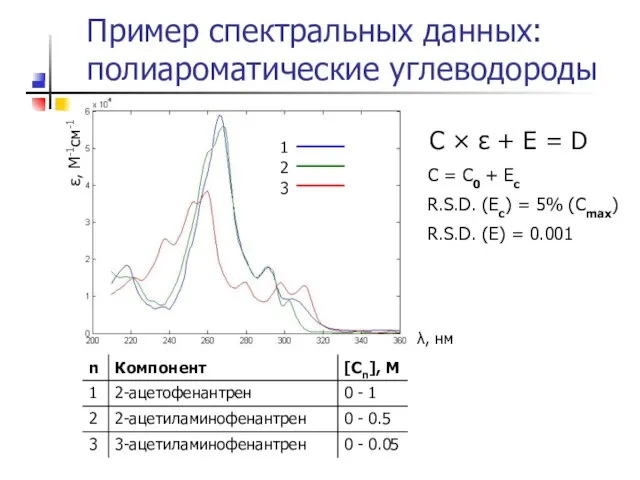
- 19. Пример спектральных данных: полиароматические углеводороды
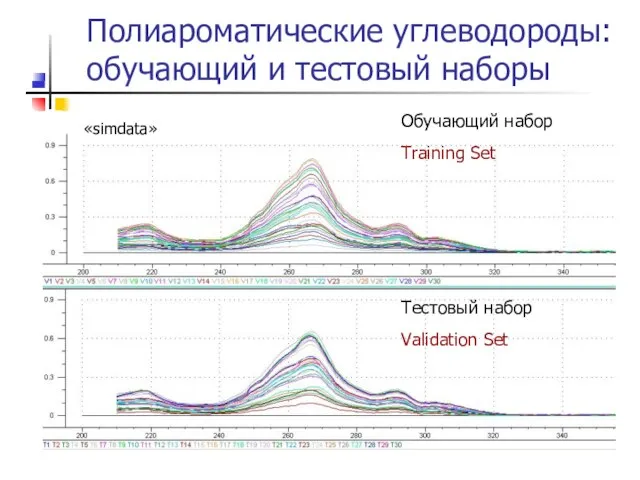
- 20. Полиароматические углеводороды: обучающий и тестовый наборы «simdata»
- 21. МЛР-калибровка (Simdata) точность МЛР-модели для [С3] (3-го компонента смеси ПАУ) неудовлетворительна
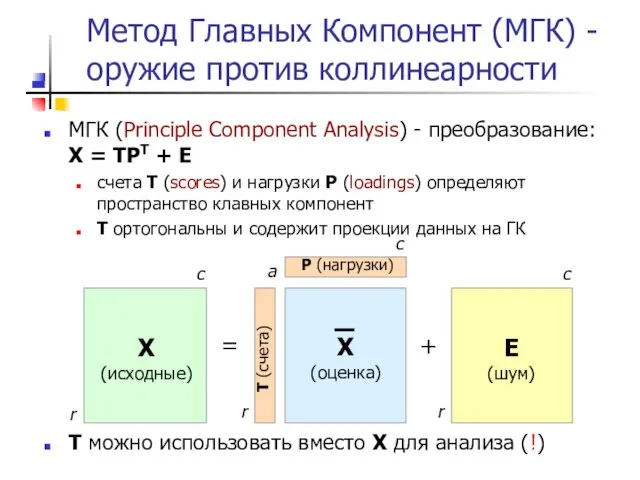
- 22. МГК (Principle Component Analysis) - преобразование: X = TPT + E счета T (scores) и нагрузки
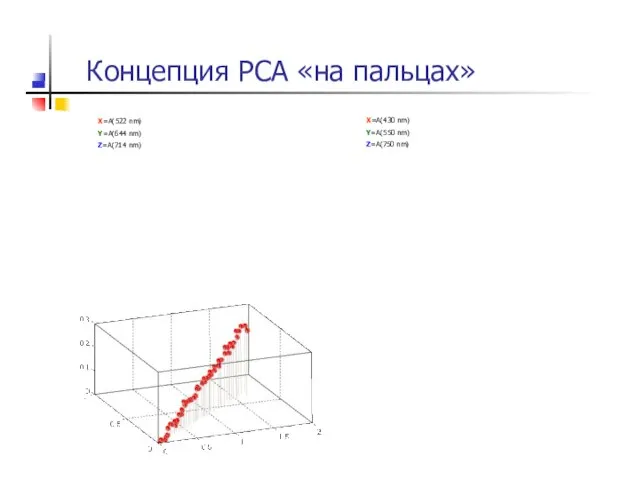
- 23. Концепция PCA «на пальцах» X=A(522 nm) Y=A(644 nm) Z=A(714 nm) X=A(430 nm) Y=A(550 nm) Z=A(750 nm)
- 24. МГК + МЛР = РГК! (PCA + MLR = PCR) МГК-счета (PCA scores) T можно использовать
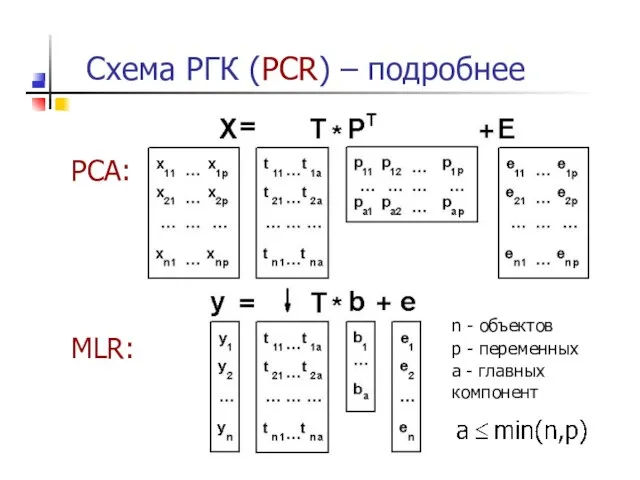
- 25. Схема РГК (PCR) – подробнее PCA: MLR:
- 26. Интерпретация РГК-модели интерпретация модели служит для изучения внутренней структуры данных: группы выбросы связь между X и
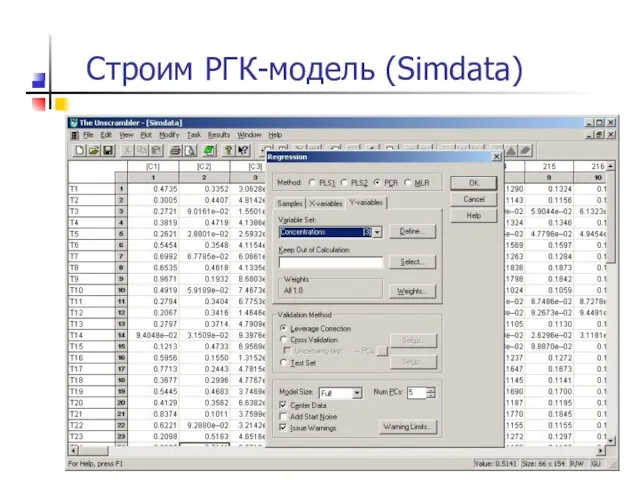
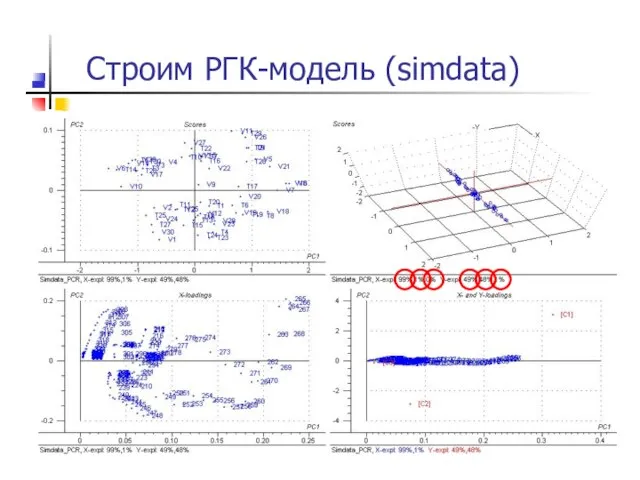
- 27. Строим РГК-модель (Simdata)
- 28. Строим РГК-модель (simdata)
- 29. Проверка (валидация) модели проверка (validation) модели служит для: определения размерности модели (числа ГК) оценки предсказательной способности
- 30. Среднеквадратичная ошибка предсказания (RMSEP) RMSEС = Root Mean Square Error of Calibration RMSEP = Root Mean
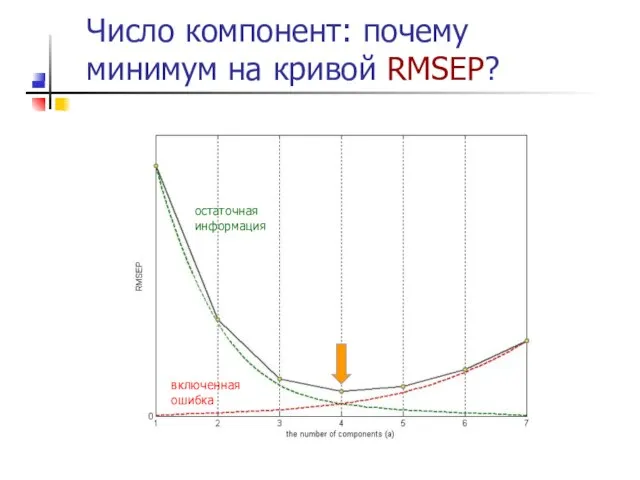
- 31. Число компонент: почему минимум на кривой RMSEP? включенная ошибка остаточная информация
- 32. Оценка числа компонент в РГК правильный выбор числа главных компонент (principle components, PC) - ключевая проблема
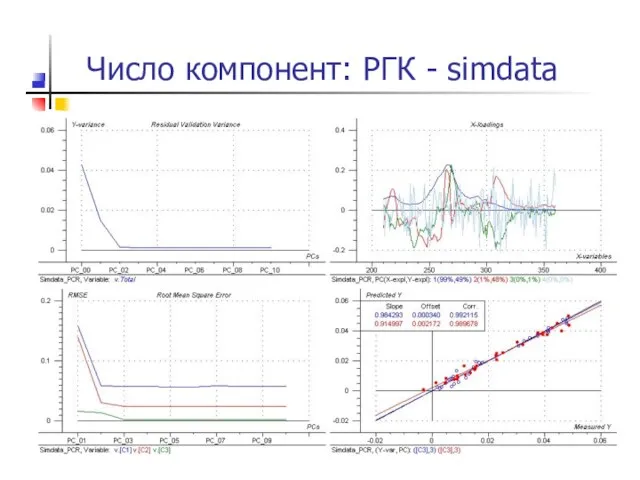
- 33. Число компонент: РГК - simdata
- 34. Число компонент: РГК - simdata
- 35. Оценка числа ГК в РГК: особенности число главных компонент (размерность модели) определяется в РГК (PCR) нуждами
- 36. Несовершенства РГК РГК (PCR) – мощный метод многомерной калибровки имеет безусловные преимущества перед MLR однако, не
- 37. Факторные пространства уравнение PCA имеет универсальный смысл: X = TPT + E преобразование называется факторной компрессией,
- 38. PLS – мощная альтернатива PCR Метод проекции на латентные структуры (ПЛС) и ПЛС-регрессия (ПЛС-Р) PLS =
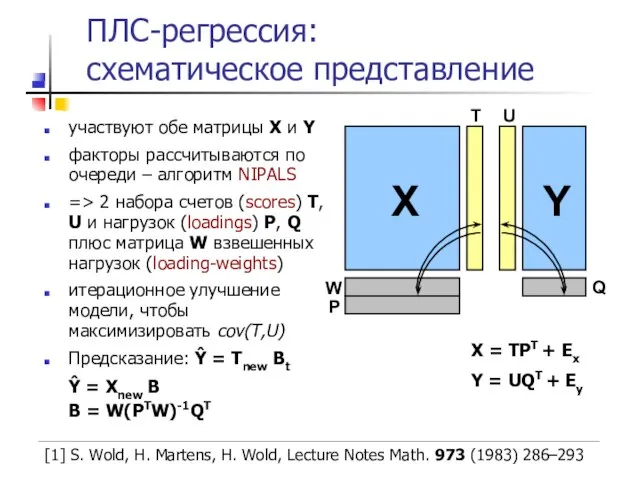
- 39. ПЛС-регрессия: схематическое представление участвуют обе матрицы X и Y факторы рассчитываются по очереди – алгоритм NIPALS
- 40. Две разновидности ПЛС: ПЛС1 и ПЛС2 существуют две популярных разновидности ПЛС: ПЛС1 (PLS1) и ПЛС2 (PLS2)
- 41. Основы алгоритма ПЛС ПЛС-декомпозиция производится алгоримом NIPALS NIPALS = Non-linear Iterative Partial Least Squares факторы находятся
- 42. NIPALS алгоритм для ПЛС2
- 43. NIPALS алгоритм для ПЛС1
- 44. NIPALS алгоритм для ПЛС1
- 45. ПЛС1 и ПЛС2 ПЛС1 моделирует только одну переменную y «за раз» ПЛС2 позволяет моделировать любую комбинацию
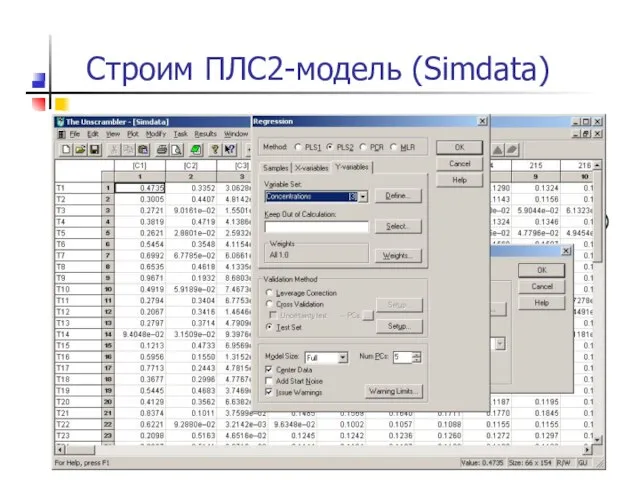
- 46. Строим ПЛС2-модель (Simdata)
- 47. Интерпретация модели служит для изучения внутренней структуры данных группы выбросы взаимовсвязи Сходство с РГК (PCR): X-счета
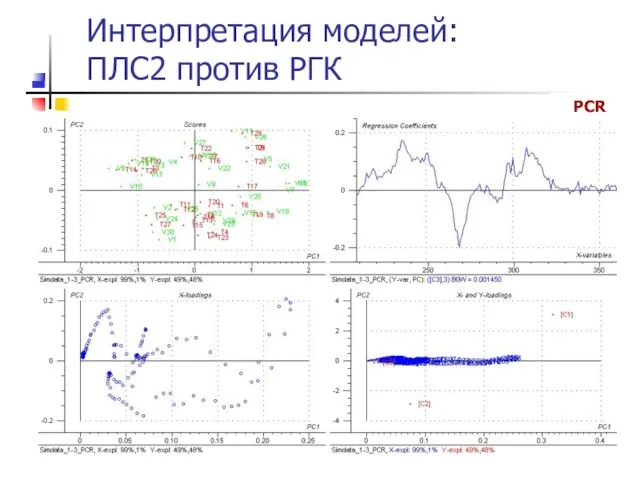
- 48. Интерпретация моделей: ПЛС2 против РГК PLS2
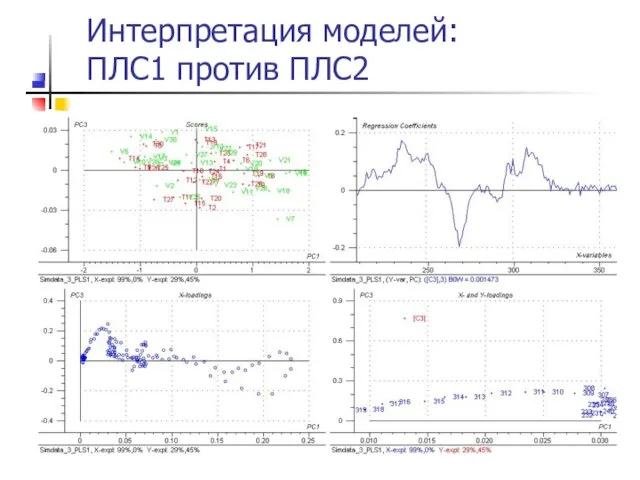
- 49. Интерпретация моделей: ПЛС1 против ПЛС2
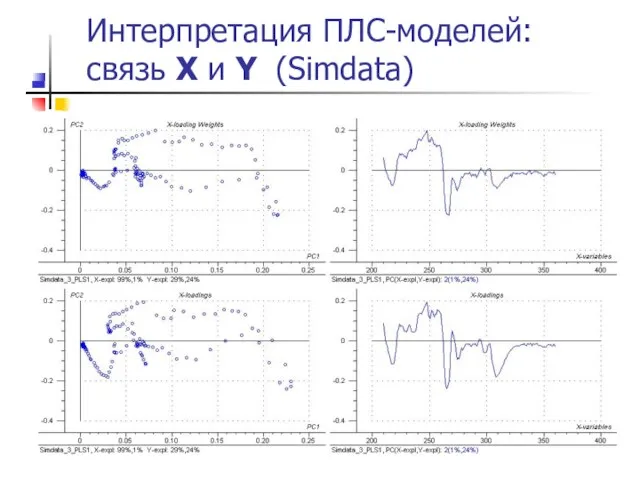
- 50. Интерпретация ПЛС-моделей: связь X и Y (Simdata)
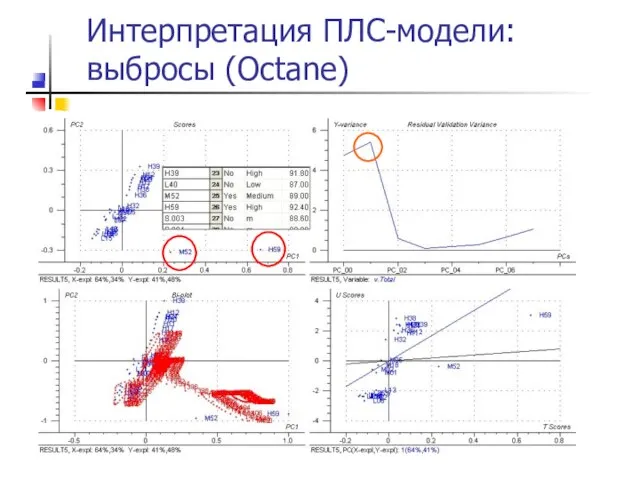
- 51. Интерпретация ПЛС-модели: выбросы (Octane)
- 52. Проверка регрессионных моделей Проверка (validation) модели преследует две основные цели: Определение оптимального числа компонент Меньше факторов
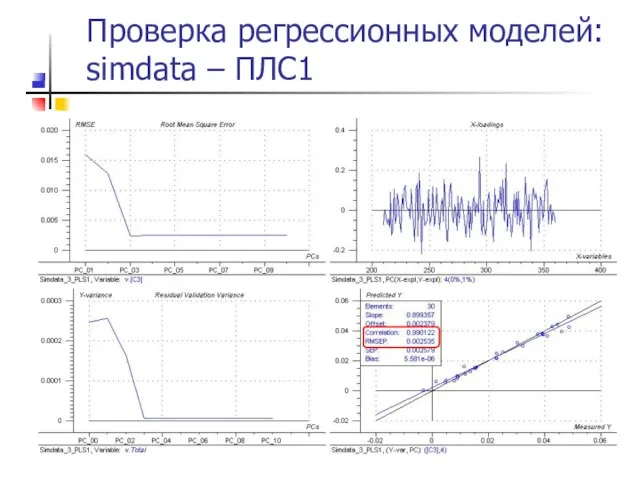
- 53. Проверка регрессионных моделей: simdata – ПЛС1
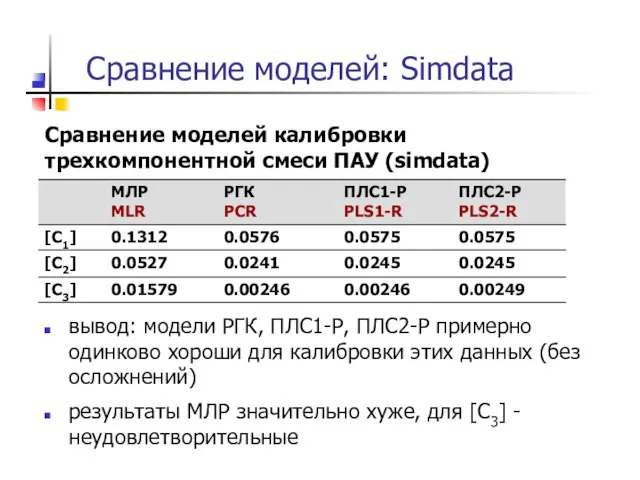
- 54. Сравнение моделей: Simdata Сравнение моделей калибровки трехкомпонентной смеси ПАУ (simdata) вывод: модели РГК, ПЛС1-Р, ПЛС2-Р примерно
- 55. Сравнение методов калибровки МЛР (MLR) плохо пригоден для спектроскопических данных РГК (PCR) имеет недостатки, но хорошо
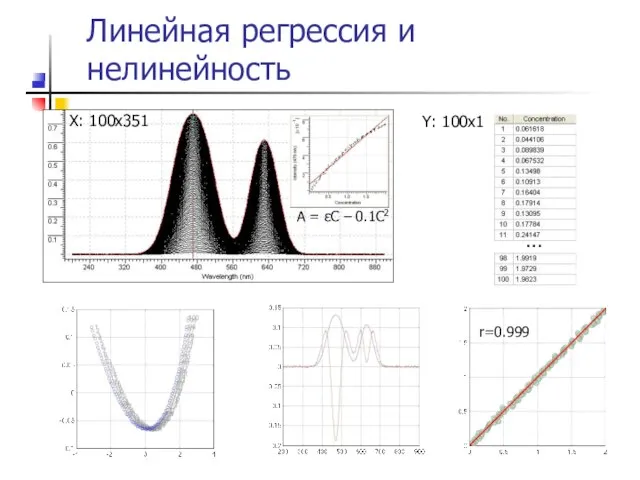
- 56. Линейная регрессия и нелинейность X: 100x351 r=0.999
- 57. Предсказание: диагностика соответствия новых образцов не все проблемы заканчиваются с построением калибровочной модели! возможность выявления образцов,
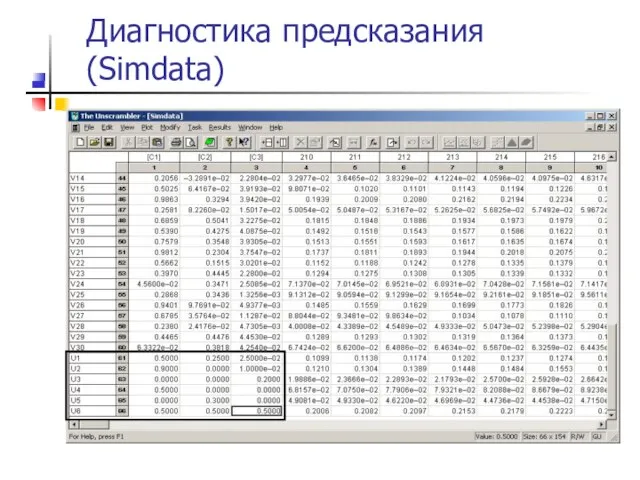
- 58. Диагностика предсказания (Simdata)
- 59. Диагностика предсказания: ПЛС1 - Simdata [C1] = 0 – 1 M [C2] = 0 – 0.5
- 60. Правила построения «хорошей» калибровки правильно приготовить (собрать) образцы визуально изучить данные, если необходимо, применить предварительную обработку
- 61. План семинара Пример 1. Концентрационная калибровка трехкомпонентной смеси ПАУ по спектрам в УФ-видимой области (искусственные данные).
- 62. Рекомендуемая литература Richard Kramer Chemometric Tchniques for Quantitative Analysis * Kim H. Esbensen Multivariate Data Analysis
- 63. Пример 1: Калибровка смеси ПАУ Файл Simdata Цель: выработка навыков калибровки с программой Unscrambler изучить наборы
- 64. Пример 2: Определение октанового числа бензина стр. 139, файл Octane Цель: работа с реальными данными, диагностика
- 66. Скачать презентацию












![МЛР-калибровка (Simdata) точность МЛР-модели для [С3] (3-го компонента смеси ПАУ) неудовлетворительна](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/401980/slide-20.jpg)




















![Диагностика предсказания: ПЛС1 - Simdata [C1] = 0 – 1 M [C2]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/401980/slide-58.jpg)





 Всероссийский конкурс лучших инновационных моделей семейных форм устройства детей-сирот и детей, оставшихся без попечения родите
Всероссийский конкурс лучших инновационных моделей семейных форм устройства детей-сирот и детей, оставшихся без попечения родите Казаковская сельская библиотека
Казаковская сельская библиотека ООО «Биологические источники энергии»
ООО «Биологические источники энергии» Необычные дома мира
Необычные дома мира Программа повышения энергоэффективности сетевого комплекса ОАО "Одинцовская электросеть" на основе привлечения средств без увел
Программа повышения энергоэффективности сетевого комплекса ОАО "Одинцовская электросеть" на основе привлечения средств без увел Презентация "Путешествие в мир Петрушки" - скачать презентации по МХК
Презентация "Путешествие в мир Петрушки" - скачать презентации по МХК Как гармонично совместить общественную работу и семью
Как гармонично совместить общественную работу и семью Интеллектуальный анализ данных
Интеллектуальный анализ данных Colosseum in Rome
Colosseum in Rome  Серьезные намерения. Готовность к браку и родительству
Серьезные намерения. Готовность к браку и родительству Семейные традиции
Семейные традиции Собрание
Собрание Высшее образование
Высшее образование Основные задачи клинического психолога
Основные задачи клинического психолога How to catch a mermaid by Adam Wallace
How to catch a mermaid by Adam Wallace Школьный электронный журнал
Школьный электронный журнал Пусть всегда будет солнце!
Пусть всегда будет солнце! Крестики - нолики
Крестики - нолики «Признаки делимости на 3 и на 9» УМК «Математика 5-6кл», авт. М.И. Башмаков.
«Признаки делимости на 3 и на 9» УМК «Математика 5-6кл», авт. М.И. Башмаков. Анатолий Георгиевич Алексин
Анатолий Георгиевич Алексин Основы менеджмента. Природа организации
Основы менеджмента. Природа организации d
d Нуклеиновые кислоты 9 класс
Нуклеиновые кислоты 9 класс Русская культура в произведениях русских классиков
Русская культура в произведениях русских классиков 20170112_urok_kaliningradskaya_0
20170112_urok_kaliningradskaya_0 Сварка швов
Сварка швов Энергетика как сфера бизнеса
Энергетика как сфера бизнеса Изменение фоновых картинок в презентациях PowerPoint и текстовом редакторе Word
Изменение фоновых картинок в презентациях PowerPoint и текстовом редакторе Word