Содержание
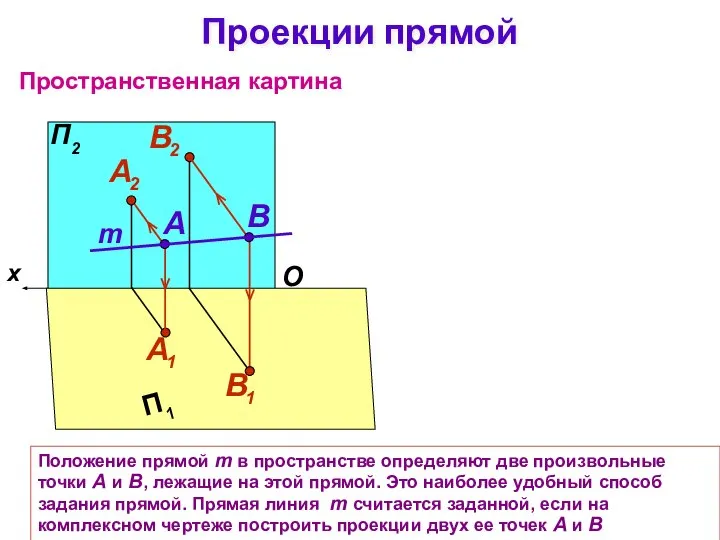
- 2. Положение прямой m в пространстве определяют две произвольные точки А и В, лежащие на этой прямой.
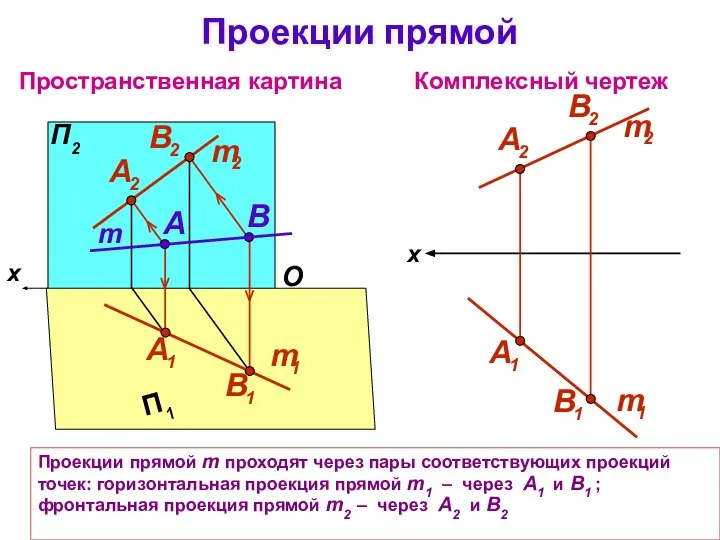
- 3. Проекции прямой m проходят через пары соответствующих проекций точек: горизонтальная проекция прямой m1 – через А1
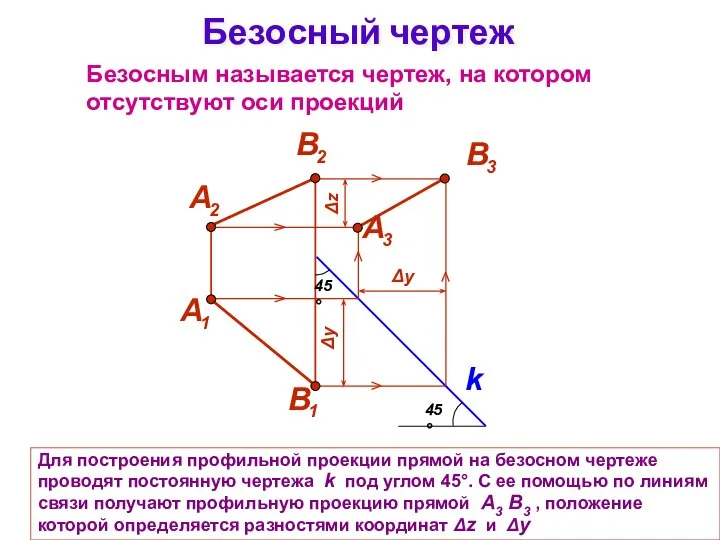
- 4. Для построения профильной проекции прямой на безосном чертеже проводят постоянную чертежа k под углом 45°. С
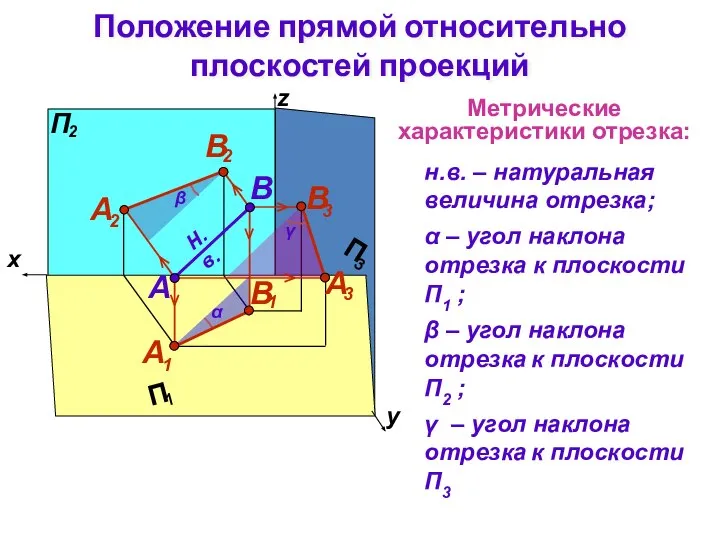
- 5. Метрические характеристики отрезка: н.в. – натуральная величина отрезка; α – угол наклона отрезка к плоcкости П1
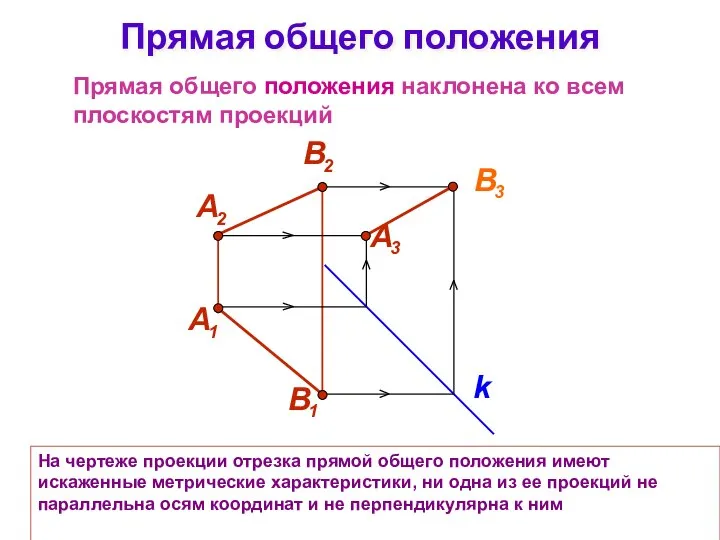
- 6. На чертеже проекции отрезка прямой общего положения имеют искаженные метрические характеристики, ни одна из ее проекций
- 7. У прямой частного положения на комплексном чертеже определяются натуральные величины каких-либо ее характеристик. Прямая уровня про-ецируется
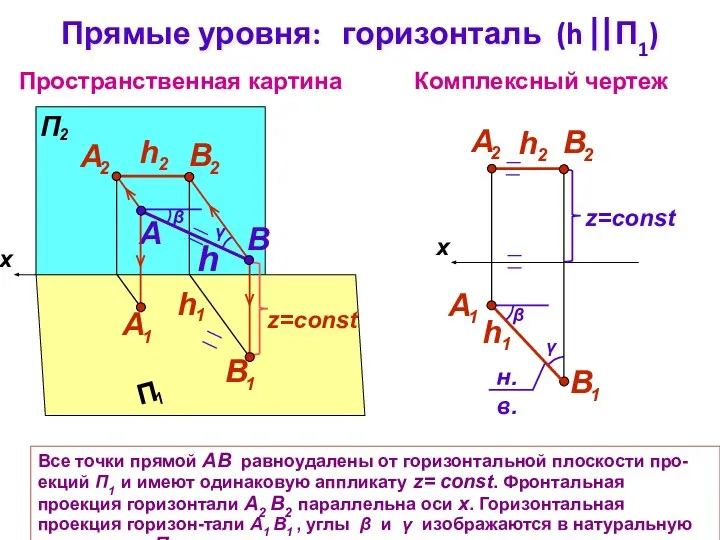
- 8. Все точки прямой АВ равноудалены от горизонтальной плоскости про-екций П1 и имеют одинаковую аппликату z= const.
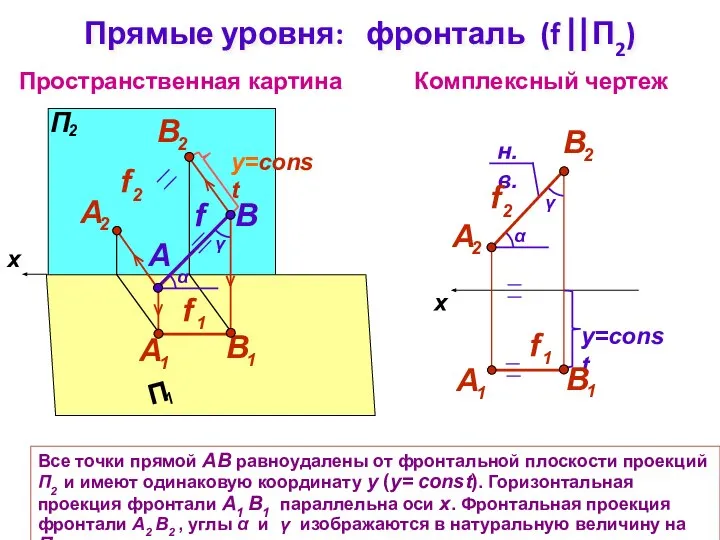
- 9. Пространственная картина Комплексный чертеж x B f Прямые уровня: фронталь (f ⎢⎢П2) A Все точки прямой
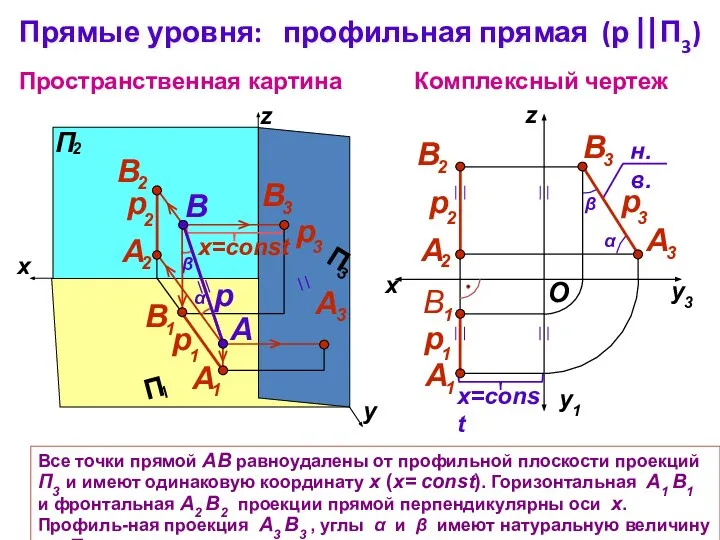
- 10. Все точки прямой АВ равноудалены от профильной плоскости проекций П3 и имеют одинаковую координату х (х=
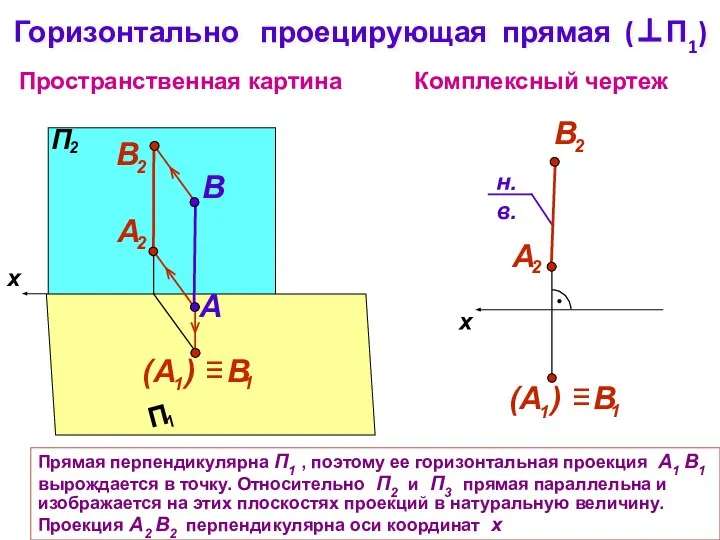
- 11. x Пространственная картина Комплексный чертеж A B Горизонтально проецирующая прямая (⊥П1) Прямая перпендикулярна П1 , поэтому
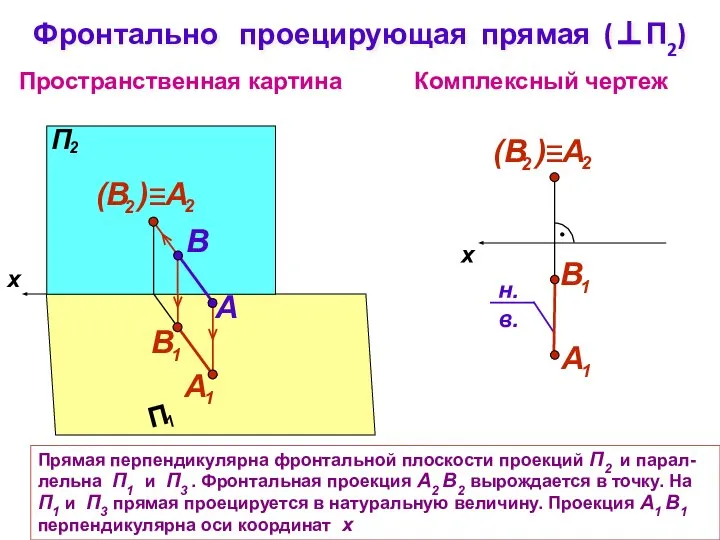
- 12. Прямая перпендикулярна фронтальной плоскости проекций П2 и парал-лельна П1 и П3 . Фронтальная проекция А2 В2
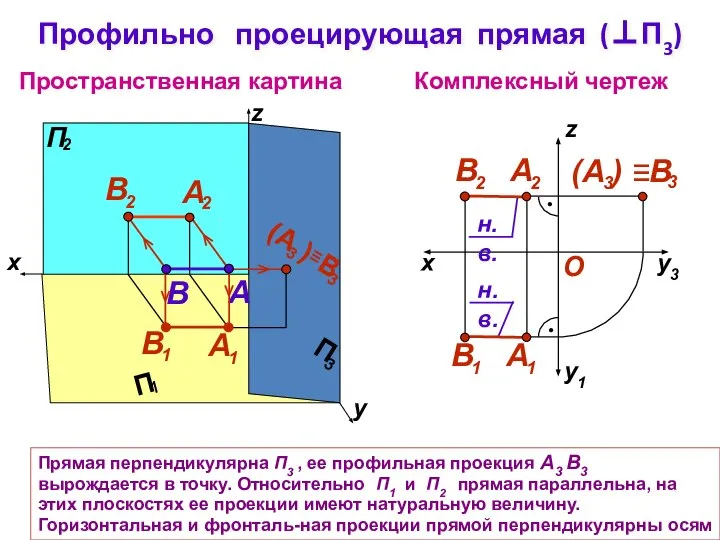
- 13. Прямая перпендикулярна П3 , ее профильная проекция А3 В3 вырождается в точку. Относительно П1 и П2
- 14. Преобразование чертежа прямой общего положения.
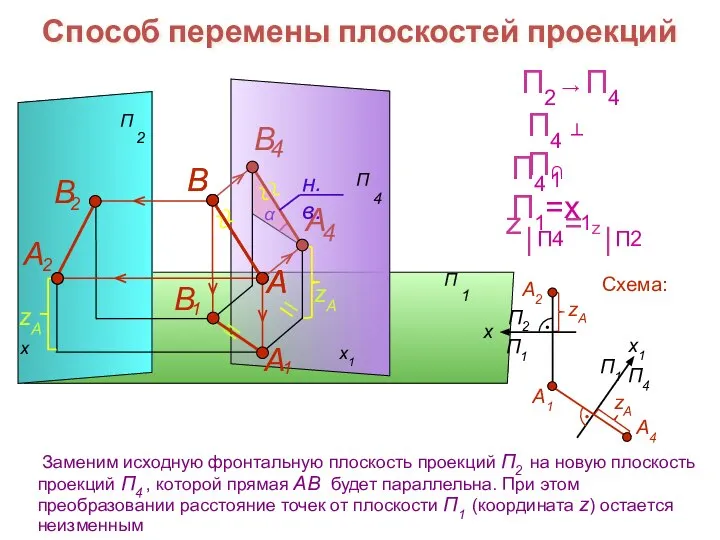
- 15. x1 Заменим исходную фронтальную плоскость проекций П2 на новую плоскость проекций П4 , которой прямая АВ
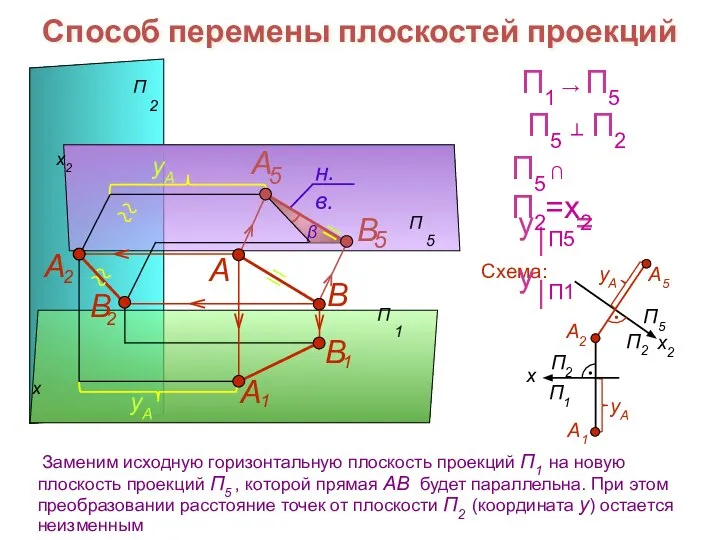
- 16. Способ перемены плоскостей проекций x x2 В А Схема: П1 → П5 y⎪П5= y⎪П1 П5 ⊥
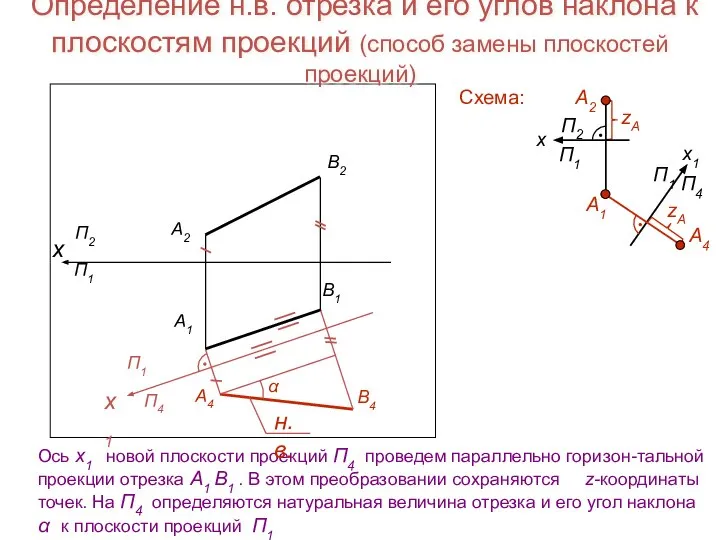
- 17. Определение н.в. отрезка и его углов наклона к плоскостям проекций (способ замены плоскостей проекций) Ось х1
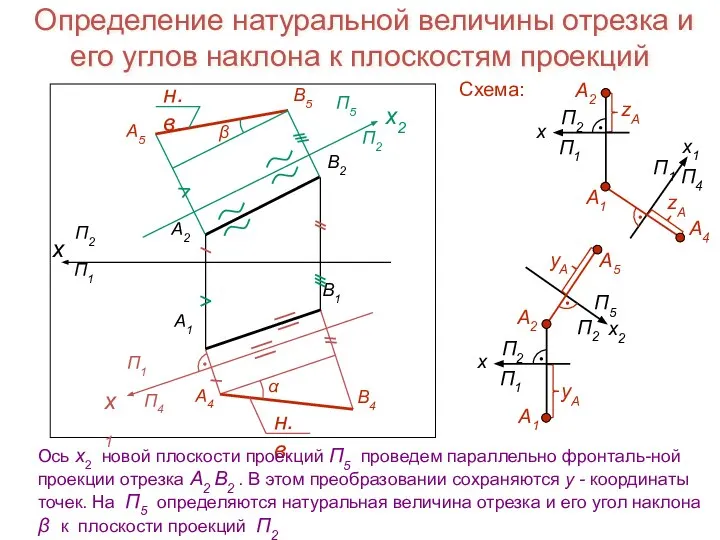
- 18. Определение натуральной величины отрезка и его углов наклона к плоскостям проекций x А1 B1 А2 B2
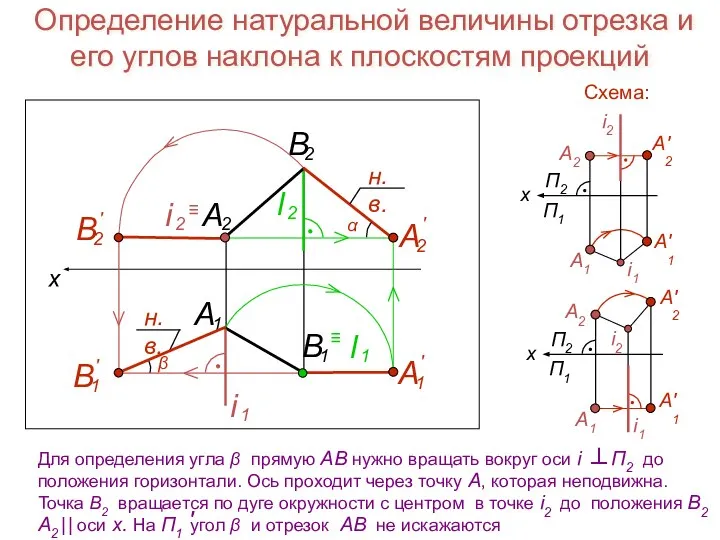
- 19. Определение натуральной величины отрезка и его углов наклона к плоскостям проекций
- 20. Определение натуральной величины отрезка и его углов наклона к плоскостям проекций
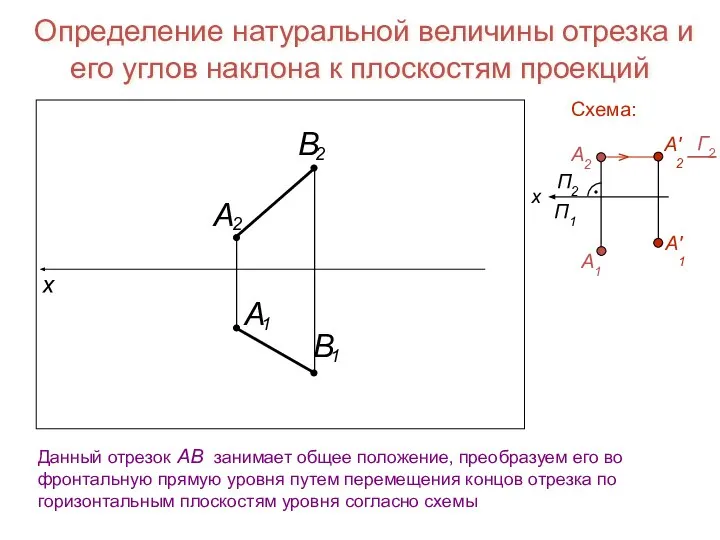
- 21. Определение натуральной величины отрезка и его углов наклона к плоскостям проекций Данный отрезок АВ занимает общее
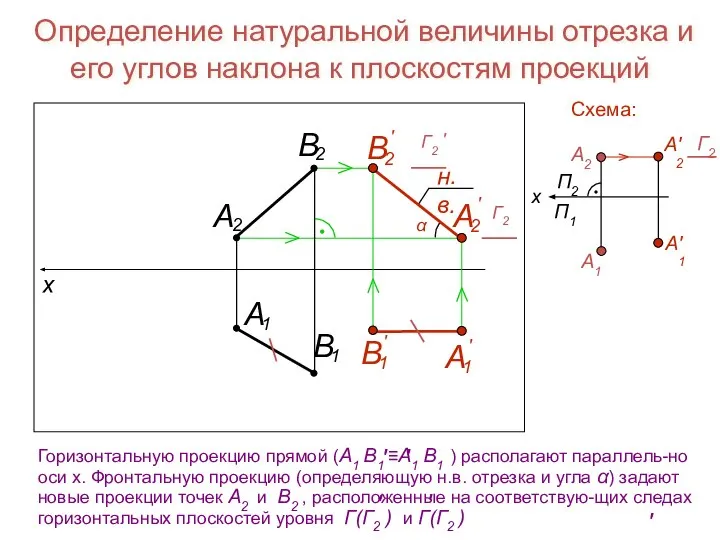
- 22. Определение натуральной величины отрезка и его углов наклона к плоскостям проекций
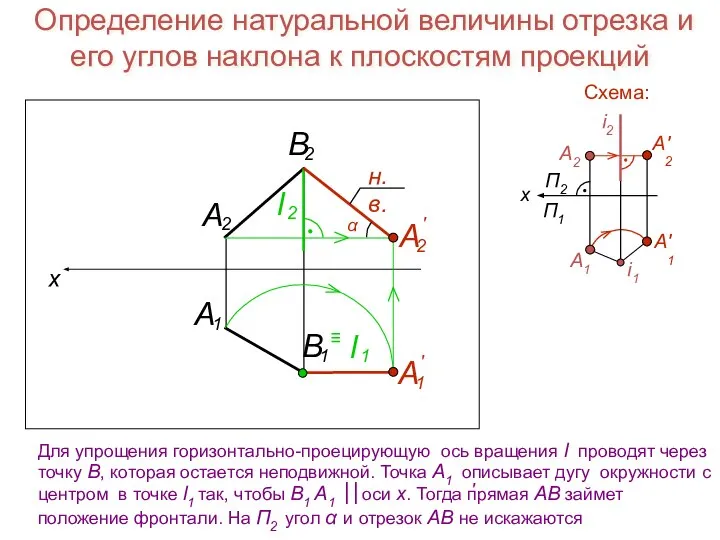
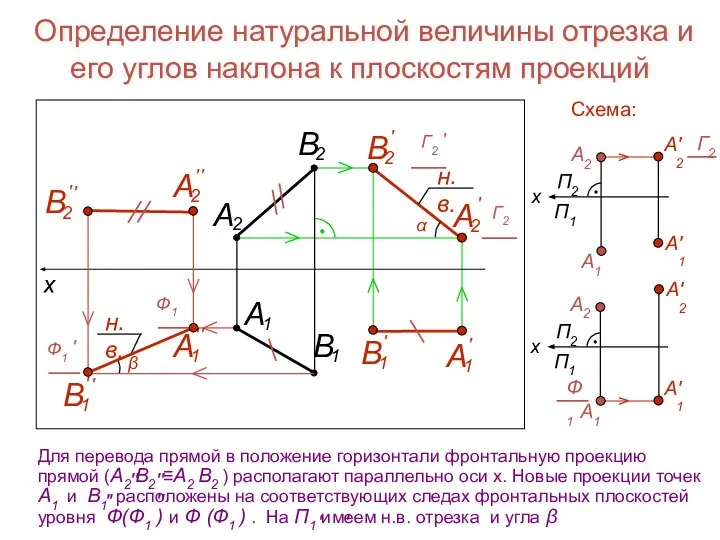
- 23. Определение натуральной величины отрезка и его углов наклона к плоскостям проекций Схема:
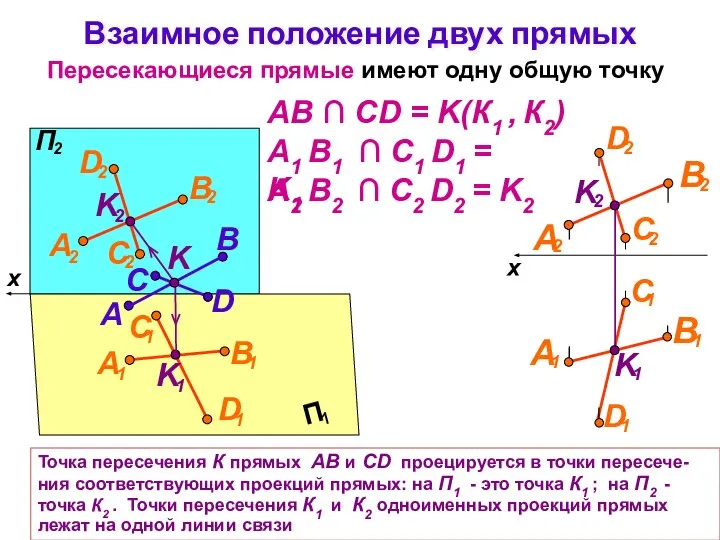
- 24. Взаимное положение двух прямых Пересекающиеся прямые имеют одну общую точку B A D C K x
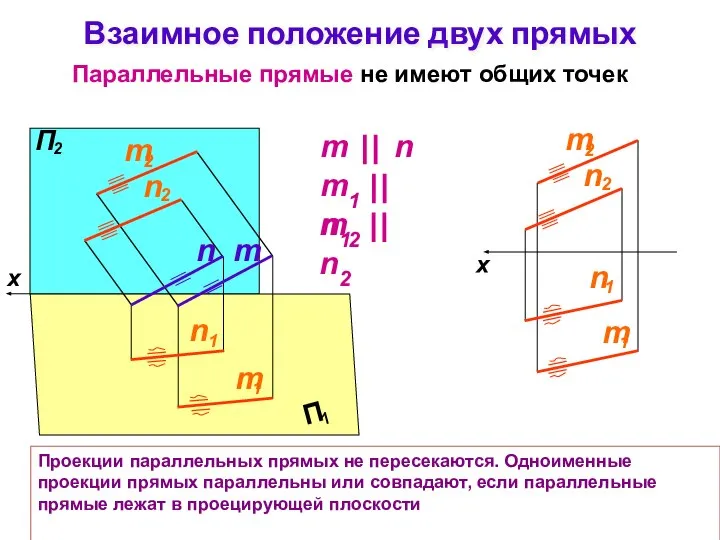
- 25. Взаимное положение двух прямых Параллельные прямые не имеют общих точек Проекции параллельных прямых не пересекаются. Одноименные
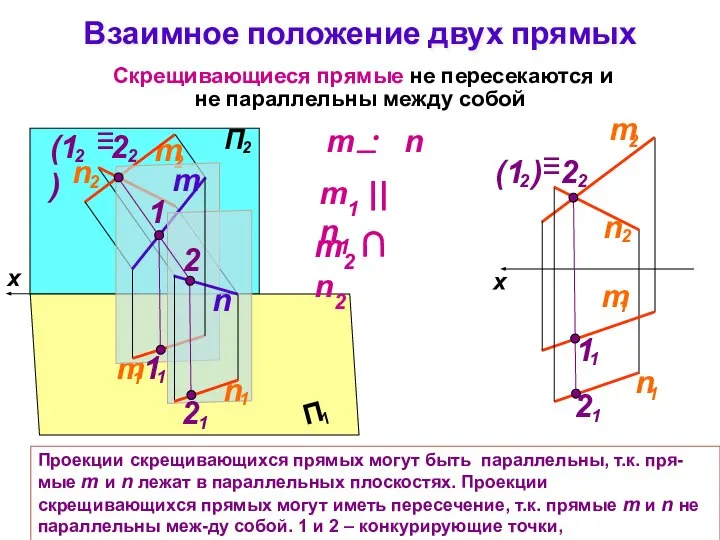
- 26. Взаимное положение двух прямых Скрещивающиеся прямые не пересекаются и не параллельны между собой Проекции скрещивающихся прямых
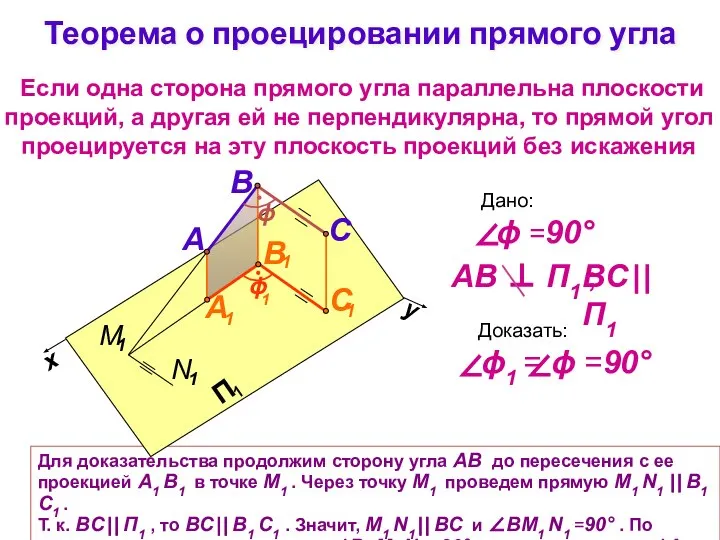
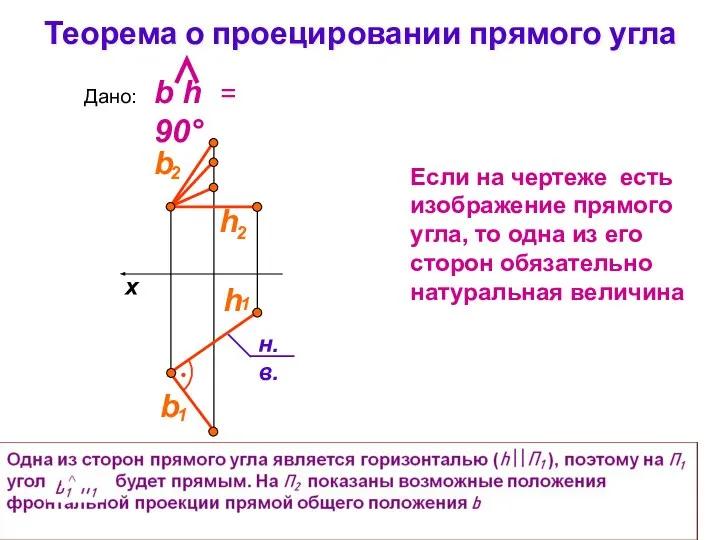
- 27. Теорема о проецировании прямого угла Если одна сторона прямого угла параллельна плоскости проекций, а другая ей
- 28. Теорема о проецировании прямого угла Если на чертеже есть изображение прямого угла, то одна из его
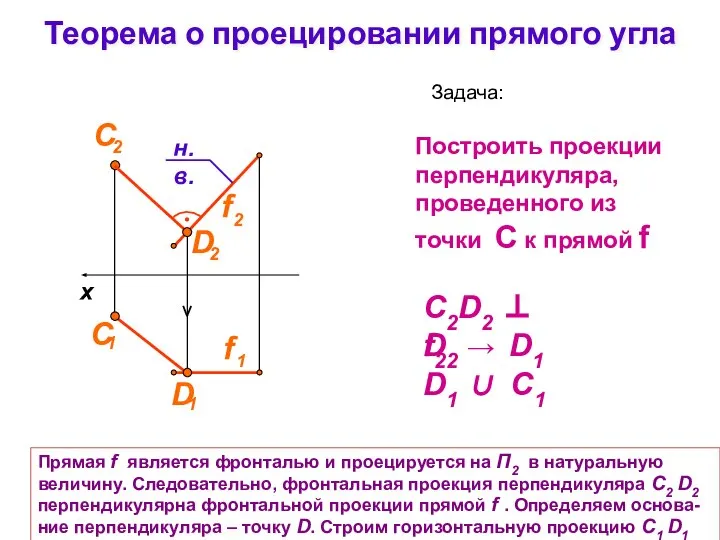
- 29. Теорема о проецировании прямого угла Задача: Построить проекции перпендикуляра, проведенного из точки С к прямой f
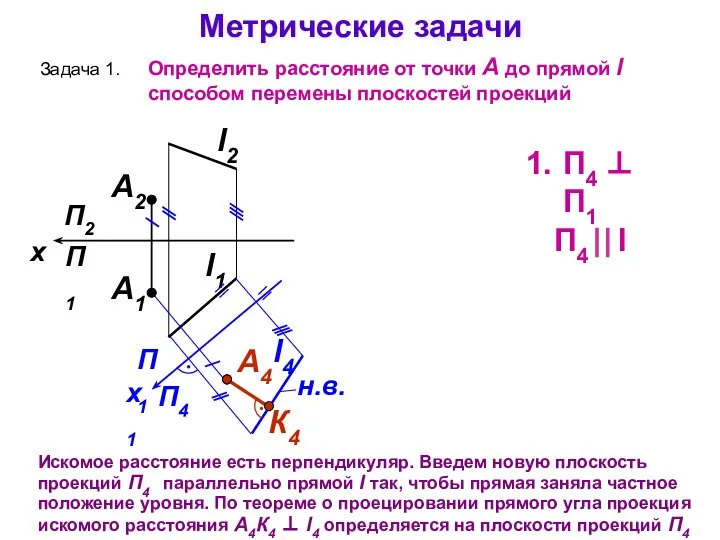
- 30. Метрические задачи Задача 1. Определить расстояние от точки А до прямой l способом перемены плоскостей проекций
- 32. Скачать презентацию


 Основные направления и потребители изделий с покрытиями Unibrait NicKel
Основные направления и потребители изделий с покрытиями Unibrait NicKel Постэмбриональный период развития организмов
Постэмбриональный период развития организмов Валуйский педагоги- ческий колледж ПРОЕКТНАЯ МЕТОДИКА ОБУЧЕНИЯ - педагогическая технология нового образования.
Валуйский педагоги- ческий колледж ПРОЕКТНАЯ МЕТОДИКА ОБУЧЕНИЯ - педагогическая технология нового образования. Безработица в Украине и Харьковской области
Безработица в Украине и Харьковской области Чем занимаются IT специалисты
Чем занимаются IT специалисты СТРАТЕГИЧЕСКОЕ ПЛАНИРОВАНИЕ И УПРАВЛЕНИЕ РАЗВИТИЕМ ТЕРРИТОРИАЛЬНОЙ ЕДИНИЦЫБАЙДАКОВ СЕРГЕЙ ЛЬВОВИЧЗАМЕСТИТЕЛЬ МЭРА МОСКВЫ
СТРАТЕГИЧЕСКОЕ ПЛАНИРОВАНИЕ И УПРАВЛЕНИЕ РАЗВИТИЕМ ТЕРРИТОРИАЛЬНОЙ ЕДИНИЦЫБАЙДАКОВ СЕРГЕЙ ЛЬВОВИЧЗАМЕСТИТЕЛЬ МЭРА МОСКВЫ  Проблема беженцев и военнопленных в современном мире
Проблема беженцев и военнопленных в современном мире ООО «Лафасад»
ООО «Лафасад» Правоохранительные и судебные органы. Контрольный вопрос по теме 7
Правоохранительные и судебные органы. Контрольный вопрос по теме 7 План счетов бухгалтерского учета
План счетов бухгалтерского учета Договірно-правова основа та ЕС
Договірно-правова основа та ЕС Нет долгим внедрениям - сразу начинаем использовать! Экономия времени руководства при внедрении снизу вверх Плюсы установки и из
Нет долгим внедрениям - сразу начинаем использовать! Экономия времени руководства при внедрении снизу вверх Плюсы установки и из Математический вечер для старшеклассников
Математический вечер для старшеклассников Об основных вопросах реализации Федерального закона от 27 июля 2010 года № 210-ФЗ «Об организации предоставления государственных и м
Об основных вопросах реализации Федерального закона от 27 июля 2010 года № 210-ФЗ «Об организации предоставления государственных и м Организация торгов
Организация торгов Развитие орфографической зоркости
Развитие орфографической зоркости Противовоздушная оборона
Противовоздушная оборона Meteozavisimost
Meteozavisimost инновационный проект
инновационный проект «И близких всех душа не позабудет…»
«И близких всех душа не позабудет…» ФИНАНСЫ ОРГАНИЗАЦИЙ
ФИНАНСЫ ОРГАНИЗАЦИЙ Строение человека
Строение человека Презентация на тему Обычаи, обряды и традиции русского народа
Презентация на тему Обычаи, обряды и традиции русского народа  ПОЛОЖЕНИЕо спонсорствепятого форума «Партнерство государства, бизнеса и гражданского общества при обеспечении информационной
ПОЛОЖЕНИЕо спонсорствепятого форума «Партнерство государства, бизнеса и гражданского общества при обеспечении информационной  Классификация органических соединений
Классификация органических соединений Проект Редизайн
Проект Редизайн Формула успеха
Формула успеха Войта-диагностика и Войта-терапия
Войта-диагностика и Войта-терапия