Производная и её геометрический смысл

ПРОИЗВОДНАЯ
Определение
Дифференцируемость
Производные элементарных функций
Геомерический смысл
Правила дифференцирования
Список литературы

ПРОИЗВОДНАЯ
Произво́дная — основное понятие дифференциального исчисления, характеризующее скорость изменения функции. Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует.

ДИФФЕРЕНЦИРУЕМОСТЬ
Производная f ‘( ) функции f в точке , будучи пределом, может не существовать или существовать и быть конечной или бесконечной. Функция f является дифференцируемой в точке тогда и только тогда, когда её производная в этой точке существует и конечна.

Список табличных производных основных элементарных функций.

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
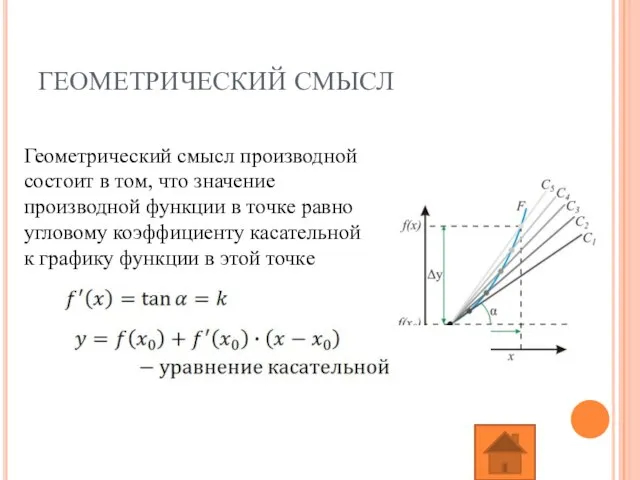
Геометрический смысл производной состоит в том, что значение производной функции в точке равно угловому коэффициенту касательной к графику функции в этой точке

ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
Производная произведения
Производная суммы
Производная частного
Сложная функция

ЗАДАНИЯ №1
Найти производную функции
?

ЗАДАНИЯ №2
Найти производную функции:
Найти f’(3) и f’(1), если
?

ЗАДАНИЯ №3
Найти производную функции
?

ЗАДАНИЯ №4
Наити угловой коэффициент касательной к графику финкции y=f(x) в точке сабциссой
?

ОТВЕТЫ
1)
2)
3)

ОТВЕТЫ
1)
2)
3)

ОТВЕТЫ
1)
2)
3)

ОТВЕТЫ