Производная и графики функций

Доказать, что функция монотонна на заданном промежутке:

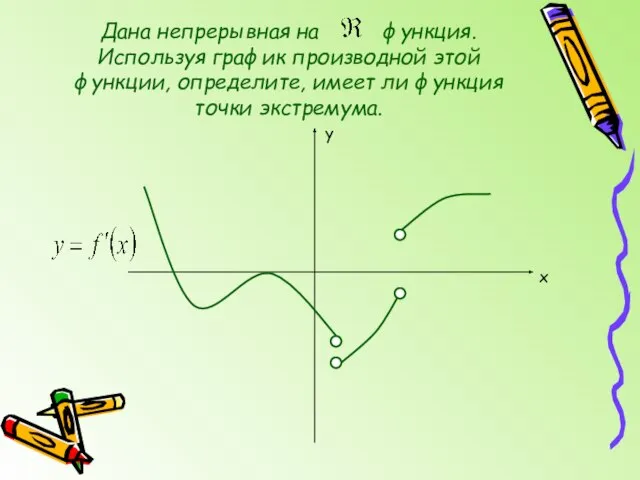
Дана непрерывная на функция. Используя график производной этой функции, определите, имеет ли функция точки экстремума.
y
x

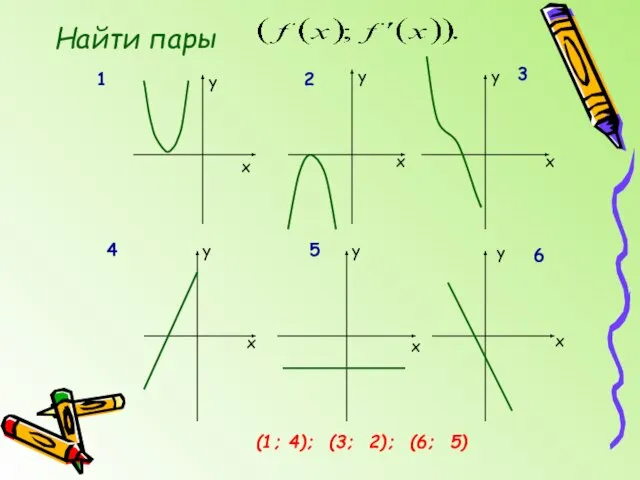
Найти пары
x
x
x
y
y
y
x
x
x
y
y
y
1
2
3
4
5
6
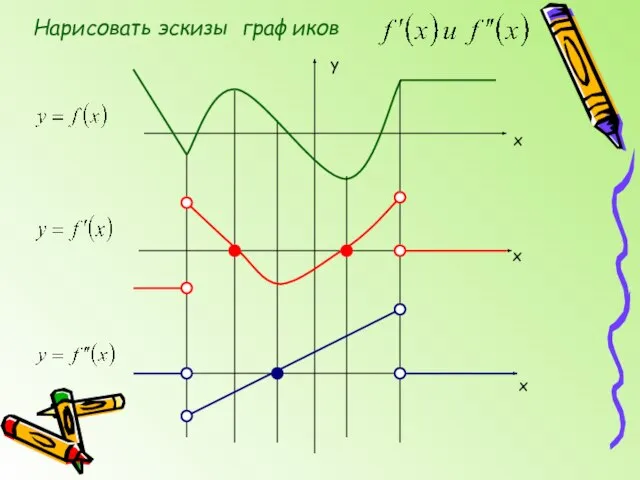
(1; 4); (3; 2); (6; 5)

Нарисовать эскизы графиков
y
x
x
x

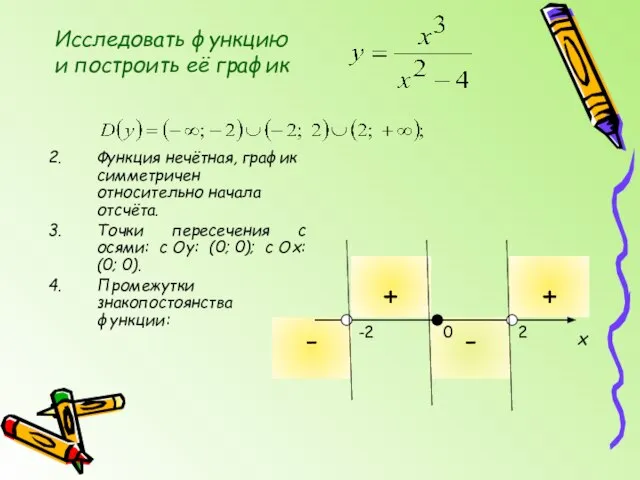
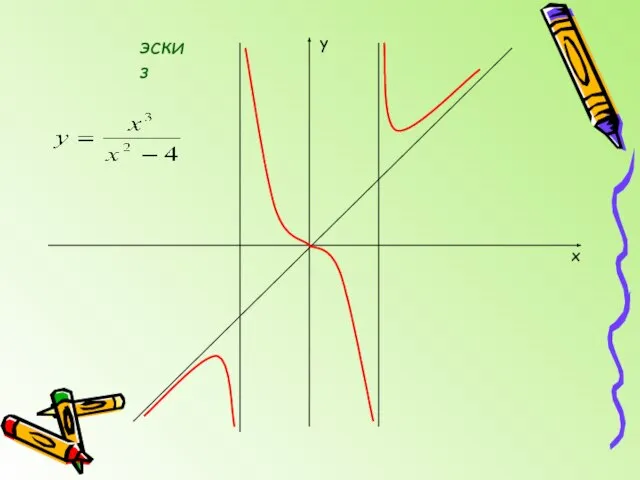
Исследовать функцию
и построить её график
Функция нечётная, график симметричен относительно начала отсчёта.
Точки пересечения с осями: с Оу: (0; 0); с Ох: (0; 0).
Промежутки знакопостоянства функции:
-2
2
0
х

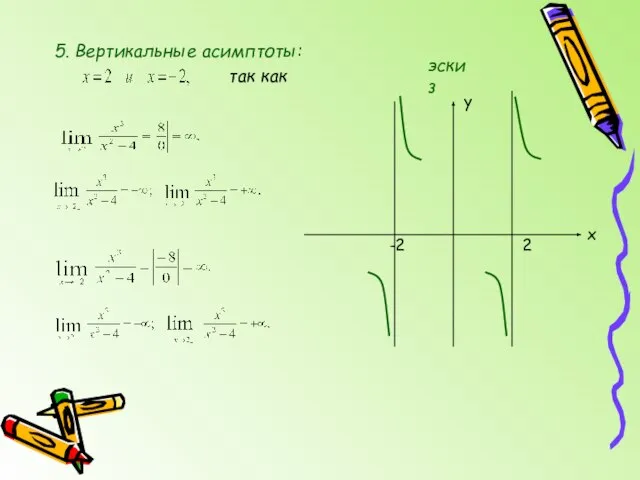
5. Вертикальные асимптоты:
так как
y
x
-2
2
эскиз

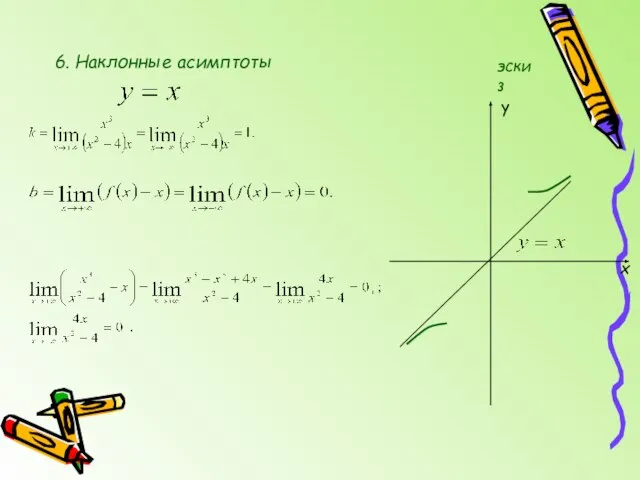
6. Наклонные асимптоты
x
y
эскиз

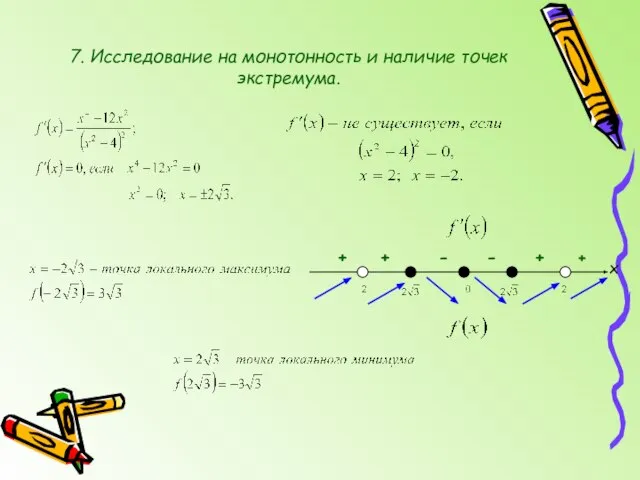
7. Исследование на монотонность и наличие точек экстремума.
х
+
+
-
-
+
+

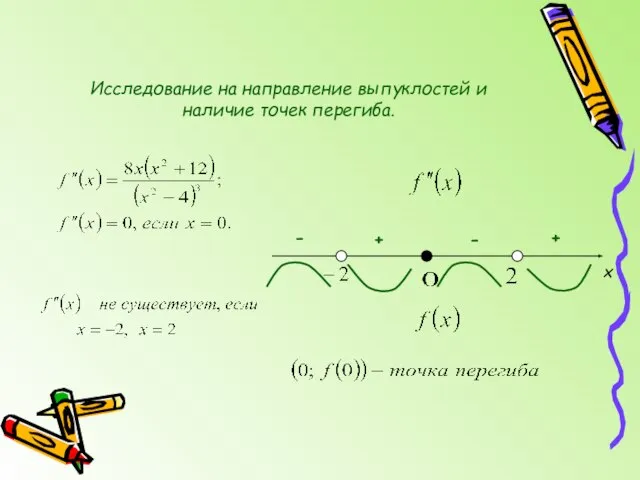
Исследование на направление выпуклостей и наличие точек перегиба.
х
+
-
+
-

y
x
эскиз