Простейшие задачи в координатах

Найти координаты векторов m = 3а, n = -в,
k= 0,5а + 2 в , если
а {2;4} , в{-3;2}
2. Даны векторы а {1;-2} и в {-3;2} , с {-2;-3} .
Найти х = 2 а -3 в + с.
3. Запишите разложение вектора х по неколлинеарным векторам i и j ,
4. Найти координаты вектора у , противоположного х .

САМОСТОЯТЕЛЬНАЯ РАБОТА
Даны векторы m {2;-1} , n {-3;4} , k {-1;-5} .
а) найти координаты вектора а = 3m +2n – k.
б) записать разложение вектора а по координатным векторам i и j

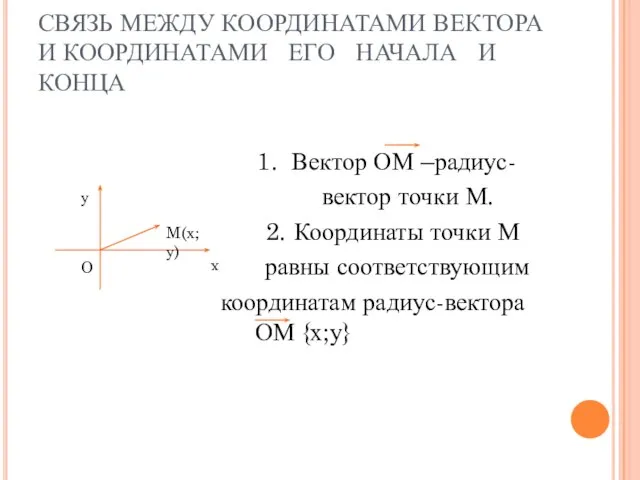
СВЯЗЬ МЕЖДУ КООРДИНАТАМИ ВЕКТОРА И КООРДИНАТАМИ ЕГО НАЧАЛА И КОНЦА
1. Вектор ОМ –радиус-
вектор точки М.
2. Координаты точки М
равны соответствующим
координатам радиус-вектора ОМ {х;у}
M(х;у)
O
х
у

.
КАЖДАЯ КООРДИНАТА ВЕКТОРА РАВНА РАЗНОСТИ СООТВЕТСТВУЮЩИХ КООРДИНАТ ЕГО КОНЦА И НАЧАЛА.
АВ= ОВ – ОА,
ОВ и ОА – радиус- векторы точек В и А.
ОВ {Х2 ; У2} ОА {Х1 ; У1}
АВ {Х2 ¯ Х1; У2 ¯У1 }
х
О
у
А (Х1 ; У1)
В (Х2 ; У2)