Психологические основы разработки стратегии обучения математике

План
Мышление и его виды.
2. Математическое мышление:
2.1. Сущность математического мышления;
2.2. Основные виды схем логического мышления.
3. Законы, уровни и этапы развития мышления.
4. Математические способности.

Мышление как преобразование информации
Мышление - активный процесс отражения объективного мира в сознание человека.
Мышление - опосредованное познание, осуществляемое путем чувственного восприятия объекта без прямого контакта с ним, путем мысленной переработки чувственных представлений.
Мышление позволяет устанавливать отношения и закономерности связей объектов, явлений и их свойства, что дает возможность предвидеть результаты наблюдаемых явлений и событий и своих собственных действий.

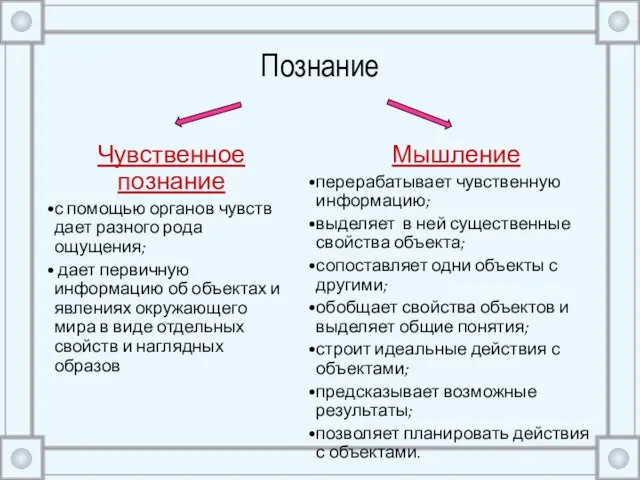
Познание
Чувственное познание
с помощью органов чувств дает разного рода ощущения;
дает первичную информацию об объектах и явлениях окружающего мира в виде отдельных свойств и наглядных образов
Мышление
перерабатывает чувственную информацию;
выделяет в ней существенные свойства объекта;
сопоставляет одни объекты с другими;
обобщает свойства объектов и выделяет общие понятия;
строит идеальные действия с объектами;
предсказывает возможные результаты;
позволяет планировать действия с объектами.

Мыслительные операции
анализ;
синтез;
сравнение;
абстрагирование;
обобщение;
специализация;
конкретизация;
классификация;
систематизация.

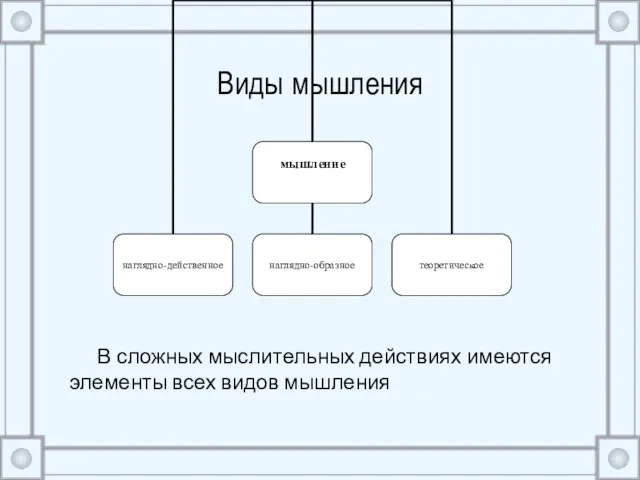
Виды мышления
В сложных мыслительных действиях имеются элементы всех видов мышления

Мышление и речь
Речь – материализованная оболочка мышления:
в речи мысль обретает форму, в речи результат мышления осознаётся человеком,
через речь результат мышления передаётся.
Развитие речи - одна из самых ведущих задач обучения.

Развитие мышления и обучение
Различные подходы к соотношению процессов развития и обучения:
Процесс развития мышления самостоятелен и независим от обучения (Ж.Пиаже);
Развитие зависит от обучения (Л.С. Выготский)
Положения лежащие в основе современных стратегий обучения:
Развитие мышления и обучение неотождествимы
Процесс умственного развития и процесс обучения связаны.
Развитие зависит от обучения, но эта зависимость не единственная, так как процесс развития зависит от социальных факторов, и от воспитания, и от характера обучения.

Зона актуального развития – такое состояние психических функций человека, при которых они могут проявляться в самостоятельной индивидуальной деятельности.
Зона ближайшего развития – такое состояние психических функций человека, при которых они проявляются и могут функционировать в коллективной деятельности или в деятельности под уменьшающимся руководством взрослых, но не могут самостоятельно проявляться.

Математическое мышление
Общие качества научного мышления, присущие математическому мышлению:
гибкость,
активность,
целенаправленность,
широта, глубина,
критичность и самокритичность,
ясность,
точность,
доказательность,
рациональность и т.п.
Более специфичные для математического стиля мышления качества:
(по А.Я. Хинчину)
доминирование логической схемы рассуждения,
лаконизм мышления: предельная скупость и суровая строгость мысли и ее изложения,
четкая расчлененность аргументации в рассуждениях,
скрупулезная точность символики

Математическое мышление
Основа мыслительных процессов – познавательные структуры или схемы, представляющие собой способ описания и хранения знаний в долговременной памяти человека
Современное математическое мышление характеризуется специфическими структурами, складывающимися в процессе изучения математики

Специфические для математического мышления структуры и схемы
Структуры, выступающие как модели математических объектов, как средства хранения математических знаний:
алгебраические структуры;
порядковые структуры,
топологические структуры
Структуры, выступающие как средства и методы научного познания:
логические схемы,
алгоритмические схемы,
комбинаторные схемы,
образно-геометрические
схемы

Логические схемы мышления – структуры, позволяющие из верных посылок (из суждений или утверждений) делать правильные (истинные) выводы, находить правильные следствия из имеющихся фактов.
Логические схемы проявляются:
в чёткой расчленённости и последовательности рассуждений,
в использовании в рассуждениях законов формальной логики,
в конструировании целого из заданных частей с заданными свойствами,
в использовании приёма доказательства «от противного»,
в использовании контрольных примеров как приёмов доказательства.

Алгоритмические схемы мышления – структуры, которые
позволяют применять известные алгоритмы, приёмы и методы,
спланировать некоторые действия, приводящие к результату (т.е. построить новый алгоритм),
позволяют доводить конечные планы до конца, выполняя конечную цепочку элементарных действий.
Компоненты алгоритмической культуры:
Интуитивное владение понятием алгоритма,
Владение средствами и методами описания алгоритмов.
Четкое владение алгоритмами школьного курса математики.
Умение строить и формулировать алгоритмы.
Понятие о программировании.

Комбинаторные схемы мышления – структуры, которые позволяют осуществлять организацию целенаправленного перебора определённым образом ограниченного круга возможностей и эффективное построение, перечисление и оптимизацию объектов, зависящих от сравнительно большого, но дискретного числа переменных.
Комбинаторные схемы применяются:
при решении текстовых задач арифметическим способом.
при решении многих задач тригонометрии.
при выборе рационального решения из нескольких имеющихся и т.п.

Образно геометрические схемы мышления – структуры, позволяющие интерпретировать абстрактные математические объекты, выражения и отношения, оперировать наглядными схемами, образами и представлениями.
Геометрическое мышление в своей основе является разновидностью чувственного и образного мышления.
Высшей ступенью развития геометрического мышления является пространственное мышление, которое характеризуется умением мысленно конструировать пространственные образы или схематические конструкции для изучаемых объектов, и умением выполнять с этими конструкциями мыслительные операции.

Законы развития мышления
Развитие мышления – частный вид общего процесса развития
Развитие математического развития подчиняется законам:
Структурной дифференциации – закону развития от общего к частному и от целого к частям;
Структурной интеграции – закону развития от простого к сложному
В специфических законах развития мышления прослеживается действие всех универсальных законов развития и законов теории познания

Уровни развития математического мышления
( по А.А. Столяру)
1. Уровень конкретных множеств (от 6-7 лет до 8-9 лет).
2. Уровень конкретных математических структур
(с 8-9 лет до 11-12 лет).
3. Уровень синтеза конкретных структур
(от 11-12 лет до 15 лет).
4. Уровень содержательных структур
(с 15 лет до 18-19 лет).
5. Уровень абстрактных структур
(с 19-20 лет до – за пределами учебных заведений).

Теория поэтапного формирования умственных действий
(Л.С.Выготский, П.А.Гальперин, Н.Ф.Талызина)
Основные идеи:
существует принципиальная общность внутренней и внешней деятельности человека,
умственное развитие происходит путём интериоризации, т.е. поэтапным переходом материальной деятельности с конкретными объектами во внутренний умственный план.

Этапы формирования умственных действий
1.Этап мотивации.
2.Этап создания ориентированной основы деятельности.
3.Этап материализованного (материального) действия.
4.Этап внешней речи (устной или письменной).
5.Этап внутренней речи.
6.Этап автоматизированного действия.

Общая характеристика этапов формирования умственных действий
Первый этап предполагает актуализацию соответствующей мотивации учащегося, предварительное ознакомление с целью действия, так как только в том случае, когда цель задания совпадает с мотивом, можно считать действия деятельностью.
Второй этап связан с осознанием схемы ориентировочной основы деятельности (действия).
Выделяют три типа такой основы:
• неполная система ориентировок в готовом виде, по образцу, необходимая для оперативного исполнения;
• полная ориентировочная основа действия в готовом виде;
• ориентировочная основа действия в обобщенном виде.

Общая характеристика этапов формирования умственных действий
Третий этап - выполнение действия во внешней форме - материальной или материализованной, т.е. с помощью каких-либо моделей, схем, чертежей и т.п.
Эти действия включают не только ориентационные, но и исполнительные и контрольные функции. От учащихся требуется проговаривание вслух сообщений о совершаемых операциях и их особенностях.
Четвертый этап предполагает внешнюю речь, когда действие подвергается дальнейшему обобщению благодаря речевому (устному или письменному) оформлению и отрыву от материализованных средств.

Общая характеристика этапов формирования умственных действий
Пятый этап - этап внутренней речи, на котором действие приобретает умственную форму, но при этом сохраняется осознанный контроль за его выполнением.
Шестой этап связан с выполнением действия в умственном плане (интериоризация действия), действие выполняется на уровне подсознания, т.е. переходит в мысль.

Математические способности
Способности – индивидуально-психические особенности человека, отвечающие требованиям какой-либо деятельности и обеспечивающие при всех равных условиях высокий уровень достижений.
Способности не сводятся к знаниям, умениям и навыкам

Подходы к природе способностей
Биологизаторский:
способности полностью определяются только наследственностью
Социологизаторский:
способности полностью определяются социальными условиями индивида
Современный подход:
признает наследственность как условие развития способностей, проявляющееся во врожденных задатках,
но в качестве источника развития способностей рассматривает социокультурный опыт, который передается в процессе обучения.

Математические способности
Математические способности - индивидуально-психические особенности человека, проявляющиеся в уровне развития математических схем мышления.
Характеристики математической одаренности:
Быстрое схватывание математической информации;
Тенденция мыслить сокращенно, свернутыми структурами;
Стремление к своеобразной экономии умственных усилий;
Наличие ярких пространственных представлений;
Пониженная утомляемость при занятиях математикой.

Благодарю за внимание!

Под анализом принято понимать:
форму мышления, исследования и познания, когда изучаемый объект мысленно или практически расчленяется на составные части, каждая из которых изучается отдельно, с тем, чтобы в дальнейшем соединились с помощью синтеза в единое целое, рассматриваемое уже на более высоком уровне;
метод рассуждения, при котором мысль движется от неизвестного к известному;
метод мышления от целого к частям этого целого;
приём мышления, при котором переходят от следствия к его причине;
особую форму процесса мышления, когда объект включается во всё новые связи и в силу этого выступает во все новых качествах, которые фиксируются в новых понятиях.

Синтезом называют:
форму мышления, исследования и познания, когда изучаемый объект мысленно или практически соединяется в единое целое из составных частей объекта, расчленённого в процессе анализа;
метод рассуждения, при котором мысль движется от известного к неизвестному;
метод мышления от частей к целому;
приём мышления, при котором переходят от причины к её следствию;
особую форму процесса мышления, когда происходит соотнесение, сопоставление и установление всяких связей между различными элементами.

Под обобщением понимают мысленное выделение, фиксирование каких-либо свойств, принадлежащих только данному множеству объектов и объединяющих эти объекты воедино.
Специализация есть мысленное выделение некоторого свойства из множества свойств изучаемого объекта.
При сравнении мысленно устанавливаются сходства или различия объектов изучения.
Аналогией называют метод познания, с помощью которого сходство предметов, выявленное в результате их сравнения, распространяется на новое свойство.