Слайд 2Введение
Если две прямые, лежащие в одной плоскости, пересечены третьей и если сумма

внутренних односторонних углов меньше двух прямых углов, то эти прямые пересекутся с той стороны, где это имеет место.
Слайд 8Аксиома
Через точку, лежащую вне прямой в плоскости, определяемой ими, можно провести не

менее двух прямых, не пересекающих данную прямую.
Слайд 10Основная теорема
Пусть в плоскости даны прямая a и не лежащая на ней

точка A. Тогда в пучке прямых с центром в точке A существуют две пограничные прямые, разделяющие все прямые пучка на два класса: на класс прямых, пересекающих a, и класс прямых, не пересекающих a. Эти граничные прямые сами не пересекают a.
Слайд 11Определение
Прямая C'C называется параллельной прямой B'B в направлении B'B в точке A,

если, во-первых, прямая C'C не пересекает прямой BB', во-вторых, C'C является граничной в пучке прямых с центром в точке A, то есть всякий луч AE, проходящий внутри угла CAD, где D – любая точка прямой BB', пересекает луч DB.
Слайд 12Сферическая геометрия
Определение 1 Большим кругом называется часть плоскости, которая проходит через центр

сферы.
Определение 2 Любая плоскость, которая не проходит через центр сферы, называется малым кругом.
Слайд 14Определение сферического треугольника
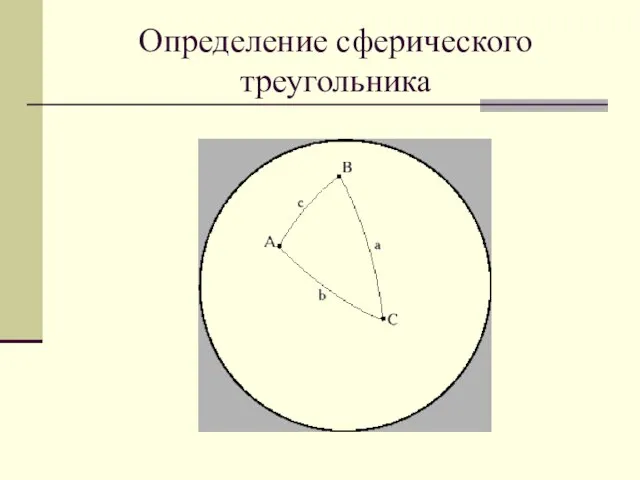
Слайд 15Вычисление площади сферического треугольника
S = R2(A + B + C –
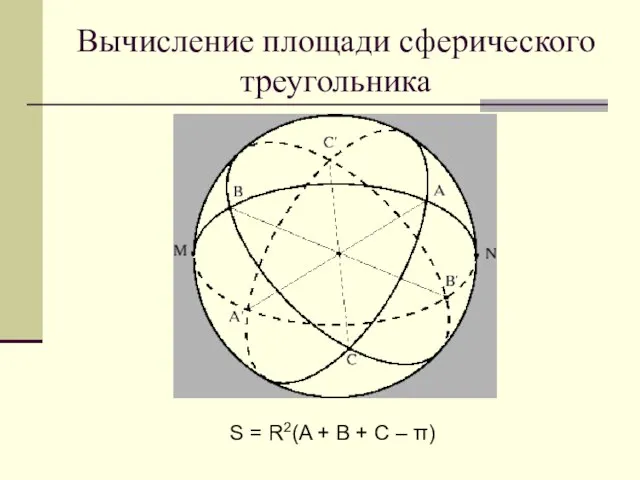
π)













 Евстафьев А.И. Начальник отдела консалтинга ООО “Южная Юридическая Консалтинговая Компания”, САРН Максимов Д.В. Финансовый дире
Евстафьев А.И. Начальник отдела консалтинга ООО “Южная Юридическая Консалтинговая Компания”, САРН Максимов Д.В. Финансовый дире Базовая станция МегаФон
Базовая станция МегаФон Матюшевский Дом культуры приглашение в дни весенних праздников
Матюшевский Дом культуры приглашение в дни весенних праздников Бизнес инсайт. Саша Лонго. Как стать человеком-магнитом
Бизнес инсайт. Саша Лонго. Как стать человеком-магнитом Полевые транзисторы. Самостоятельная работа
Полевые транзисторы. Самостоятельная работа МОНИТОРЫ
МОНИТОРЫ Важнейшие географические открытия. Марко Поло и его путешествия.
Важнейшие географические открытия. Марко Поло и его путешествия. Уголовно - правовые отношения
Уголовно - правовые отношения Создание базы знаний по флоре Байкальской Сибири
Создание базы знаний по флоре Байкальской Сибири Наброски и зарисовки архитектурных строений и их элементов. Пленэр
Наброски и зарисовки архитектурных строений и их элементов. Пленэр Кому нужен ВСД. Комплексная транспортная система Санкт-Петербурга
Кому нужен ВСД. Комплексная транспортная система Санкт-Петербурга Традиции празднования Рождества в США
Традиции празднования Рождества в США Время любви - весна
Время любви - весна Презентация на тему ХАМЕЛЕОНЫ
Презентация на тему ХАМЕЛЕОНЫ  Formy prac florystycznych
Formy prac florystycznych Традиции семьи для квеста
Традиции семьи для квеста Как выполнить чертёж Брусок /стойка/. 10, 11 класс
Как выполнить чертёж Брусок /стойка/. 10, 11 класс Правовые символы
Правовые символы ОАО «РУСДЖАМ КИРИШИ»
ОАО «РУСДЖАМ КИРИШИ» 732 Вот год пришёл к кончине
732 Вот год пришёл к кончине Русская культура в конце XIII- начале XIV веков
Русская культура в конце XIII- начале XIV веков Порядок назначения и выплаты пособий семьям с детьми в РФ
Порядок назначения и выплаты пособий семьям с детьми в РФ КЕЙС. СТРАТЕГИЯ РОСТА
КЕЙС. СТРАТЕГИЯ РОСТА Я буду конструктором, проектировщиком или архитектором – детские мечты в реальность
Я буду конструктором, проектировщиком или архитектором – детские мечты в реальность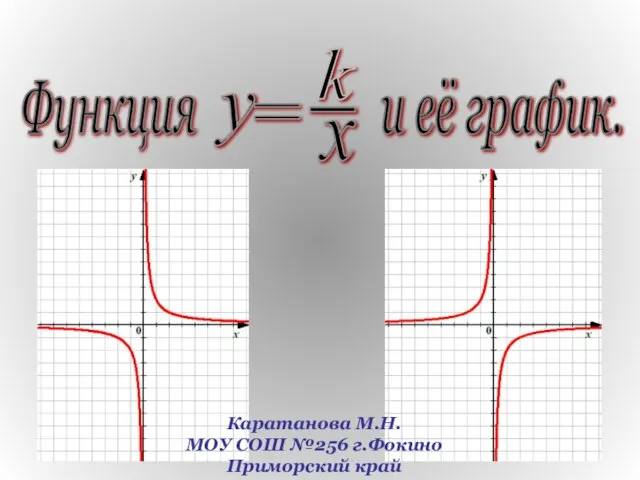 Презентация на тему Функция и её график
Презентация на тему Функция и её график  ЖИВОПИСЬ 14 — 15 ВЕКОВ НА РУСИ
ЖИВОПИСЬ 14 — 15 ВЕКОВ НА РУСИ  #Pokupanda_Tomsk
#Pokupanda_Tomsk FEATURES OF DRUGS ACTION DURING PREGNANCY
FEATURES OF DRUGS ACTION DURING PREGNANCY