Работа в MS Excel

Microsoft Excel – это программа, предназначенная для создания электронных таблиц и управления ими, позволяющая обрабатывать числовые данные, создавать графики и анализировать информацию баз данных

Преимуществом MS Excel является то, что программа помогает оперировать большими объемами информации.
Рабочие книги MS Excel предоставляют возможность хранения и организации данных, вычисление суммы значений в ячейках.
Ms Excel предоставляет широкий спектр методов позволяющих сделать информацию простой для восприятия.

Особенность электронных таблиц заключается в возможности применения формул для описания связи между значениями различных ячеек.
Расчёт по заданным формулам выполняется автоматически. Изменение содержимого какой-либо ячейки приводит к пересчёту значений всех ячеек, которые с ней связаны формульными отношениями и, тем самым, к обновлению всей таблицы в соответствии с изменившимися данными.

Основные возможности электронных таблиц:
Проведение однотипных сложных расчётов над большими наборами данных;
Автоматизация итоговых вычислений;
Обработка (статистический анализ) результатов экспериментов;
Подготовка табличных документов;
Построение диаграмм (в том числе и сводных) по имеющимся данным;
Создание и анализ баз данных (списков).

Запуск программы MS Excel 2003
Необходимо выполнить следующую последовательность действий: Пуск → Все программы →
Microsoft office →
Microsoft office Excel 2003

Основные понятия более новой версии приложения - MS Excel 2007
Лента - состоит из вкладок.
Каждая вкладка относится к определенной категории работ. Первая слева вкладка — вкладка Главная — содержит наиболее часто используемые команды.
Связанные команды на ленте организованы в группы.

Книги и листы
Столбцы, строки и ячейки,
из которых состоят листы
Ячейки — это области, куда вводятся данные

Основные компоненты окна Excel:
Строка заголовка
Строка меню
Панели инструментов
Строка формул
Окно рабочей книги
Строка состояния
Область задач

Строка заголовка
У левого края этой строки указано название программы и имя текущей рабочей книги.
У правого края строки заголовка расположены три кнопки, с помощью которых можно управлять окном программы Excel. (Свернуть, Свернуть в окно или Развернуть во весь экран, Закрыть)

Строка меню
– содержит названия меню программы Excel, обращение к которым открывает доступ ко всем командам и параметрам приложения.
Каждый пункт меню представляет собой набор команд, объединенных общей функциональной направленностью.
Чтобы открыть то или иное меню с перечнем определенных команд, необходимо щелкнуть мышью на его названии. Для того чтобы выбрать команду меню, достаточно щелкнуть на названии этой команды.

Панели инструментов
Кнопки на этих панелях называются инструментами.
Инструменты предназначены для быстрого запуска наиболее распространенных команд и действий Excel.
По умолчанию отображены только две панели инструментов:
Стандартная и Форматирование.

Строка формул
Строка формул, содержащая в качестве элементов поле Имя и кнопку Вставка функции (fx), предназначена для ввода текста, чисел и формул в ячейки таблицы.
Если ввод данных осуществляется непосредственно в ячейки таблицы Excel, то в этой строке отображается вся вводимая информация.
Адрес текущей ячейки отображается в поле Имя, которое расположено слева от строки формул.

Окно рабочей книги
Рабочая область (активный рабочий лист) - делится на строки и столбцы.
Столбцы обозначаются буквами латинского алфавита от A до ZZ, строки – цифрами.
Место пересечения строки и столбца называется ячейкой. Адресом ячейки служат буква и число, соответствующие пересекающимся в ячейке столбцу и строке.
Полосы прокрутки (вертикальная и горизонтальная).
Ярлычки листов для перемещения между рабочими листами.

Структура электронных таблиц
Рабочая книга представляет собой набор рабочих листов, каждый из которых имеет табличную структуру.
В окне документа отображается только текущий (активный) рабочий лист, с которым и ведётся работа.
Каждый рабочий лист имеет название, которое отображается на ярлычке листа в нижней части окна. С помощью ярлычков можно переключаться к другим рабочим листам, входящим в ту же рабочую книгу.

Тренировка навыков работы с листами
Переименование ярлычка листа
Перемещение с одного листа на другой (с помощью сочетания клавиш CTRL+PAGE DOWN и CTRL+PAGE UP)
Назначение цвета ярлычкам листов
Добавление и удаление листов

Рабочий лист (таблица) состоит из строк и столбцов.
Столбцы озаглавлены прописными латинскими буквами и, далее, двухбуквенными комбинациями. Всего рабочий лист содержит 256 столбцов, поименованных от A до IV. Строки последовательно нумеруются числами от 1 до 65536.
На пересечении столбцов и строк образуются ячейки таблицы. Они являются минимальными элементами, предназначенными для хранения данных. Каждая ячейка имеет свой адрес.

Адресация ячеек
Адрес каждой ячейки состоит из символа буквы или букв, обозначающих столбец, и цифры, обозначающей номер строки. Например: А1, В1,С1 и т.д.
Ссылка на целую группу ячеек (Диапазон) обозначается как адрес верхней левой ячейки диапазона, затем двоеточие (:) и адрес нижней правой ячейки этого же диапазона.
Например: =A1:C1

Для того чтобы сделать ссылку на ячейку другого рабочего листа (расположенного в текущей рабочей книге), необходимо ввести имя этого рабочего листа, затем восклицательный знак (!) и адрес нужной ячейки. Например, ссылка на ячейку В2 рабочего листа под именем Лист2 выглядит следующим образом: Лист2!В2

Просмотр заголовков столбцов и использование поля «Имя»
Уже в готовой электронной таблице по необходимости можно добавить, удалить, скрыть одну или несколько ячеек, столбцов, строк.
Также можно изменять ширину столбца (или высоту строк) и перемещаться по листу с помощью поля «Имя».

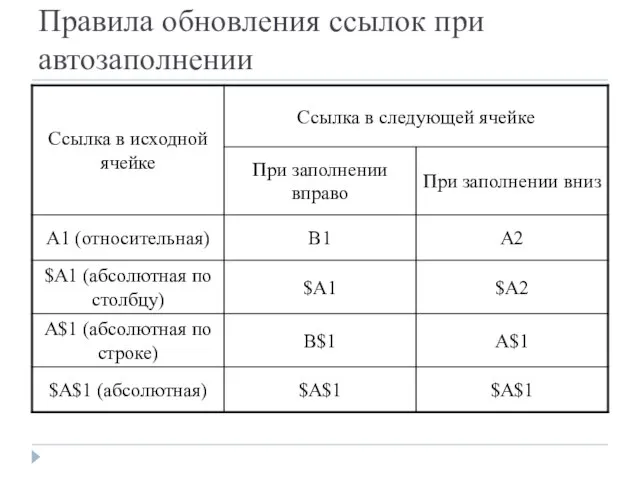
Абсолютный адрес - это не изменяющийся при копировании формулы адрес ячейки, содержащей исходные данные. Для указания абсолютной адресации вводится символ $.
Относительный адрес – это изменяющийся при копировании формулы адрес ячейки, содержащей исходные данные. Такой адрес в своем имени не содержит символ $.

Правила обновления ссылок при автозаполнении

Ввод и сохранение информации
1) Активизировать нужную ячейку
2) Начать вводить информацию
3) Для того чтобы введенные вами данные остались в ячейке, нажмите клавишу
. В случае если вы решили остановить процесс ввода данных, нажмите клавишу
Быстрый ввод данных и создание примечаний
Ввод и редактирование данных

Типы вводимых данных
Числовые данные
Текст
Даты
Время
Формулы
Функции

Примеры ввода данных
В приложении Excel текст выравни-вается по левому краю ячеек, но даты, числа выравниваются по правому краю.
Чтобы ввести текущую дату, нажмите сочетание клавиш CTRL+; (точка с запя-той), текущего времени - CTRL+SHIFT+;.
При вводе дробей оставляйте пробел между целой и дробной частями числа.
“( )” – обозначение отрицательного числа.

Форматирование данных
Вкладки диалогового окна
Формат ячеек:
Число
Выравнивание
Шрифт
Граница
Вид
Защита

ЧИСЛО – позволяет явно определить тип данных в ячейке и форму представления этого типа. Например, для числового или денежного формата можно определить количество знаков после запятой.

ВЫРАВНИВАНИЕ – определяет способ расположения данных относительно границ ячейки. Если включен режим “ПЕРЕНОСИТЬ ПО СЛОВАМ”, то текст в ячейке разбивается на несколько строк. Режим позволяет расположить текст в ячейке вертикально или даже под выбранным углом.

ШРИФТ – определяет параметры шрифта в ячейке (наименование, размер, стиль написания).
ГРАНИЦА – обрамляет выделенные ячейки, при этом можно определить толщину линии, ее цвет и местоположение.

ВИД – закрашивает фон ячеек с помощью выделенного цвета или узора.
ЗАЩИТА – устанавливается защита на внесение изменений.

Практическое задание
Создайте таблицу . При создании таблицы примените следующие установки:
основной текст таблицы выполнен шрифтом Times New Roman 12 размера;
текст отцентрирован относительно границ ячейки;
чтобы текст занимал в ячейке несколько строк, используйте режим Формат – Ячейка – Выравнивание;
выполните обрамление таблицы синим цветом, для этого используйте режим Формат – Ячейка – Граница.

Копирование и перемещение данных Использование Буфера обмена
Буфер обмена – программное средство, предназначенное для хранения ранее скопированных или вырезанных данных.
Здесь используются стандартные команды Копировать (или Вырезать) и Вставить.

Использование Формул
Формулы – это математические выражения, предназначенные для вычислений на основе данных, которые введены в другие ячейки рабочего листа. Формула всегда начинается со знака равенства (=). Результат вычисления формулы отображается в той же ячейке, в которую эта формула введена.

В Excel выполнение арифмети-ческих операторов осуществляется слева направо с учетом приоритета одних операторов над другими.
При этом соблюдается следующий порядок:
1. Все операторы, заключенные в
круглые скобки
2. Возведение в степень - “ ^ ”
3. Умножение и деление
4. Сложение и вычитание
Очередность выполнения операций

Встроенные Функции
Функции – это уже готовые, встроенные в Excel формулы, которым присвоены уникальные имена. Также как и формулы, любая функция должна начинаться со знака равенства.
Каждая функция состоит из трех обязательных элементов:

Знак равенства (=). Признак того, что в данную ячейку введена функция или формула, а не данные какого-либо другого типа.
Имя функции. Характеризует тип выполняемых операций.
Аргументы. Значения, на основе которых выполняются вычисления. Аргументы вводят в круглых скобках сразу после имени функции. Как правило, это адреса ячеек, значения которых используются в вычислениях.

В Excel предусмотрено специальное программное средство – Мастер функций.
В главном меню программы выберите команду Вставка → Функция либо щелкните на кнопке ,которая расположена в строке формул. На экране появится диалоговое окно с перечнем встроенных функций программы Excel.

Для быстрого суммирования значений некоторого столбца или строки используется Автосумма.
Для активизации дополнитель-ных функциональных возможностей средства Автосумма предназначены следующие команды.

1) Среднее. Служит для вычисления среднего арифметического значения.
2) Число. Используется для подсчета только числовых значений в указан-ных вами ячейках.
3) Максимум. Сравнивает все значе-ния в указанном вами диапазоне и отображает наибольшее из них.
4) Минимум. Сравнивает все значения в указанном вами диапазоне и отображает наименьшее из этих значений.

Формирование базы данных
Информация в любой базе данных всегда располагается строго в определенном порядке.
Каждую ячейку рабочего листа можно использовать в качестве отдельного поля, а совокупность данных одной строки - в качестве отдельной записи данных.

В Microsoft Excel в качестве базы данных можно использовать список. Список — это способ представления данных, при котором данные в таблице взаимосвязаны и структура таблицы определяется заранее.
Все действия со списками (базой данных) выполняет команда главного меню ДАННЫЕ.

Рекомендации по созданию списка
Размер и расположение списка
На листе не следует помещать более одного списка. Некоторые функции обработки списков, например фильтры, не позволяют обрабатывать несколько списков одновременно.

Между списком и другими данными листа необходимо оставить по меньшей мере одну пустую строку и один пустой столбец. Это позволяет Microsoft Excel быстрее обнаружить и выделить список при выполнении сортировки, наложении фильтра или вставке вычисляемых автоматически итоговых значений.

В самом списке не должно быть пустых строк и столбцов. Это упрощает идентификацию и выделение списка.
Важные данные не следует помещать у левого или правого края списка; после применения фильтра они могут оказаться скрытыми.

2. Заголовки столбцов
Заголовки столбцов должны находиться в первой строке списка. Они используются Microsoft Excel при составлении отчетов, поиске и организации данных, т.е. заголовки столбцов необходимы для однозначной идентификации каждого поля, а также для сортировки и фильтрации записей.

Шрифт, выравнивание, формат, граница и формат прописных и строчных букв, присвоенные заголовкам столбцов списка, должны отличаться от формата, присвоенного строкам данных.

Для отделения заголовков от расположенных ниже данных следует использовать границы ячеек, а не пустые строки или прерывистые линии.

3. Содержание строк и столбцов
Список должен быть организован так, чтобы во всех строках в одинаковых столбцах находились однотипные данные.
Перед данными в ячейке не следует вводить лишние пробелы, так как они влияют на сортировку.
Не следует помещать пустую строку между заголовками и первой строкой данных.

Ввод данных в БД
Введите в ячейки необходимые значения, как при заполнении обычной электронной таблицы.
Активизируйте электронную форму и введите значения полей в ее текстовые поля.

Команда ДАННЫЕ ФОРМА
Форма — это способ представления данных из таблицы, когда на экране представлено содержимое только одной записи.
С помощью формы можно:
заносить данные в таблицу;
просматривать или корректировать данные;
удалять данные;
отбирать записи по критерию.

Использование форм
Щелкните на любой ячейке в строке с заголовками столбцов
В главном меню программы выберите команду Данные →Форма
Название окна формы совпадает с именем текущего рабочего листа, а названия текстовых полей формы аналогичны названиям заголовков столбцов.

Для создания новой записи введите необходимые значения в текстовые поля электронной формы, используя клавишу TAB для перемещения к следующему полю (для перемещения к предыдущему полю используйте сочетание клавиш SHIFT+TAB) и для того чтобы данные, введенные в поля формы, появились в ячейках рабочего листа, щелкните на кнопке Добавить.

Поиск записей в списке
Для того чтобы быстро найти нужную запись, щелкните на кнопке Критерии.
Введите критерии в форме. Чтобы найти совпадающие с критериями записи, нажмите кнопки Далее или Назад. Чтобы вернуться к правке формы, нажмите кнопку Правка.

В критериях допускаются исполь-зование операторов сравнения:
= равно
> больше
< меньше
>= больше или равно
<= меньше или равно
<> не равно

Кроме операторов сравнения, критерии поиска можно задавать с помощью следующих групповых символов:
? - замещает один символ
* - замещает несколько символов
Сортировка записей и использование средства «Автофильтр»

Практическое задание
В первой строке нового рабочего листа наберите головку таблицы со следующими названиями граф:
номер студента,
фамилия, имя,
специальность,
курс,
домашний адрес,
год рождения.

Через команду Данные – Форма занести информацию о 10 студентах.
Hayчитесь просматривать, записи, корректировать и удалять записи из таблицы.
Отберите записи из списка, которые удовлетворяют следующим критериям:
студенты с определенным годом рождения,
студенты определенного курса.

Графическое представление данных
Диаграммы в Excel создаются на основе данных, уже введенных в таблицу, с помощью мастера диаграмм.
Выбор типа диаграммы.
Подкорректировать область данных и ряды.
Настройка опций диаграммы.
Размещение диаграммы.

Средства статистического анализа данных
Средства, которые включены в пакет анализа данных доступны через команду Анализ данных в меню Сервис.
Если этой команды нет в меню, необходимо загрузить надстройку Пакет анализа.

Для анализа данных с помощью этих инструментов следует указать входные данные и выбрать параметры;
Анализ будет выполнен с помощью подходящей статистической макро-функции, а результат будет помещен в выходной диапазон.

Введение в статистику
Статистика – наука об изучении количественной и качественной сторон массовых явлений в их неразрывной взаимосвязи.
Статистика изучает с количественной стороны качественное содержание массовых общественных явлений. Она исследует количественное выражение закономерностей общественного развития в конкретных условиях места и времени.

Санитарная статистика - прикладная наука, которая изучает вопросы, связанные с медициной, гигиеной и общественным здравоохранением, и включает следующие группы вопросов:
Изучение здоровья населения и его основных групп, воспроизводства, рождаемости и смертности, физического развития, продолжитель-ности жизни, распространенности различных заболеваний и т.д.;

Выявление и изучение связей заболеваемости и смертности населения с различными факторами окружающей среды и разработка, на этой основе, оздоровительных мероприятий;
Сбор и изучение данных о сети лечебно-профилактических и санитарно-эпидемиоло-гических учреждений, их деятельности и кадрах для планирования профилактических и лечебно-оздоровительных мероприятий, развития сети, оценки качества работы учреждений;
Изучение и оценка опыта предупреждения и лечения заболеваний;

Содействие планированию, организации и проведению различных лабораторных исследований. Выявление закономерностей различных явлений в организме, определение связи процессов в организме с факторами внешней среды (социальными, антропогенными, природными и др.);
Установление достоверности получаемых результатов и методов профилактики и лечения.

Основные понятия
Статистическая совокупность – это масса отдельных единиц, объединенных единой качественной основой, но различающихся между собой по ряду признаков.
Например, совокупностью будет население какой-либо страны, которое состоит из отдельных людей, различающихся по полу, возрасту и т.д., но она едина в том отношении, что состоит из жителей данной страны.

Виды совокупности
Совокупность – всякое множество отдельных, отличающихся друг от друга и вместе с тем сходных, в некоторых существенных отношениях объектов (единиц) наблюдения.
Совокупность бывает: общая (генеральная), выборочная.

Статистическое наблюдение – это первая стадия статистического исследования, представляющая собой научно организованный по единой программе учет фактов о явлениях и процессах общественной жизни и сбор полученных на основе этого учета массовых первичных данных.
Объектом статистического наблюдения называется совокупность единиц изучаемого явления, о которых должны быть собраны статистические сведения.

Виды статистического наблюдения
Статистическое наблюдение в зависимости от временных характеристик бывает единовременным и текущим.
По охвату единиц изучаемого объекта наблюдение может быть сплошным, когда обследуют все единицы изучаемой совокупности, и не сплошным.
К не сплошному наблюдению относятся анкетное, монографическое и выборочное (частичное), когда обследуют лишь часть единиц изучаемой совокупности.

Результатом сводки статистических материалов могут быть ряды статистических данных, характеризующих либо изменение объемов совокупностей в динамике, либо распределение единиц совокупностей по тем или иным варьирующим признакам.
В первом случае образуются статистические ряды динамики, анализ которых выявляет закономерности динамики.
Во втором случае образуются ряды распределения, анализ которых имеет задачей выявить характер и закономерности распределения.

Рядом распределения называется упорядоченное распределение единиц совокупности на группы по какому-либо варьирующему признаку.
Ряды распределения единиц совокупности по признакам, имеющим количественное выражение, называются вариационными рядами.
Вариационные ряды по способу построения бывают интервальными и дискретными.

Интервальные вариационные ряды - это такие ряды, где значения вариант даны в виде интервалов.
Дискретные вариационные ряды характеризуются тем, что варианты в них имеют значения целых чисел.
В вариационном ряду различают два элемента: варианты (отдельные значения признака) и частоты (числа, которые показывают, как часто встречаются те или иные варианты в ряду.

Вариация и варьирующие признаки
Вариация признака – различия между числовыми значениями единиц изучаемого признака в исследуемой совокупности (между вариантами).
Варианта - значение признака для той или иной единицы совокупности.
Варьирующими признаками называются такие, которые принимают разное значение (качественное или количественное) у отдельных единиц совокупности.

Статистика основана на теории вероятности.
Статистическая вероятность – отражение частоты события, представляющее собой отношение числа случаев данного события к общему числу ситуаций, в которых оно могло бы произойти.
В медицине достоверно событие при его вероятности 95 % или в долях 0,95.
Вероятность ошибки, соответственно, < 5 %, в долях < 0,05.

Различают следующие события :
Обязательные(Достоверные) ;
Невозможные;
Случайные .
Основой теории статистики является Закон больших чисел – при массовых наблюдениях, когда имеем достаточно большое количество однородных явлений, встречающиеся случайные отклонения взаимно погашаются.

Общие методы исследования определяют:
Проведение сводки и группировки статистичес-кого материала,
вычисление относительных и средних величин,
оценка их достоверности.
Показатели, которыми статистика характеризует совокупности единиц в целом или по группам, называются обобщающими показателями.
Они могут быть абсолютными, относительными и средними величинами.

Абсолютные величины получают непосредственно в результате сводки (суммирования) первичного статистического материала.
Относительные величины получают в результате сравнения двух показателей. Знаменатель отношения, т.е. та величина, с которой сравнивают другую, называется основанием, или базой сравнения.

Если основание принять за единицу, то относительная величина выразится в форме коэффициента, она покажет, во сколько раз сравниваемая величина больше или меньше основания.
Относительная величина может быть выражена в процентах, если основание принято за 100.
Она может быть выражена и в проммиле, если основание принято за 1000.

В зависимости от размерности сравниваемых величин выбирают наиболее удобные формы выражения относительных величин.
Если сравниваемая величина намного превосходит основание, то отношение лучше выражать коэффициентом.
В процентах относительные величины выражают тогда, когда величина сравнения не очень сильно отличается по размерности от основания. Если же она очень мала, то относительную величину выражают в проммиле.

Определение средней
Средней величиной в статистике называется обобщающая характеристика совокупности однотипных явлений по какому-либо количественно варьирующему признаку, которая показывает уровень признака, отнесенный к единице совокупности.

Средняя величина характеризует всю массу единиц совокупности и выражает что-то типичное и общее для данной совокупности, но не характеризует отдельные варианты, составляющие совокупность.
Средняя величина как бы абстрагирована от значений отдельных вариант.

Свойства средней арифметической:
если каждую из вариант совокупности, для которой вычисляется средняя арифметическая, увеличить или уменьшить на одну и ту же величину, то и средняя арифметическая увеличится или уменьшится на столько же;
алгебраическая сумма отклонений отдельных вариант от средней арифметической (т.е. разностей между каждой вариантой и средней арифметической с учетом знака) равняется нулю;
сумма квадратов отклонений от средней арифметической меньше суммы квадратов отклонений от любой другой величины, не равной средней арифметической.

Средняя простая и взвешанная
Техника вычисления средней арифметической определяется характером исходных данных.
Если имеются значения варьирующего признака, полученные из наблюдения, то техника вычисления средней арифметической сводится к суммированию вариант и делению полученной суммы на их число. (формула средней арифметической простой)

В случаях, когда варианты повторяются и это выражено частотами, применяют формулу средней арифметической взвешенной:
Нужно перед суммированием умножить варианту на число единиц, которым это значение варианты присуще. Такое умножение в статистике называют взвешиванием, а число единиц, имеющих одинаковые значения признака, - весами, или частотами. Затем сумма произведений значений вариант на веса делится на сумму весов.

Мода и медиана
Модой в статистике называется величина признака (варианта), которая чаще всего встречается в данной совокупности. В вариационном ряду это будет варианта, имеющая наибольшую частоту.
Медианой в статистике называется варианта, которая находится в середине вариационного ряда. Медиана делит ряд пополам, по обе стороны от нее (вверх и вниз) находится одинаковое количество единиц совокупности.

Первым шагом статистического анализа является построение ряда распределения. По своей конструкции ряд распределения состоит из двух столбцов (граф). В одном столбце располагаются варианты (V), в другом – частоты (P). Частоты указывают, сколько раз встречаются одинаковые значения признака в этом ряду.

Количественные признаки у каждой единицы статистического наблюдения принимают некоторое числовое значение. Эти числовые значения выражаются в виде различных вариант.
Для вычисления частоты встречаю-щихся значений есть функция ЧАСТОТА, которая должна быть завершена комбинацией клавиш Shift+Ctrl+Enter.

Определение статистических показателей
Функция МОДА, где нужно указать лишь один параметр: область, моду которой вы хотите получить.
Функция СЧЁТЕСЛИ, определяет как часто встречается заданное значение в данном ряду. Здесь нужно указать два параметра: количество рядов и значение, для которого производится подсчет.

Для функции МЕДИАНА указывается один параметр – диапазон исследуемых значений. Медиана определяет середину выборки. Медиана не останавливается детально на содержании значений. Здесь больше подходит арифмети-ческая середина, т.к. при вычислении используются сами значения.

Формула вычисления
Среднего арифметического значения

Способы вычисления
Функция СРЗНАЧ, для которой указывается в качестве параметра область, где нужно вычислить среднее арифметическое значение.
=СУММ/СЧЁТ, т.е. суммировав область и разделив на количество
Выбрать среднее в контекстном меню строки состояния

Размах и среднее отклонение
Excel располагает двумя функциями, позволяющими получить крайние значения: максимум определяет большее значение в ряде чисел, и минимум – меньшее.
В качестве параметра в обоих случаях указывается область, которую нужно исследовать.

Если вычесть полученное меньшее значение из большего, в результате получим разницу–размах (Амплитуда).
Разность между конкретной вариан-той и средним арифметическим из этого ряда называется отклонением от среднего

Формула для определения среднего отклонения выглядит следующим образом:
Для вычисления среднего отклонения можно воспользоваться функцией СРОТКЛ, где в качестве параметра следует указать область значений.

Способы определения дисперсии
Дисперсия рассчитывается как сумма квадратов отклонений всех значений от среднеарифметического, деленная на количество значений:

Excel предлагает четыре способа определения дисперсии:
ДИСП и ДИСПА оценивают диспер-сию по выборке
ДИСПР и ДИСПРА вычисляют дис-персию для генеральной совокупности
Дополнение А всегда означает, что в расчете учитываются аргументы, которые содержат значение ЛОЖЬ или ИСТИНА.

Стандартное отклонение (Среднеквадратическое)
– это квадратный корень из дисперсии

Для вычисления стандартного отклонения существует четыре функции:
СТАНДОТКЛОН и СТАНДОТКЛОНА – оцениваются по выборке,
СТАНДОТКЛОНП, СТАНДОТКЛОНПА – вычисляются по генеральной совокупности.
Функции с дополнением А учитывают значения истинности.

Коэффициент вариации
– это процентное отношение средне-квадратического отклонения к сред-нему арифметическому

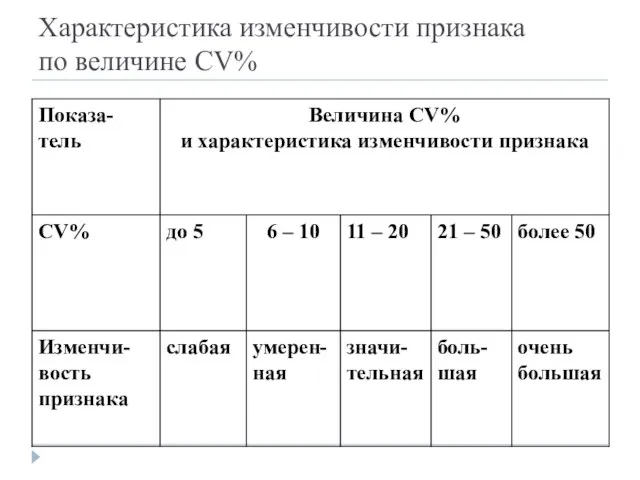
Коэффициент вариации (CV%) –средний процент отклонения вариант от их среднего значения, характеризует те же свойства совокупности, что и среднеквадратическое отклонение.

Характеристика изменчивости признака
по величине CV%

Стандартное отклонение позволяет:
Оценить и охарактеризовать изменчивость вариационного ряда. Чем меньше величина ±σ, тем вариационный ряд компактней, однородней. Чем больше величина ±σ, тем ряд более изменчив, неоднороден.
Определить выскакивающие величины.
Оценить отдельные варианты выборочной совокупности или индивидуум в группе.
Определить достоверность различий между двумя средними величинами

Среднюю ошибку выборки определяют для абсолютной средней арифметической и для относительных средних, характеризующих долю. Определение производят по разным формулам:
Для абсолютных средних:
при числе наблюдений до 30 принимается число степеней свободы (n – 1)

При определении средней ошибки для относительных показателей (доли) используют формулу:
где: p - соответствующая доля; q - все явление, выраженное в долях,(100 - p для случая работы с процентами); n - число наблюдений в выборке.

Закономерности распределения
Существует определенная связь в изменении частот и значения варьирующего признака. Частоты в этих рядах с ростом значения варьирующего признака первоначально увеличиваются, а затем после достижения какой-то максимальной величины в середине ряда уменьшаются. Значит, частоты в этих рядах изменяются закономерно в связи с изменением варьирующего признака и называются закономерностями распределения.

Закономерности распределения выражают какие-то свойства явлений, условия, влияющие на образование вариации.
В статистике часто обращаются к типу кривой нормального распределения потому, что в этом распределении выражается закономерность, возникающая при взаимодействии множества случайных причин.
Кривая нормального распределения симметрична: по обе стороны от ее середины образуются две подобные равномерно убывающие ветви,

асимптотически приближающиеся к оси х. Поэтому в ней средняя арифметическая, мода и медиана совпадают.
В пределах при нормальном распределении заключается 68,3% всех членов распределения.
нормальное распределение далее характеризуется тем, что 95,4% всех членов распределения находятся в пределах, ограниченных точками
а 99,7% всех членов – в пределах, ограниченных точками

t-критерий Стьюдента
отношение разности между сравниваемыми средними величинами к средней ошибке разности.
Каждая из средних величин имеет ошибку.
Соответственно, разность тоже имеет ошибку:

I вариант,
нахождения ошибки для разности
при группах с одинаковым числом наблюдений применяют формулу:

II вариант,
нахождения ошибки для разности
Определение средней ошибки разности для групп с разным числом наблюдений

Формула для нахождения t-критерия Стьюдента
При сравнении групп с равным числом наблюдений используют формулу:

При сравнении групп с разным числом наблюдений используют формулу:

Если вычисленный критерий t больше или равно 2 (t > 2), что соответствует вероятности безошибочного прогноза Р равной или более 95,5% (Р > 95,5% ), то разность следует считать достоверной (существенной), т.е. обусловленной влиянием какого-то фактора, что будет иметь место и в генеральной совокупности.

При t<2 вероятность безошибочного прогноза Р<95,5%.
Это означает, что разность недостоверна, случайна, т.е. не обусловлена какой-то закономерностью (влиянием какого-то фактора).

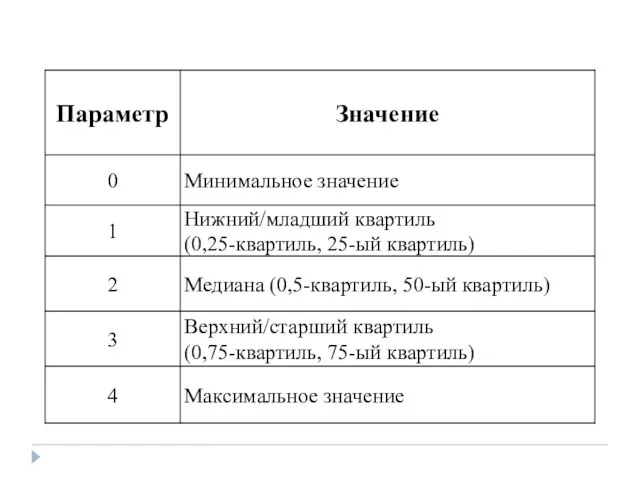
Мера рассеивания – квартиль (четверть)
Так 25-ый квартиль делит пополам отрезок между нижним значением выборки и медианой, 75-ый квартиль – между медианой и верхним значением. Excel содержит функцию:
КВАРТИЛЬ (Массив; Часть)

Под параметром Массив понимается область ячеек числовых значений, для которых должен быть определен квартиль.
Параметр Часть задает, какое значение должно быть получено.
Существуют следующие значения:

Формула вычисления межквартильного размаха выглядит так:
Коэффициент квартильной дисперсии получаем следующим образом:

Практические задания
Создайте таблицу с заголовком “Результаты зачисления”:
Значение последнего столбца может меняться в зависимости от значения набранного бала.

Задача
Создать таблицу для расчета заработной платы: Налог начислить по следующему правилу: если начисление за месяц у сотрудника меньше 100000 тг., то берется 12% от налогооблагаемой суммы. Если начисление больше 100000 тг., то берется 20% от налогооблагаемой суммы.

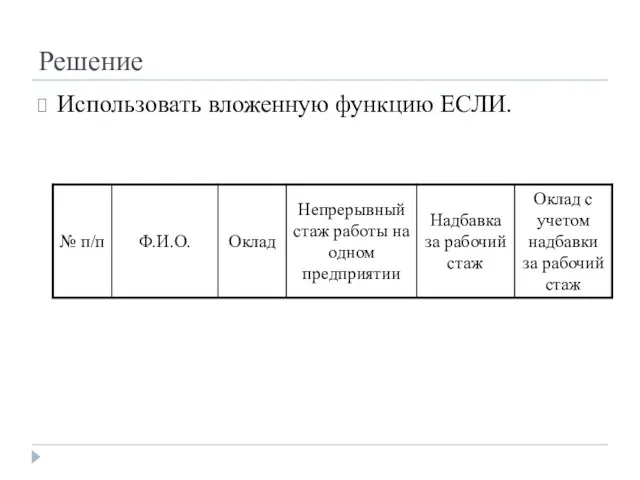
Задача
С целью уменьшения текучести кадров администрация фирмы решила выплачивать надбавку за непрерывный стаж работы на своем предприятии. 10% надбавка к окладу выплачивается работнику, если он проработал на предприятии не менее пяти лет. Если работник проработал на предприятии свыше 10 лет, то надбавка –20%. Провести расчет оклада с учетом надбавки

Решение
Использовать вложенную функцию ЕСЛИ.

Задание 1. Составить таблицу, вычисляющую n-й член и сумму арифметической прогрессии.
Формула n-го члена арифметической прогрессии:
an = a1 + d * (n - 1);
Формула суммы n первых членов арифметической прогрессии: Sn = (a1 + an) * n / 2,
где a1 - первый член прогрессии, а
d - разность арифметической прогрессии.
Перед выполнением упражнения придумайте свою арифметическую прогрессию, т.е. задайте собствен-ный первый член прогрессии и разность.

Ключ к заданию
Введите в ячейку A1 заголовок таблицы. Нажмите Enter. Активизируйте ячейку A1 и выполните команду Формат | Ячейки, на вкладке Выравнивание в разделе Отображение выбрать Переносить по словам.
В ячейку A2 введите d; в ячейку В2 - n; в ячейку C2 - an (для набора нижних индексов воспользуйтесь командой Формат | Ячейки, на вкладке Шрифт активизируйте переключатель Нижний индекс в группе переключателей Видоизменение); в ячейку D2 введите Sn.
В ячейку A3 введите значение разности арифметической прогрессии (d).
В ячейку B3 введите 1, выделите эту ячейку и, удерживая нажатой левую клавишу мыши на маркере заполнения и клавишу Ctrl, заполните диапазон значениями от 1 до 10.
В ячейку C3 введите произвольное значение первого члена арифметической прогрессии.
В ячейку C4 введите формулу: = $C$3 + $A$3 * (B4 - 1). Скопируйте формулу до ячейки C12.
В ячейку D4 введите формулу: = ($C$3 + C3) * B3 / 2. Скопируйте формулу до ячейки D12.

Задание 2. Составить таблицу умножения чисел от 1 до 9.
Ключ к заданию
Введите значения от 1 до 9 в ячейки A2:A10 и B1:J1.
В ячейку B2 введите формулу: = B$1 * $A2.
Используя маркер заполнения, скопируйте формулу сначала вправо, затем, не снимая выделения с полученного блока ячеек, вниз.

Задание 3. Составить таблицу квадратов чисел
от 10 до 99.
Ключ к заданию
Введите значения от 1 до 9 в ячейки A2:A10 и значения от 0 до 9 в ячейки B1:J1.
В ячейку B2 введите формулу: = ($A2 * 10 + B$1)^2.
Используя маркер заполнения, скопируйте формулу сначала вправо, затем, не снимая выделения с полученного блока ячеек, вниз.

Задание 4.
Составить таблицу значений линейной функции
y = kx + b,
выбрав по своему усмотрению свободный член b и угловой коэффициент k.

Ключ к заданию
Объединить ячейки с A1 по N1 и ввести заголовок. Выбрать полужирное начертание шрифта (активизировать ячейку A1 и нажать комбинацию клавиш Ctrl + B).
В ячейки A2 и A3 ввести соответственно x и y, применить выравнивание по центру.
В ячейку В2 ввести значение левой границы выбранного интервала -6, в ячейку С2 ввести следующее число -5. Выделить обе ячейки и протянуть маркер выделения до правой границы интервала.
В ячейку В3 ввести формулу =k*B2+b. Нажать клавишу Enter. Установить курсор на ячейку В3 (она станет активной) и, используя маркер выделения, скопировать формулу для остальных значений x.
Выделить таблицу с заголовком и нажать кнопку Границы

Посчитать сколько прошло дней с даты указанной в ячейке А1 по сегодняшний.
13.04.1923
Посчитать сколько прошло дней с 1/01/1900 до даты указанной в ячейке А1

Написать формулу, которая бы работала следующим образом:
если ячейка A3<0, тогда она должна возврашать 1;
если же 0<=A3<5, тогда должна возвращать 2 + A3;
если же 5<=A3<10, тогда должна возвращать A3-10;
иначе должна возвращать A3 - 20

Подвести итоги и красиво оформить следующую таблицу, используя объединение ячеек, изменение размеров шрифта, эффекты шрифта (полужирный, курсив, подчеркивание, изменение направления текста), создание границ, изменение цвета заливки и цвета шрифта
Построить точно такую же таблицу в процентах. Взять за 100% для любого квартала число всех проданных принтеров за этот квартал