Распространение волн в нелинейной среде

Нелинейная оптика
Лекция 9
Распространение волн в нелинейной среде
Вспомнив, что
исходное волновое уравнение
запишется в виде системы уравнений
Замечания:
В общем виде, нелинейная поляризация определяется всеми полями
Это означает, что перед нами система связанных уравнений
Связанность уравнений означает перераспределение энергии между различными компонентами поля
Частоты справа и слева 0динаковые, а волновые вектора могут быть разными (закон сохранения энергии в стационарном случае и возможность нарушения закона сохранения импульса)

Нелинейная оптика
Лекция 9
Связанные волны в нелинейной среде
Рассмотрим пример трехволнового процесса сложения частоты
Участвуют три волны,
Ограничиваясь дипольным приближением, рассматриваем только
компоненты квадратичной поляризации вида
а компоненты квадратичной восприимчивости подчиняются
следующим перестановочным соотношениям:

Нелинейная оптика
Лекция 9
Связанные волны в нелинейной среде
Система связанных уравнений для трехволнового процесса примет вид:

Нелинейная оптика
Лекция 9
Энергия поля в нелинейной среде
Из уравнений Максвелла можно получить, что
скорость истечения энергии из единицы объема равна скорости убыли
плотности запасенной в нем электромагнитной энергии
Записав полную поляризацию среды в виде
можно ввести мгновенную плотность энергии электромагнитной волны в нелинейной среде:

Нелинейная оптика
Лекция 9
Энергия поля в нелинейной среде
Тогда соотношение
можно записать в виде
Усредненное по времени выражение будет выражать закон сохранения энергии в нелинейной среде:

Нелинейная оптика
Лекция 9
Приближение медленно меняющихся амплитуд
Приближения, упрощающие жизнь:
приближение бесконечных плоских волн
приближение заданной интенсивности накачки
приближение заданного поля
приближение медленно меняющихся амплитуд
Рассмотрим электромагнитную волну в нелинейной среде в виде
для простоты – распространяющуюся вдоль оси z
Амплитуда волны – функция, зависящая от координаты из-за нелинейного взаимодействия
Предположим, что зависимость амплитуды от координаты слабая:

Нелинейная оптика
Лекция 9
Приближение медленно меняющихся амплитуд
Разделив поле на продольную и поперечную компоненты,
волновое уравнение запишется в виде двух уравнений:
тогда, используя:
получим:

Приближение медленно меняющихся амплитуд
Физический смысл приближения – пренебрежение обратной волной
нелинейного сигнала.
Действительно, рассмотрим волновое уравнение в изотропной пластине
Нелинейная оптика
Лекция 9
Будем решать методом функций Грина. ФГ определяется как решение
уравнения
ФГ для однородной пластины принимает вид

Приближение медленно меняющихся амплитуд
Решение волнового уравнения ищем в виде
Нелинейная оптика
Лекция 9
Подставляя выражение для ФГ:
Записав поле внутри пластины как суперпозицию двух разбегающихся волн
и граничные условия на гранях пластины в виде
(постоянство амплитуд вне нелинейной пластины)

Приближение медленно меняющихся амплитуд
получаем:
Нелинейная оптика
Лекция 9
Окончательно:
Но это есть решения двух дифференциальных уравнений
что соответствует уравнениям ММА с

Генерация суммарной частоты в полубесконечной среде
Нелинейная оптика
Лекция 9
В задаче о генерации суммарной частоты участвуют три связанные волны,
каждая из которых раскладывается на две компоненты,
удовлетворяющим волновому уравнению
где

Генерация суммарной частоты в полубесконечной среде
Нелинейная оптика
Лекция 9
В приближении:
бесконечных плоских волн
заданной интенсивности накачки
полубесконечности среды с плоской границей
кубичности (изотропности) среды
уравнения для линейны.
Записав волны накачки в виде
а квадратичную поляризацию в виде
третье связанное уравнение будет иметь решение в виде
и состоит из двух волн, связанной и свободной, с волновыми векторами

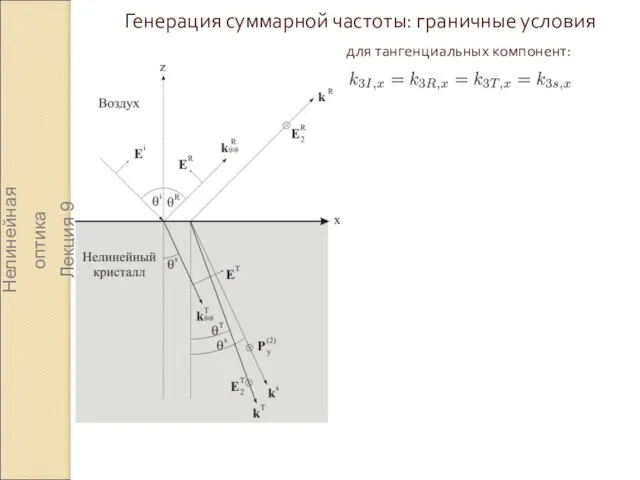
Генерация суммарной частоты: граничные условия
Нелинейная оптика
Лекция 9
для тангенциальных компонент:

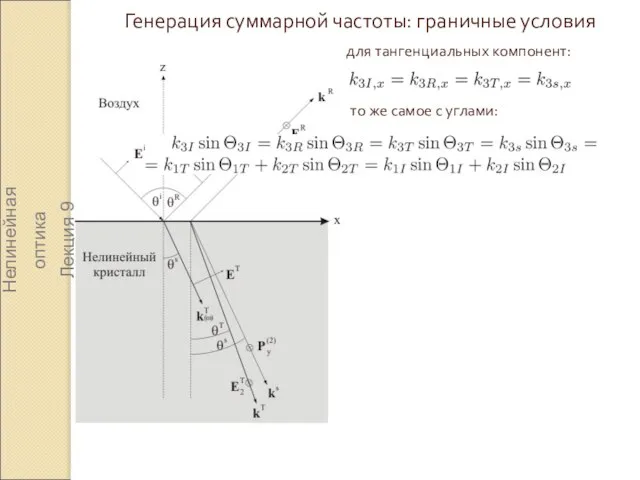
Генерация суммарной частоты: граничные условия
Нелинейная оптика
Лекция 9
для тангенциальных компонент:
то же самое с углами:

Генерация суммарной частоты: фазовый синхронизм
Нелинейная оптика
Лекция 9
Запишем поле на суммарной частоте в виде
тогда в рамках приближения ММА
где расстройка волновых векторов
Решение укороченных уравнений запишется в виде