Содержание
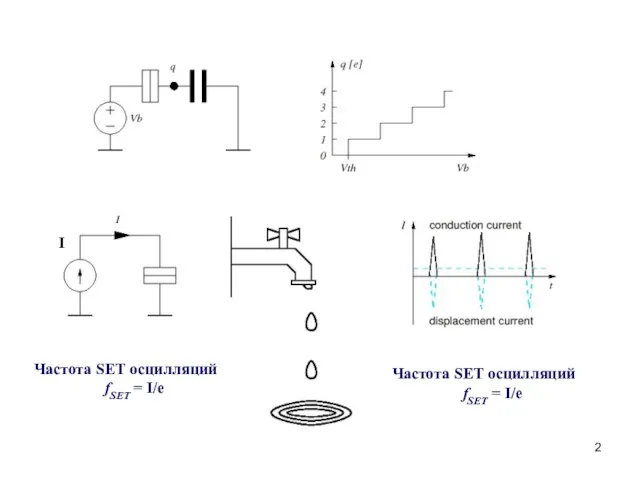
- 2. Частота SET осцилляций fSET = I/e Частота SET осцилляций fSET = I/e I
- 3. Когда же будет достигнут предел миниатюризации обычной электроники? Уже сейчас микроэлектронной промышленностью в опытном порядке создаются
- 4. Выступая в 1975 г. на конференции International Electron Devices Meeting, Гордон Мур отметил, что за прошедшее
- 5. Логические элементы, срабатывающие на определенную величину зарядового пакета, как, например, в случае КМОП-схем, будут слишком часто
- 6. Дальнейшее увеличение тока, обусловленное переходом с низким темпом туннелирования, будет медленным до тех пор, пока на
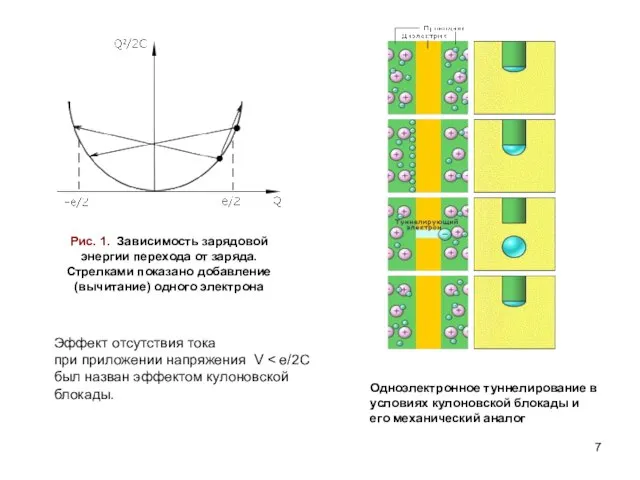
- 7. Эффект отсутствия тока при приложении напряжения V Одноэлектронное туннелирование в условиях кулоновской блокады и его механический
- 8. Figure 1.1: The left side shows, that the electron cloud shift against the lattice of atoms
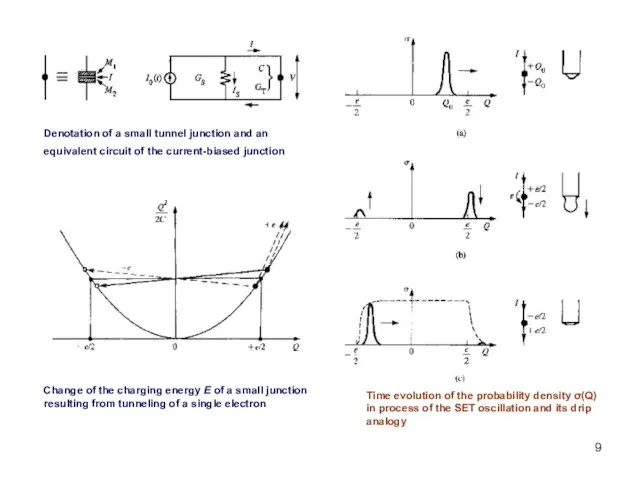
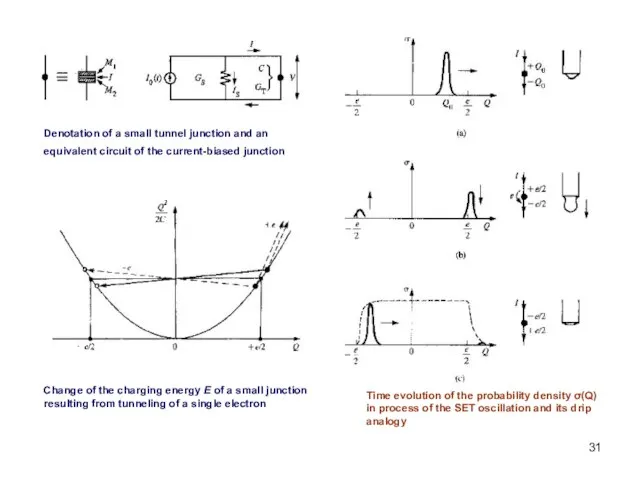
- 9. Denotation of a small tunnel junction and an equivalent circuit of the current-biased junction Change of
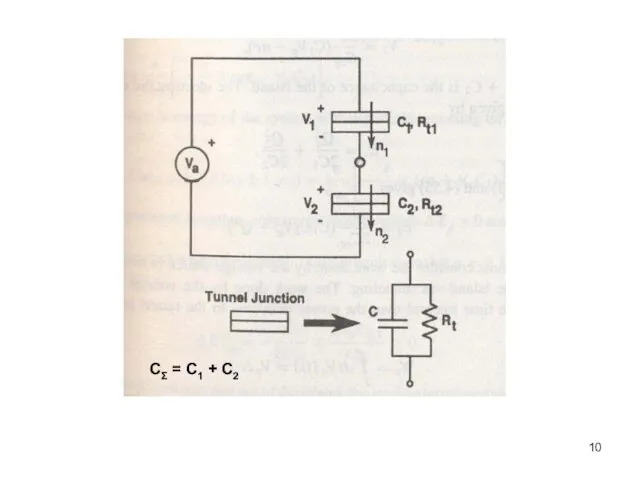
- 10. CΣ = C1 + C2
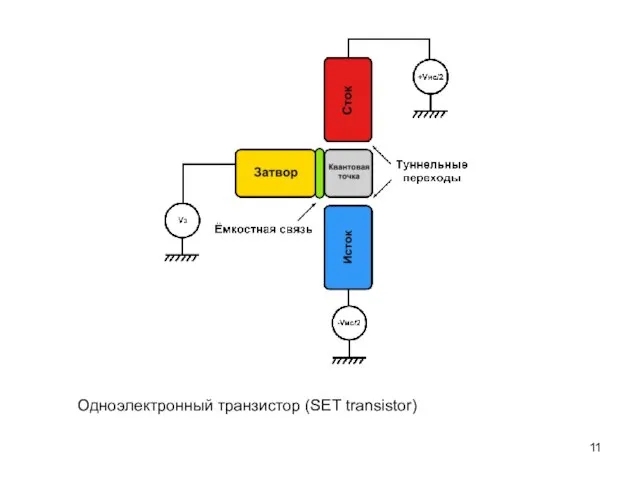
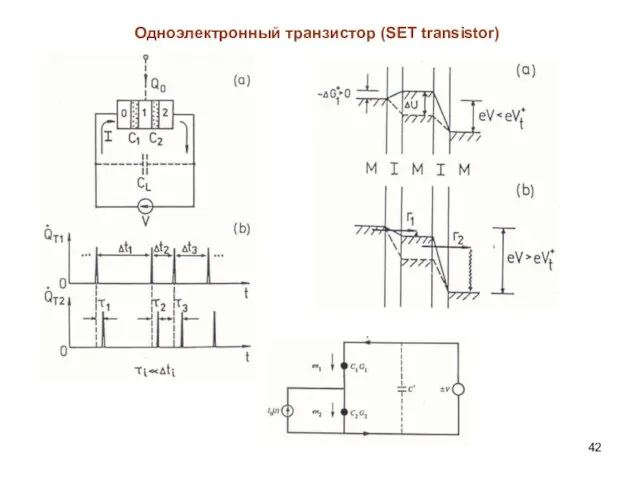
- 11. Одноэлектронный транзистор (SET transistor)
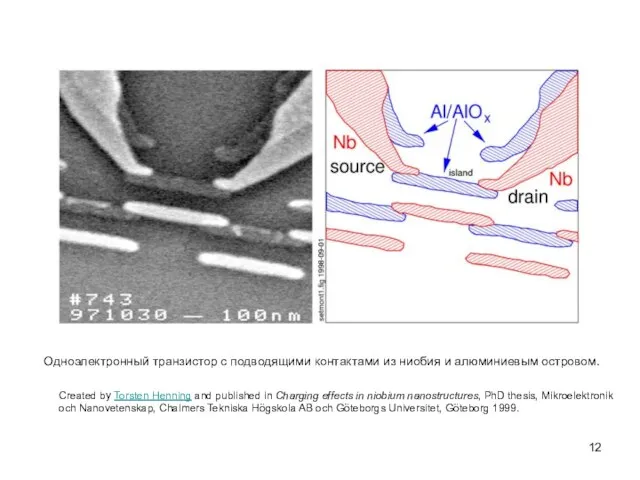
- 12. Одноэлектронный транзистор с подводящими контактами из ниобия и алюминиевым островом. Created by Torsten Henning and published
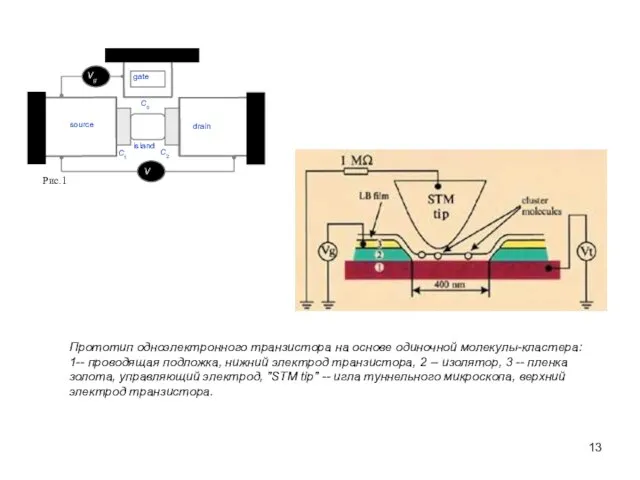
- 13. Прототип одноэлектронного транзистора на основе одиночной молекулы-кластера: 1-- проводящая подложка, нижний электрод транзистора, 2 -- изолятор,
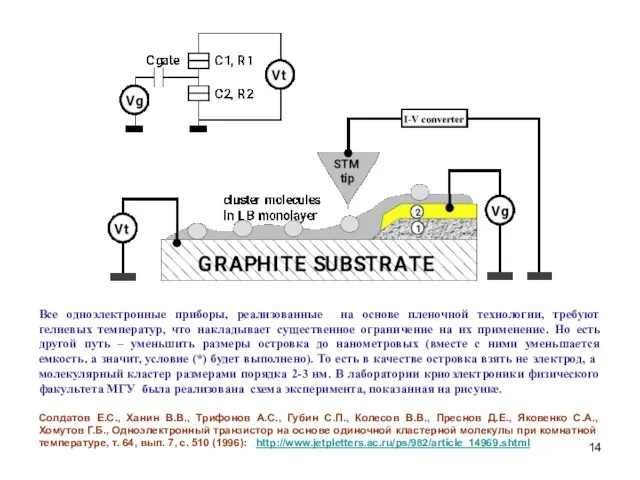
- 14. Все одноэлектронные приборы, реализованные на основе пленочной технологии, требуют гелиевых температур, что накладывает существенное ограничение на
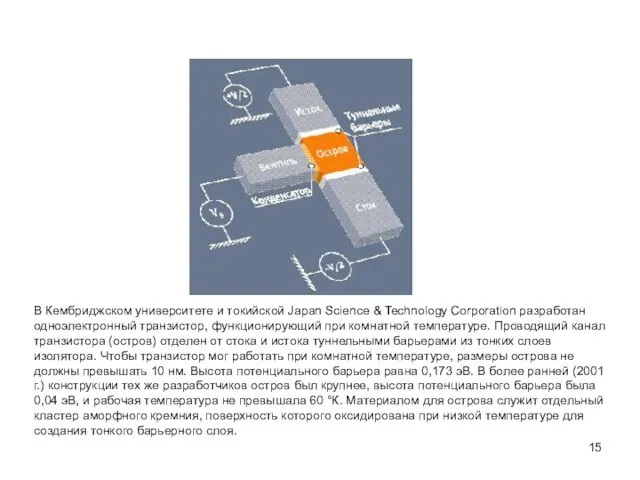
- 15. В Кембриджском университете и токийской Japan Science & Technology Corporation разработан одноэлектронный транзистор, функционирующий при комнатной
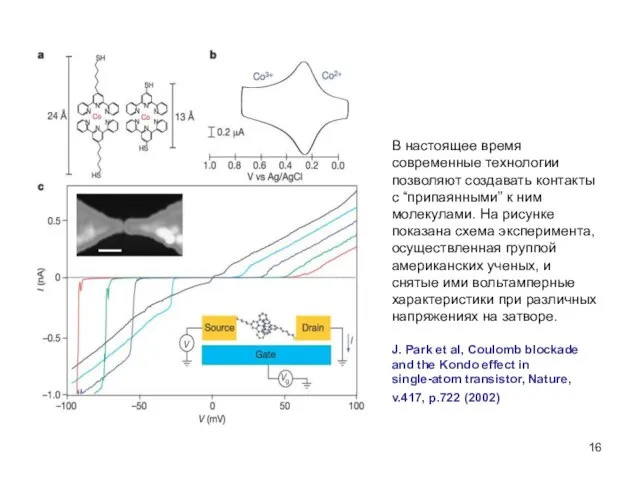
- 16. В настоящее время современные технологии позволяют создавать контакты с “припаянными” к ним молекулами. На рисунке показана
- 17. Ортодоксальная теория. 0-D модель В используемой модели пренебрегается 1) размером и формой туннельного перехода, 2) конечным
- 18. Выражение для туннельного тока (случай большой емкости) Коммутационные соотношения: Электрический ток
- 19. Зная оператор тока, можно вычислить среднее значение тока по формуле Кубо как поправку к равновесному значению,
- 20. Усредняем по большому ансамблю Гиббса: При этом были использованы следующие соотношения:
- 21. Итак, С учетом суммирования по спину:
- 22. Плотность состояний Уравнение Шредингера для свободной частицы В случае ограниченного объема в виде куба со стороной
- 23. Поэтому в сфере объемом число точек, описывающих разрешенные состояния, равно числу ячеек объемом , и поэтому
- 24. Введем обозначение для среднего значения матричного элемента: Выражение для тока: Можно показать, что интеграл в этом
- 25. (закон Ома (!) ) Закон Ома указывает на диссипацию энергии при протекании туннельного тока (!) С
- 26. Учет изменения электростатической энергии при туннелировании Закон сохранения энергии при туннелировании электрона: .
- 27. Рассмотрим систему (х – совокупность ее координат), являющуюся частью замкнутой системы (q – совокупность остальных координат
- 28. Если предположить, что рассматриваемая подсистема находится в некотором полно описанном состоянии с волновой функцией ψ (это
- 29. Если внешний ток I0(t), туннельный ток I и ток через шунт достаточно малы и не нарушают
- 30. Для плотности вероятности можно получить уравнение, используя уравнение Фоккера-Планка для процесса х(t), заданного обыкновенным дифференциальным уравнением,
- 31. Denotation of a small tunnel junction and an equivalent circuit of the current-biased junction Change of
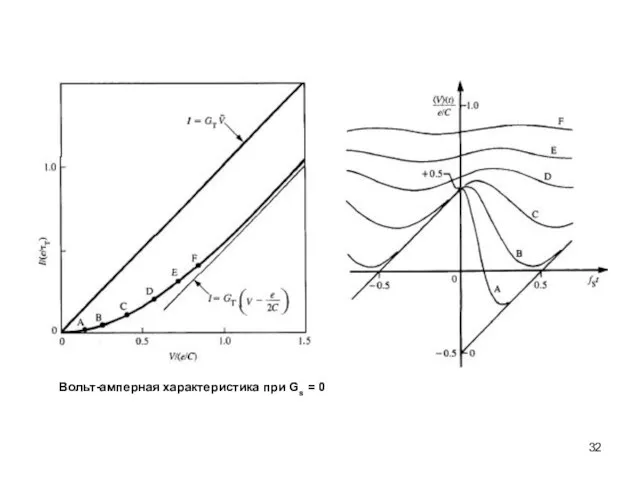
- 32. Вольт-амперная характеристика при Gs = 0
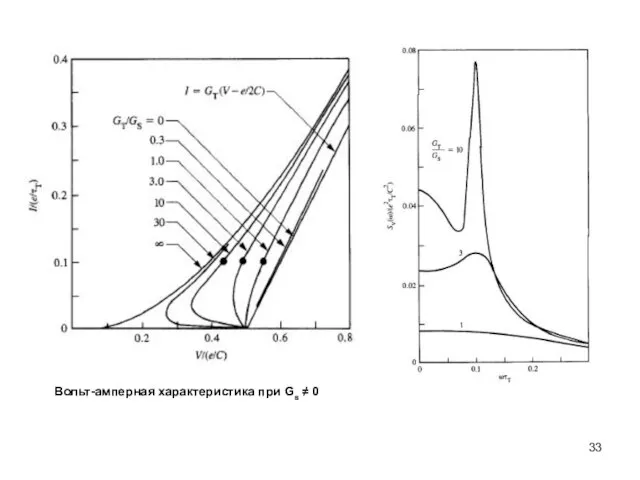
- 33. Вольт-амперная характеристика при Gs ≠ 0
- 34. SIS туннельный переход. Туннелирование куперовских пар Энергетический спектр состоит из зон (полос): n = 0, 1,
- 35. Рассмотрим случай малых флуктуаций: В этом случае система находится внутри нижней зоны (n=0), кроме того, при
- 36. Это будет как раз хорошо известное уравнение Матье (!). Свойства спектра энергии: периодическая зависимость внутри каждой
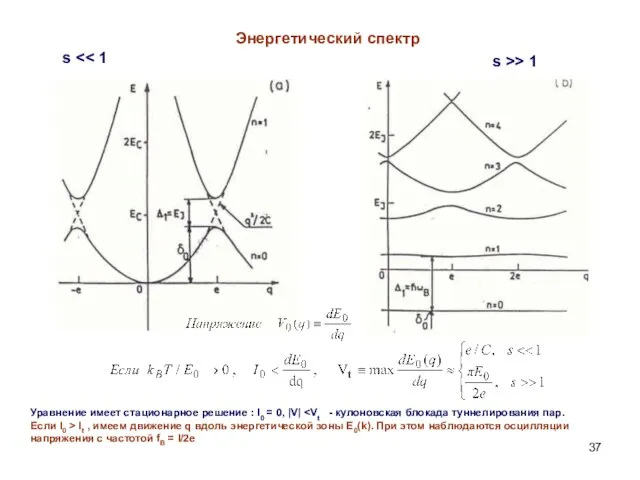
- 37. Энергетический спектр s s >> 1 Уравнение имеет стационарное решение : I0 = 0, |V| Если
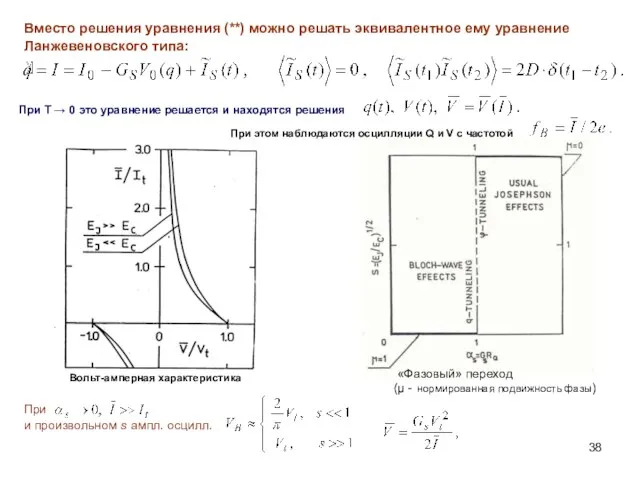
- 38. Вместо решения уравнения (**) можно решать эквивалентное ему уравнение Ланжевеновского типа: При Т → 0 это
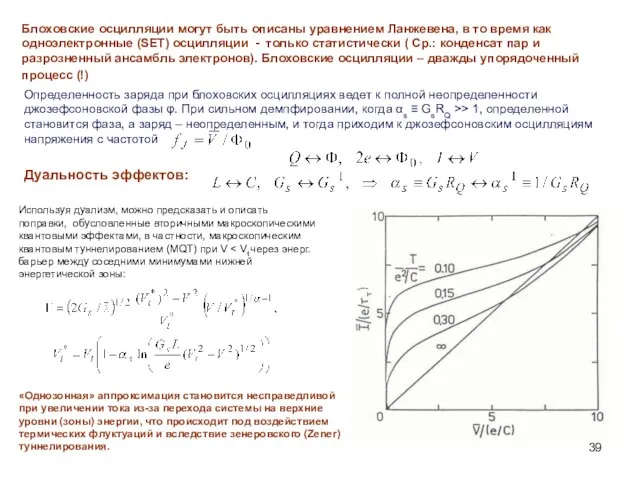
- 39. Блоховские осцилляции могут быть описаны уравнением Ланжевена, в то время как одноэлектронные (SET) осцилляции - только
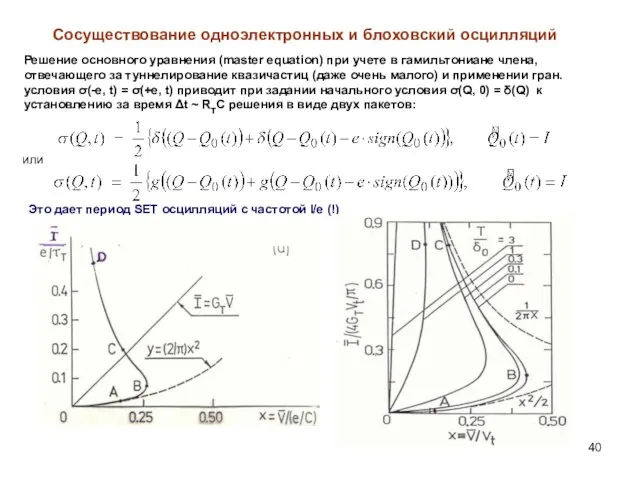
- 40. Сосуществование одноэлектронных и блоховский осцилляций Решение основного уравнения (master equation) при учете в гамильтониане члена, отвечающего
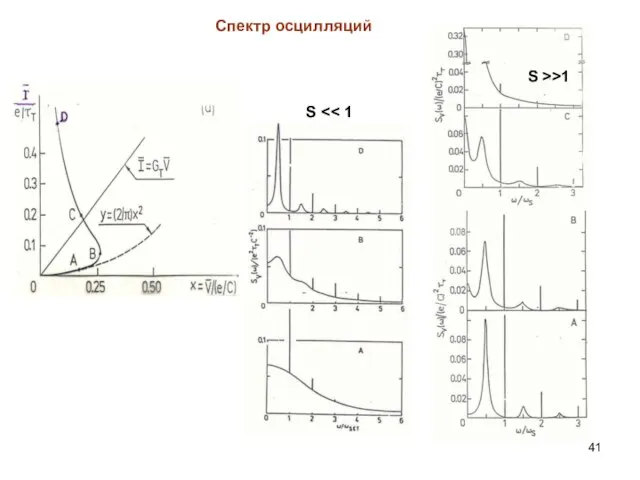
- 41. Спектр осцилляций S S >>1
- 42. Одноэлектронный транзистор (SET transistor)
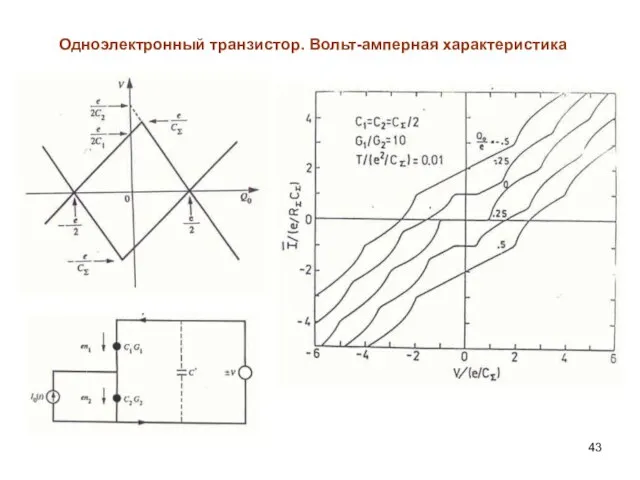
- 43. Одноэлектронный транзистор. Вольт-амперная характеристика
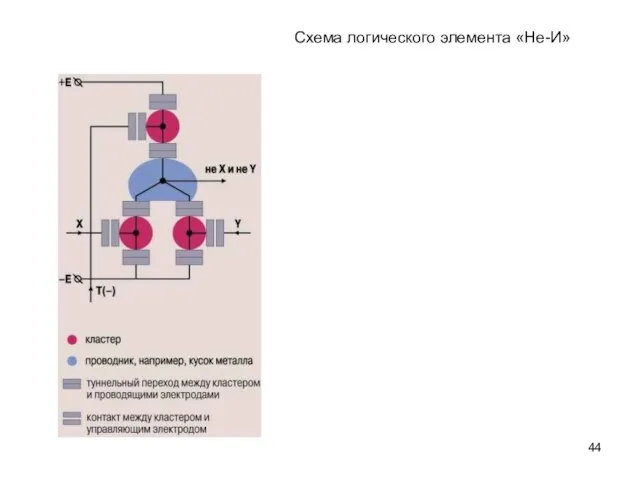
- 44. Схема логического элемента «Не-И»
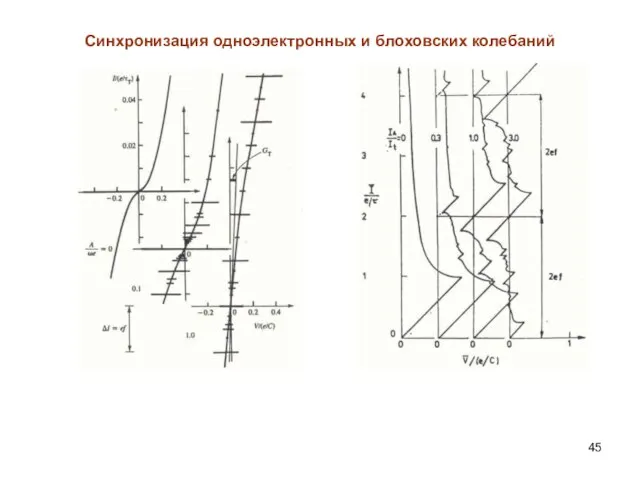
- 45. Синхронизация одноэлектронных и блоховских колебаний
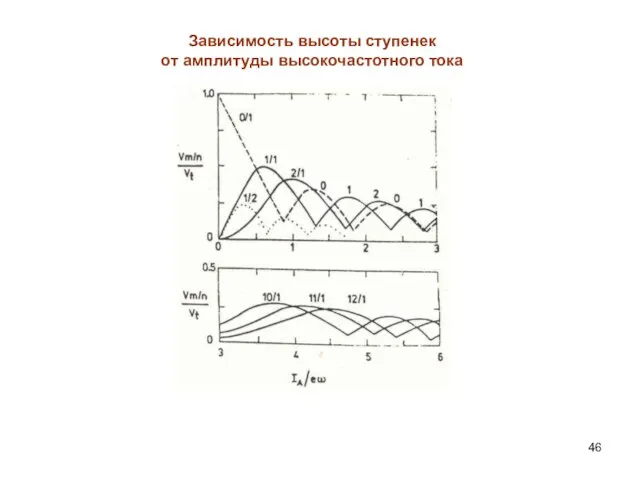
- 46. Зависимость высоты ступенек от амплитуды высокочастотного тока
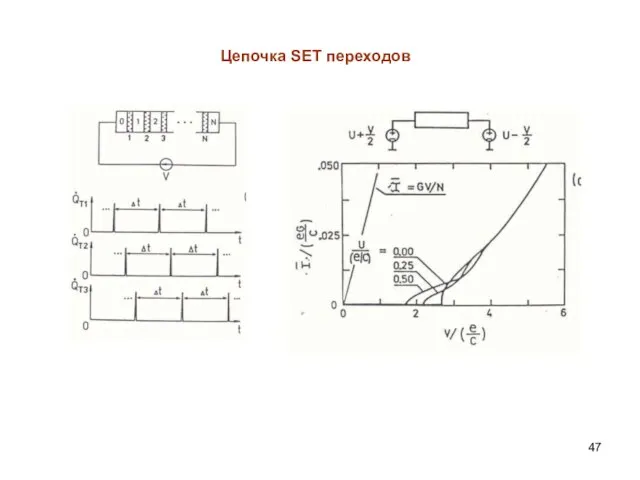
- 47. Цепочка SET переходов
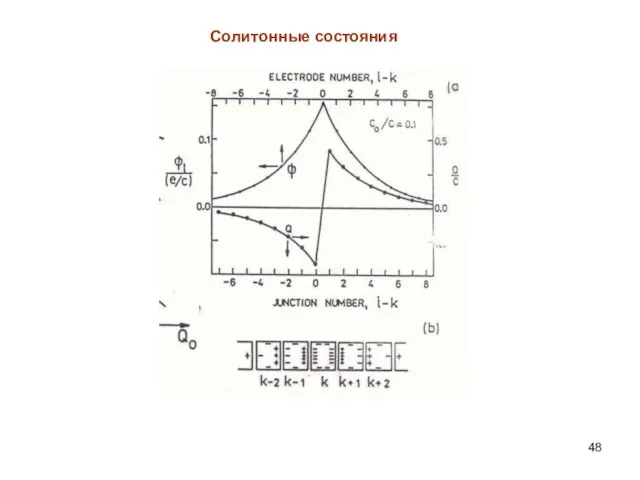
- 48. Солитонные состояния
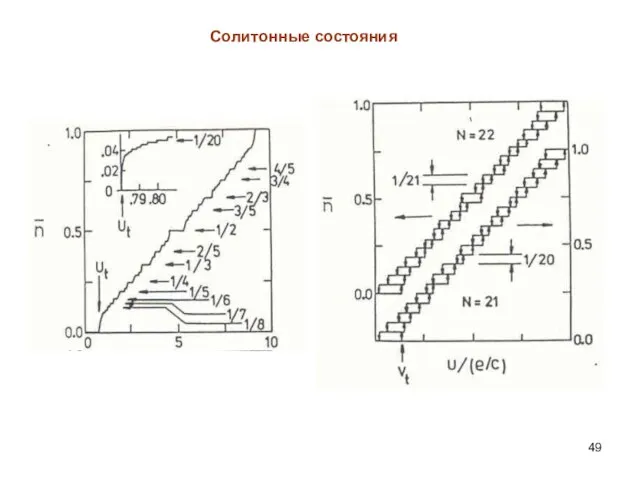
- 49. Солитонные состояния
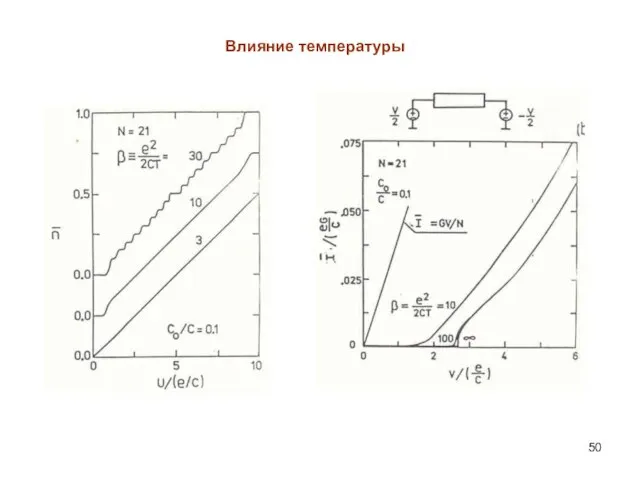
- 50. Влияние температуры
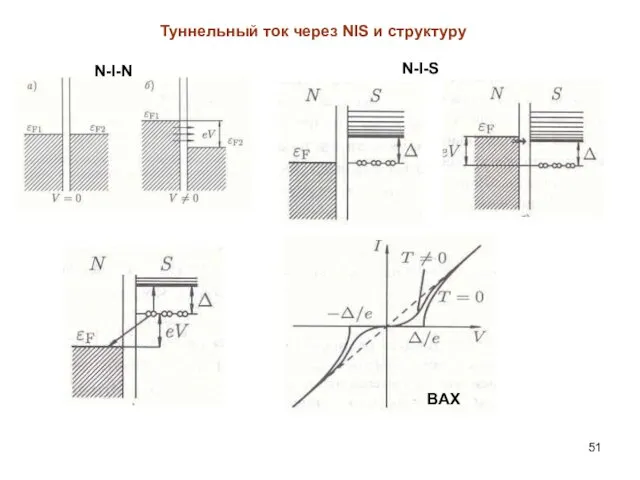
- 51. Туннельный ток через NIS и структуру N-I-N N-I-S BAX
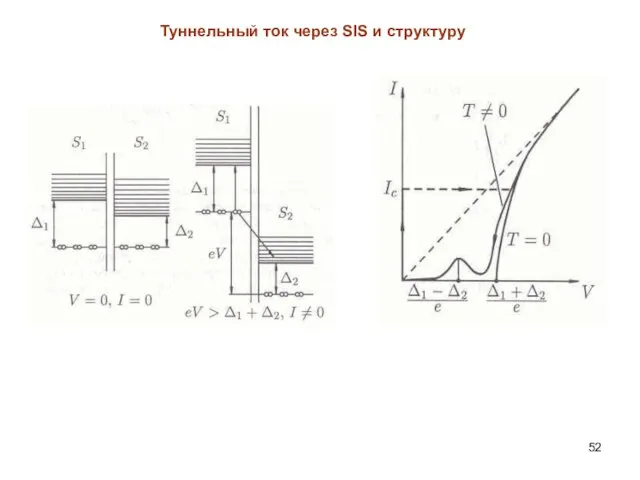
- 52. Туннельный ток через SIS и структуру
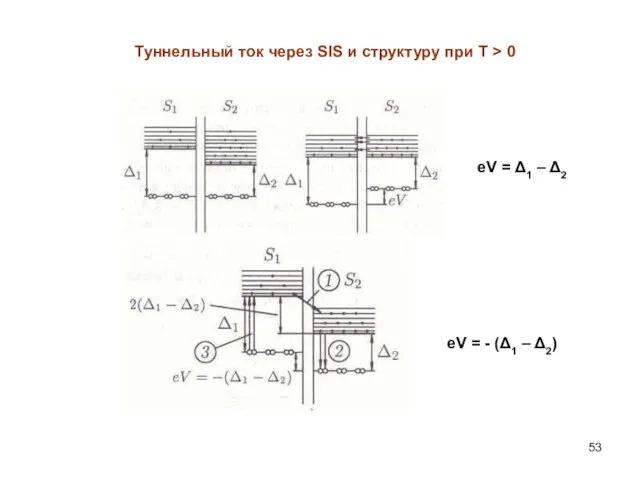
- 53. Туннельный ток через SIS и структуру при Т > 0 eV = Δ1 – Δ2 eV
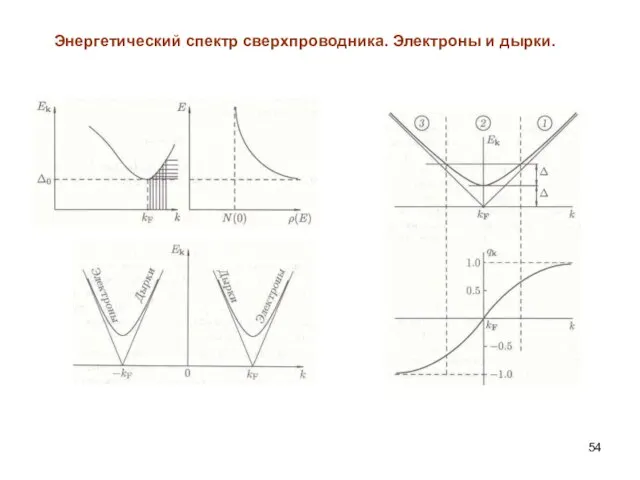
- 54. Энергетический спектр сверхпроводника. Электроны и дырки.
- 55. Андреевское отражение на NS границе
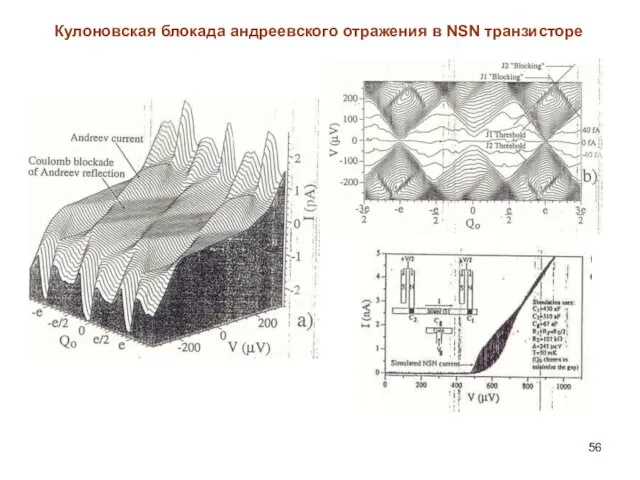
- 56. Кулоновская блокада андреевского отражения в NSN транзисторе
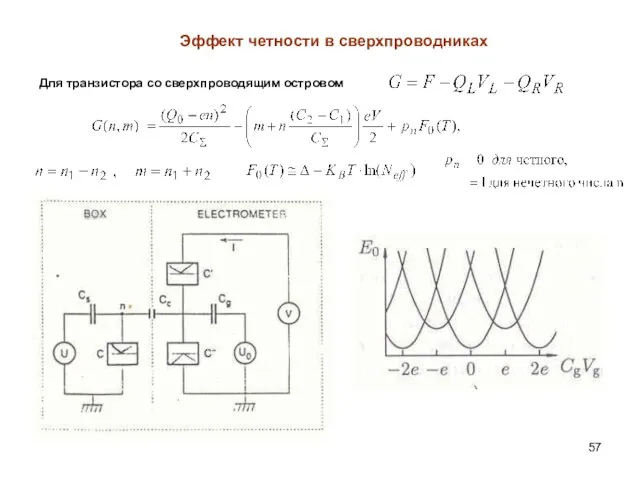
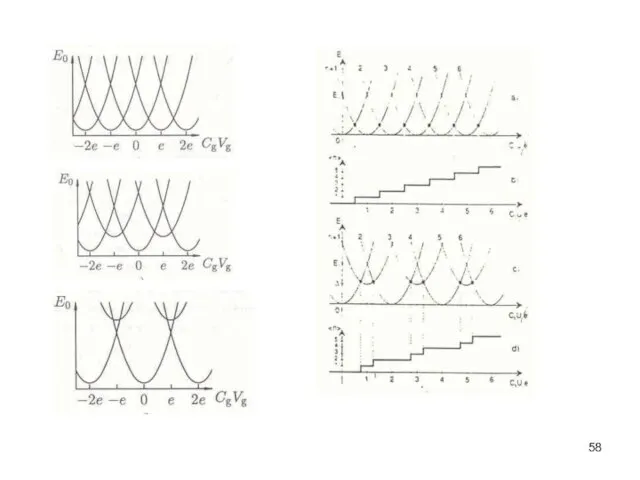
- 57. Эффект четности в сверхпроводниках Для транзистора со сверхпроводящим островом
- 59. Классические вычисления классические алгоритмы; классические биты («0» и «1») «Закон» Мура (элементы микросхем уменьшаются вдвое каждые
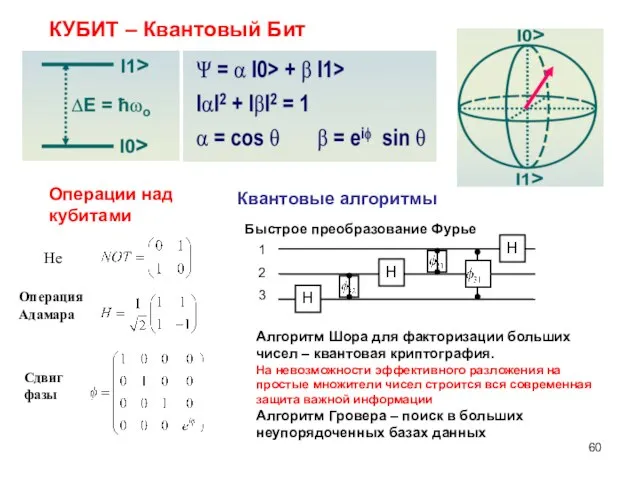
- 60. КУБИТ – Квантовый Бит Операции над кубитами Квантовые алгоритмы Не Операция Адамара Сдвиг фазы Быстрое преобразование
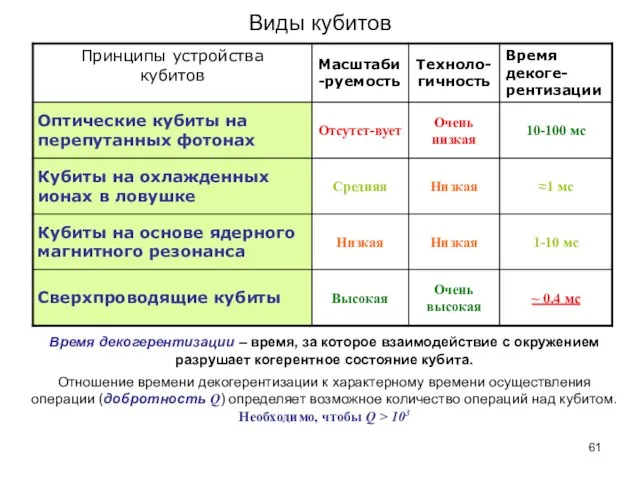
- 61. Виды кубитов Время декогерентизации – время, за которое взаимодействие с окружением разрушает когерентное состояние кубита. Отношение
- 62. Types of Josephson qubits EJ/EQ
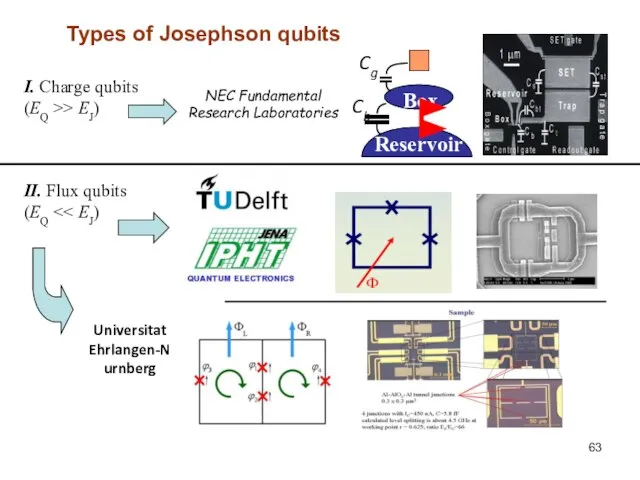
- 63. Types of Josephson qubits I. Charge qubits (EQ >> EJ) NEC Fundamental Research Laboratories II. Flux
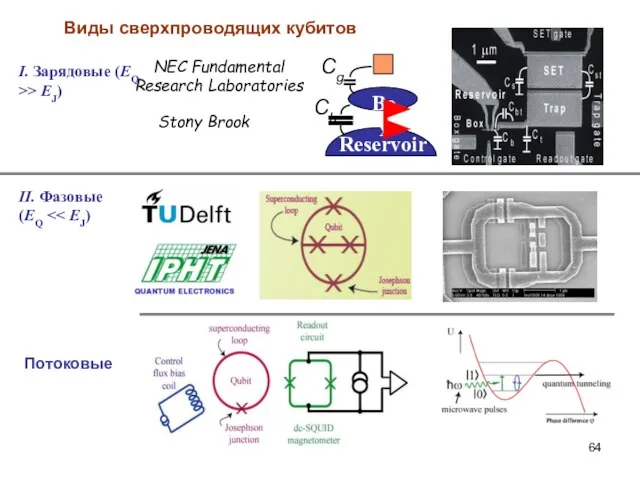
- 64. Виды сверхпроводящих кубитов I. Зарядовые (EQ >> EJ) NEC Fundamental Research Laboratories II. Фазовые (EQ Потоковые
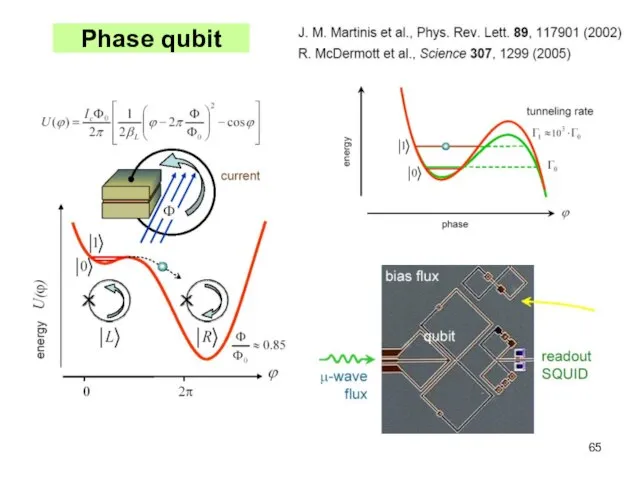
- 65. Phase qubit
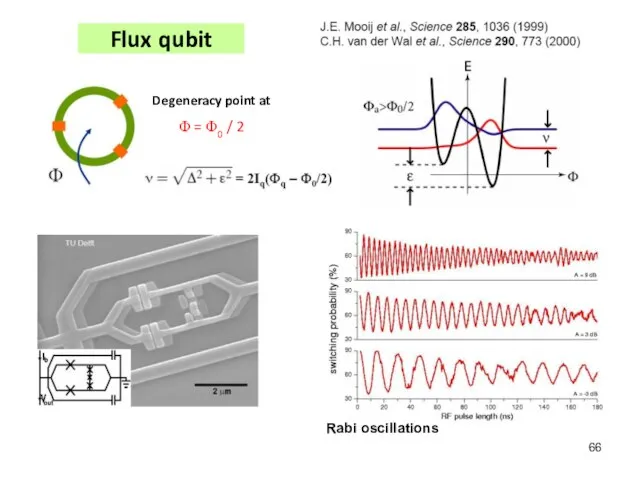
- 66. Flux qubit Degeneracy point at Φ = Φ0 / 2 Rabi oscillations
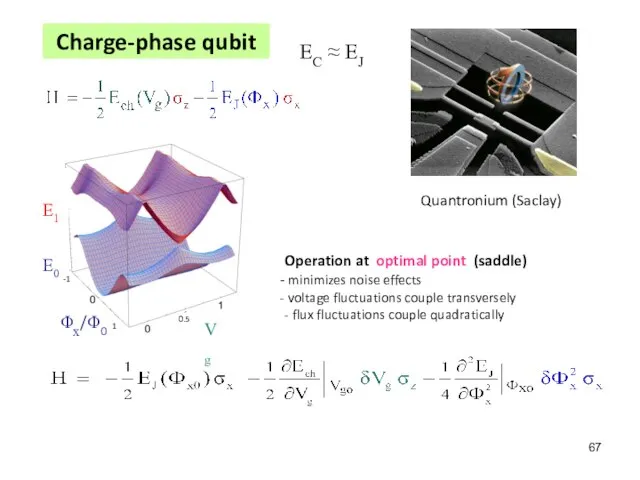
- 67. Quantronium (Saclay) Operation at optimal point (saddle) minimizes noise effects voltage fluctuations couple transversely - flux
- 68. Основные принципы выполнения логических операций Общий вид возмущённого гамильтониана в базисе невозмущённых собственных функций:
- 69. Гамильтонианы кубитов на основе 2-ч- и 3-х-контактных интерферометров. Гамильтониан двухконтактного кубита: Гамильтониан трёхконтактного кубита: Общий метод
- 70. Уравнение для матрицы плотности (уравнение Линдблада) Запутанность (энтропия фон Неймана) Декогеренция – процесс увеличения запутанности с
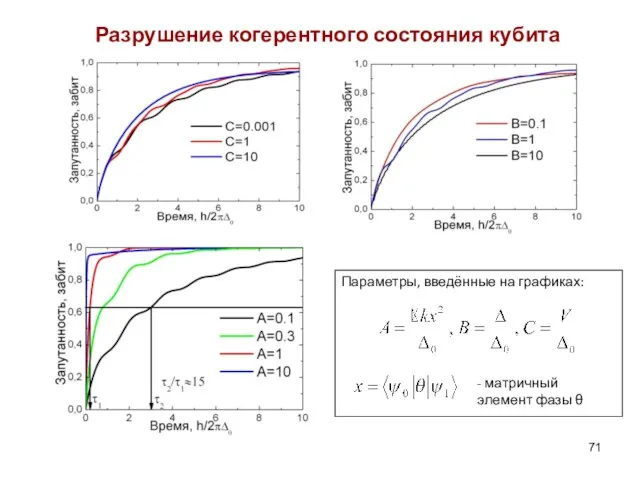
- 71. Разрушение когерентного состояния кубита Параметры, введённые на графиках: - матричный элемент фазы θ
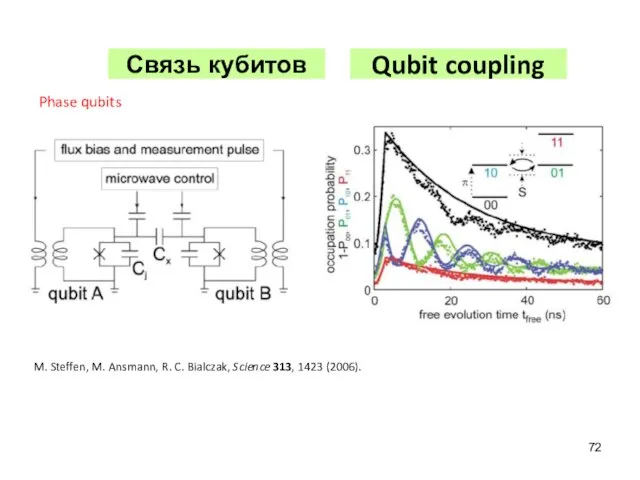
- 72. Qubit coupling M. Steffen, M. Ansmann, R. C. Bialczak, Science 313, 1423 (2006). Phase qubits Связь
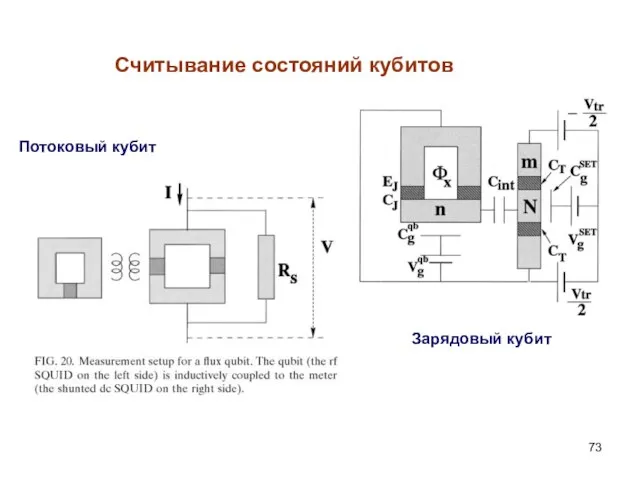
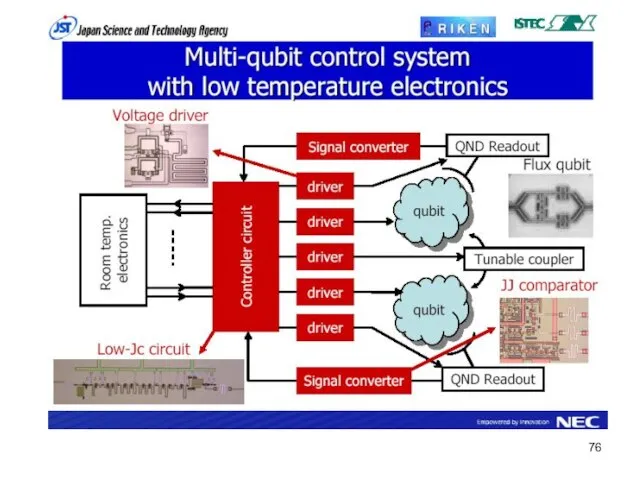
- 73. Считывание состояний кубитов Потоковый кубит Зарядовый кубит
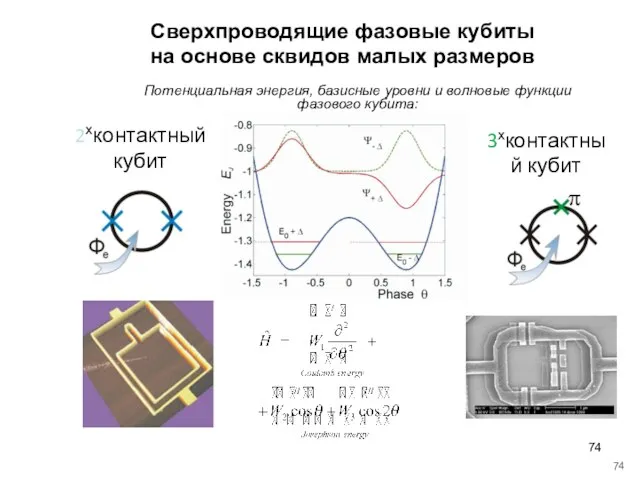
- 74. Сверхпроводящие фазовые кубиты на основе сквидов малых размеров Потенциальная энергия, базисные уровни и волновые функции фазового
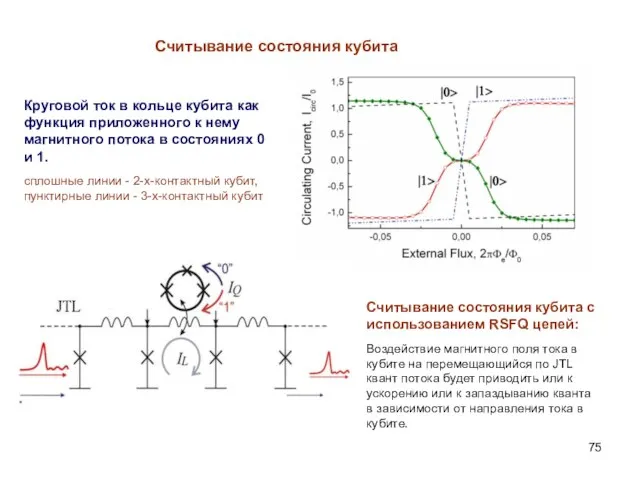
- 75. Круговой ток в кольце кубита как функция приложенного к нему магнитного потока в состояниях 0 и
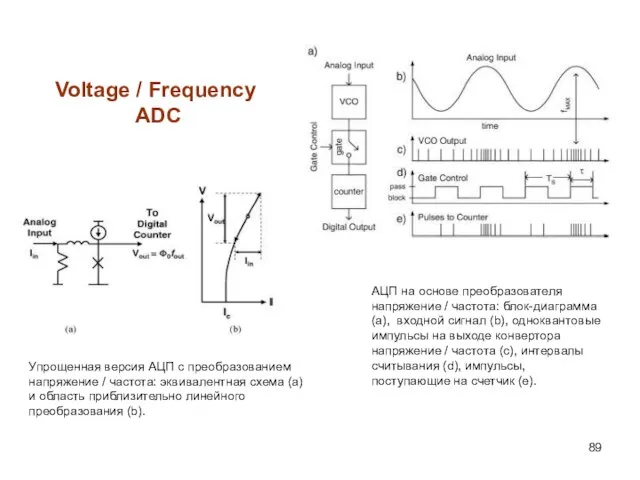
- 89. Voltage / Frequency ADC Упрощенная версия АЦП с преобразованием напряжение / частота: эквивалентная схема (а) и
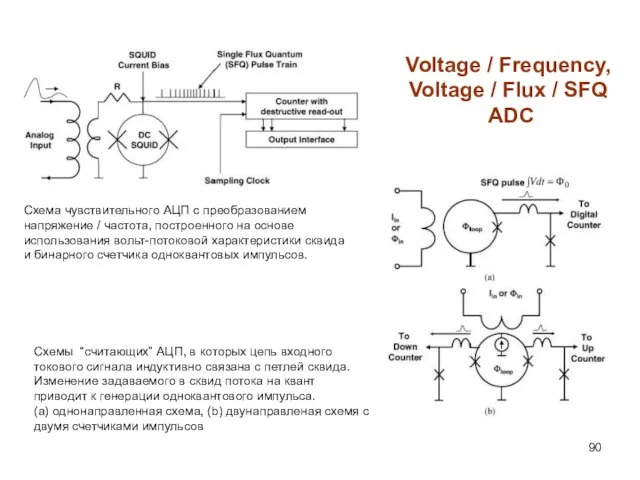
- 90. Voltage / Frequency, Voltage / Flux / SFQ ADC Схема чувствительного АЦП с преобразованием напряжение /
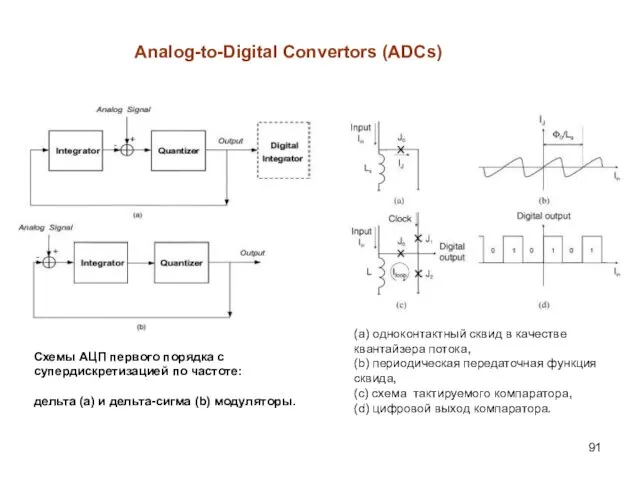
- 91. Analog-to-Digital Convertors (ADCs) Схемы АЦП первого порядка с супердискретизацией по частоте: дельта (a) и дельта-сигма (b)
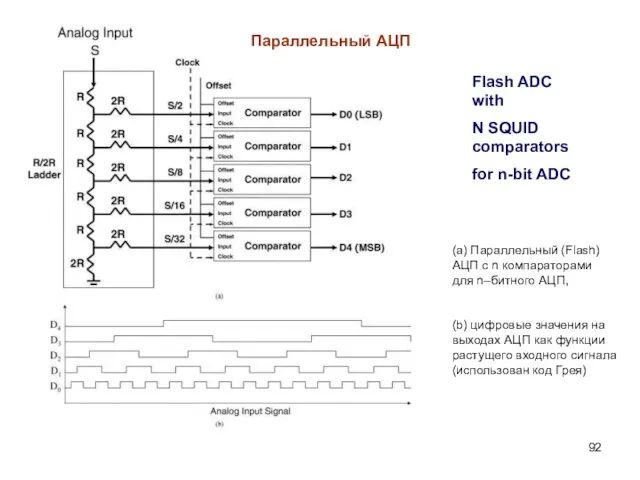
- 92. Flash ADC with N SQUID comparators for n-bit ADC (а) Параллельный (Flash) АЦП с n компараторами
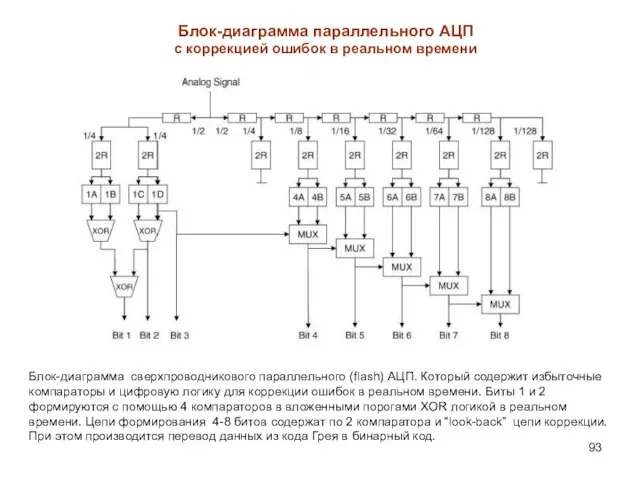
- 93. Блок-диаграмма сверхпроводникового параллельного (flash) АЦП. Который содержит избыточные компараторы и цифровую логику для коррекции ошибок в
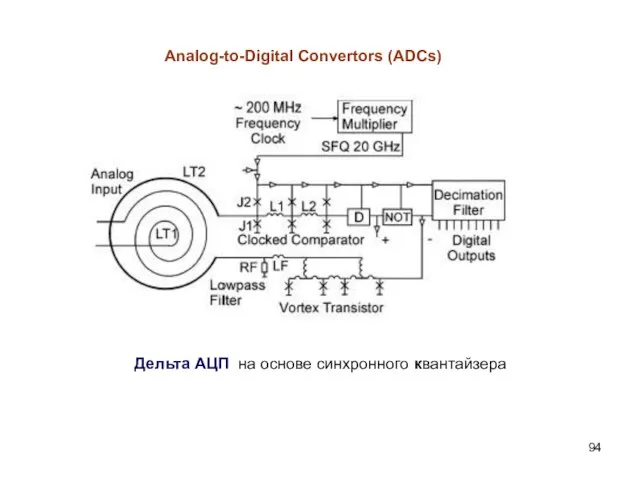
- 94. Analog-to-Digital Convertors (ADCs) Дельта АЦП на основе синхронного квантайзера
- 95. Analog-to-Digital Convertors (ADCs) Чип 5 х 5 мм, содержащий дельта АЦП с дельта модулятором и цифровым
- 106. Скачать презентацию



































 Презентация на тему Строение и функции кожи
Презентация на тему Строение и функции кожи  Зеленая аптека
Зеленая аптека Человек и искусство
Человек и искусство Культура России в первой половине 19 века
Культура России в первой половине 19 века Паровые машины. Паровой двигатель Уатта.
Паровые машины. Паровой двигатель Уатта. 22 сентября 2009 г. Управление ремонтами в энергетике – в чем эффект? Дятлов Сергей Николаевич.
22 сентября 2009 г. Управление ремонтами в энергетике – в чем эффект? Дятлов Сергей Николаевич. Пуговичный и заклепочный полуавтомат
Пуговичный и заклепочный полуавтомат Исследовательская деятельность учащихся как компонент формирования креативной личности
Исследовательская деятельность учащихся как компонент формирования креативной личности Samsung GALAXY Note
Samsung GALAXY Note Презентация на тему Олонец – трижды столица
Презентация на тему Олонец – трижды столица Школьные оценки
Школьные оценки Аксиома параллельных прямых
Аксиома параллельных прямых Pravo_prezentatsia_1
Pravo_prezentatsia_1 Цвет. Основы цветоведения. Виртуальная экскурсия в музей. 6 класс (1)
Цвет. Основы цветоведения. Виртуальная экскурсия в музей. 6 класс (1) ОП по Гагинскому району МО МВД России Большеболдинский: история, сегодняшнее состояние и перспективы развития
ОП по Гагинскому району МО МВД России Большеболдинский: история, сегодняшнее состояние и перспективы развития Романтизм в искусстве
Романтизм в искусстве Шоколадная Жизнь
Шоколадная Жизнь Автомобили пожарные рукавные
Автомобили пожарные рукавные Спектр сигнала. Свойства ДПФ
Спектр сигнала. Свойства ДПФ Правописание окончаний имён прилагательных мужского и среднего рода
Правописание окончаний имён прилагательных мужского и среднего рода Примеры Циклических колебаний Численности Животных и растений
Примеры Циклических колебаний Численности Животных и растений Проектная работа ученицы 3 "А"класса МОУ СОШ № 20 с.Шепси Ивановой Ларисы
Проектная работа ученицы 3 "А"класса МОУ СОШ № 20 с.Шепси Ивановой Ларисы Система работы по подготовке к ЕГЭ (русский язык)
Система работы по подготовке к ЕГЭ (русский язык) Введение в оториноларингологию
Введение в оториноларингологию Дон Аминадо. (Шполянский Аминад Петрович)
Дон Аминадо. (Шполянский Аминад Петрович) Деятельностный подход в обучении на уроках математики
Деятельностный подход в обучении на уроках математики Современные аспекты панкреатодуоденальной резекции (ПДР) Докладчик студент VI курса 603-А группы Рыжкин В.В.
Современные аспекты панкреатодуоденальной резекции (ПДР) Докладчик студент VI курса 603-А группы Рыжкин В.В. ЄБРР Фінансування проектів теплопостачання в Україні 20 вересня 2011
ЄБРР Фінансування проектів теплопостачання в Україні 20 вересня 2011