Содержание
- 3. Актуальность: В современном мире множество отраслей, связанных с химией, например такие, как пищевая, фармацевтическая, тяжёлая промышленность
- 4. Цели и задачи: 1. Выяснить, какие математические способы позволяют быстро решать задачи на смешивание (сплавление) веществ.
- 5. Теоретические основы решения задач «на смеси, сплавы, растворы» Перед тем, как приступить к объяснению различных способов
- 6. типы задач на вычисление концентрации; на вычисление количества чистого вещества в смеси (или сплаве); на вычисление
- 7. Способы решения задач с помощью таблиц с помощью схем старинным арифметическим способом алгебраическим способом с помощью
- 8. Задача 1. Сколько нужно добавить воды в сосуд, содержащий 200 г 70 % -го раствора уксусной
- 9. Задача 2. Имеется два сплава меди и свинца. Один сплав содержит 15% меди, а другой 65%
- 10. Задача 3 Свежие абрикосы содержат 80 % воды по массе, а курага (сухие абрикосы) – 12
- 11. Замечательный русский математик и педагог Леонтий Филиппович Магницкий (1669—1739) фамилию свою получил (1700) от Петра I
- 12. Задача 4 При смешивании 5% -ного раствора кислоты с 40% -ным раствором кислоты получили 140 г
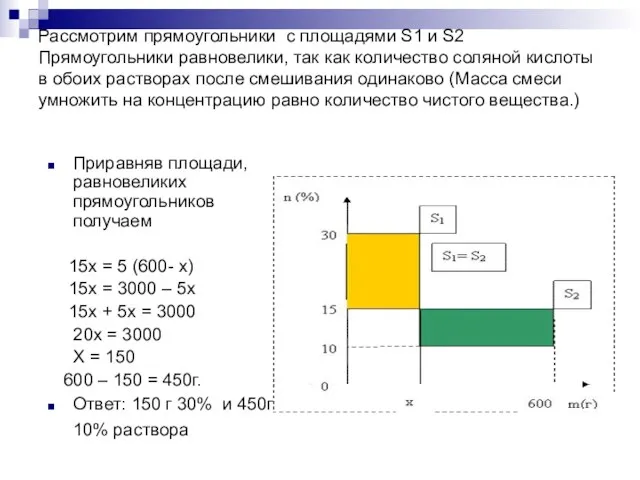
- 13. Задача 6 Смешали 30%-й раствор соляной кислоты с 10%-ым раствором и получили 600 г 15%-го раствора.
- 14. Рассмотрим прямоугольники с площадями S1 и S2 Прямоугольники равновелики, так как количество соляной кислоты в обоих
- 16. Выводы Изучили способы решения задач на смеси и сплавы, расширив свои знания по математике Выяснили, что
- 18. Скачать презентацию














 Реформа языка Карамзина
Реформа языка Карамзина Варианты расчета бонуса за два месяца
Варианты расчета бонуса за два месяца Эксплуатация автомобильного транспорта
Эксплуатация автомобильного транспорта Государство в политической системе
Государство в политической системе ИСТОРИЯ СПИЧЕК
ИСТОРИЯ СПИЧЕК Презентация на тему Растения-индикаторы
Презентация на тему Растения-индикаторы Мышление как психический процесс. Виды и формы мышления. 4 формата мышления
Мышление как психический процесс. Виды и формы мышления. 4 формата мышления Субъекты правовых отношений. Правовое положение лиц
Субъекты правовых отношений. Правовое положение лиц скульптура «Под одними звездами» ("Unter den gleichen Sternen")
скульптура «Под одними звездами» ("Unter den gleichen Sternen") Виды гимнастики
Виды гимнастики Hilton Hotels & Resorts
Hilton Hotels & Resorts Шар. Елка. Снеговик
Шар. Елка. Снеговик Обзор православной литературы Доброе слово для малых ребят
Обзор православной литературы Доброе слово для малых ребят Водные маршруты
Водные маршруты Презентация на тему Василий Тёркин
Презентация на тему Василий Тёркин  Технология приготовления пиццы
Технология приготовления пиццы Мир в свечах Выполнила: Плаксунова Людмила МОУ СОШ №4 Руководитель: Чуприна Т.В.
Мир в свечах Выполнила: Плаксунова Людмила МОУ СОШ №4 Руководитель: Чуприна Т.В. "Поле - чудес" по произведениям К.И. Чуковского
"Поле - чудес" по произведениям К.И. Чуковского PURE_THERAPY_Bezuprechnaya_idealno_ochischennaya_kozha
PURE_THERAPY_Bezuprechnaya_idealno_ochischennaya_kozha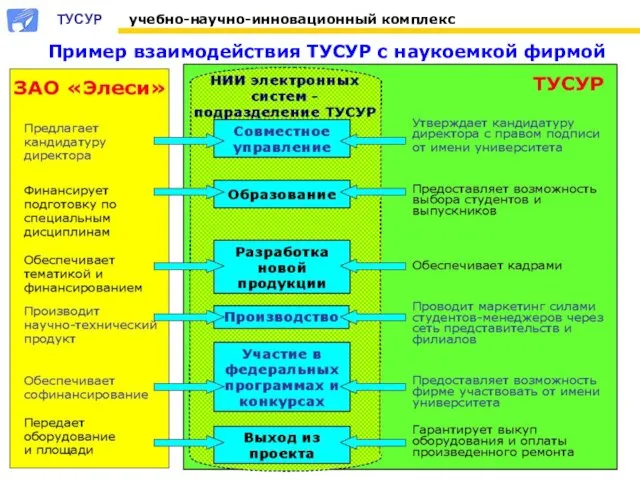 Пример взаимодействия ТУСУР с наукоемкой фирмой
Пример взаимодействия ТУСУР с наукоемкой фирмой Введение в менеджмент
Введение в менеджмент Австралия
Австралия Who should be the first ?
Who should be the first ? Велосипедный туризм
Велосипедный туризм Музей восстания машин
Музей восстания машин Презентация "Художники пореформенной России" - скачать презентации по МХК
Презентация "Художники пореформенной России" - скачать презентации по МХК Хочу отдыхать
Хочу отдыхать Сенситивные периоды человека (методика Марии Монтессори)
Сенситивные периоды человека (методика Марии Монтессори)