Развитие конструктивного мышления учащихся при решении задач на нахождение площади, периметра, объема геометрических объектов

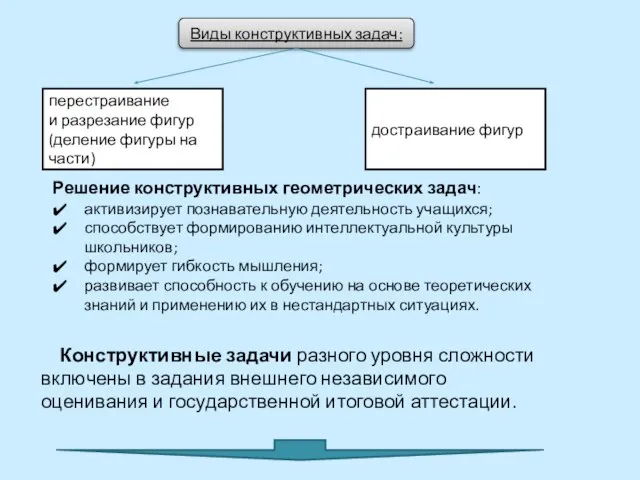
Виды конструктивных задач:
Решение конструктивных геометрических задач:
активизирует познавательную деятельность учащихся;
способствует формированию интеллектуальной культуры школьников;
формирует гибкость мышления;
развивает способность к обучению на основе теоретических знаний и применению их в нестандартных ситуациях.
Конструктивные задачи разного уровня сложности включены в задания внешнего независимого оценивания и государственной итоговой аттестации.
перестраивание
и разрезание фигур (деление фигуры на части)
достраивание фигур

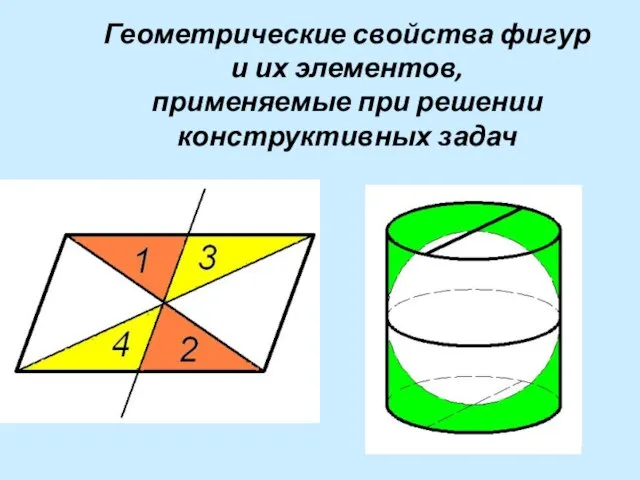
Геометрические свойства фигур
и их элементов,
применяемые при решении
конструктивных задач

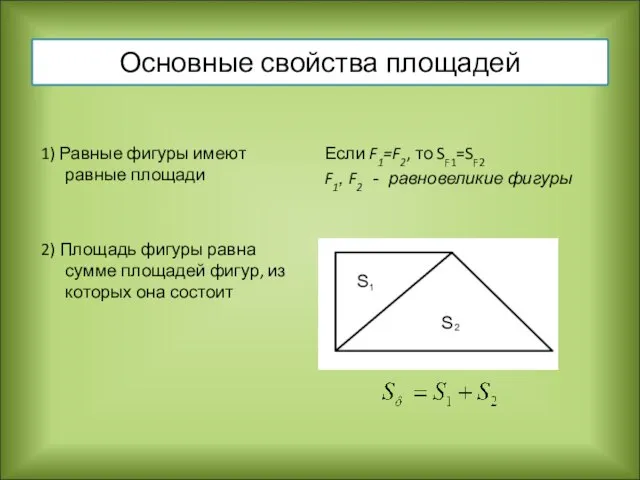
Основные свойства площадей
1) Равные фигуры имеют равные площади
2) Площадь фигуры равна сумме площадей фигур, из которых она состоит
Если F1=F2, то SF1=SF2
F1, F2 - равновеликие фигуры

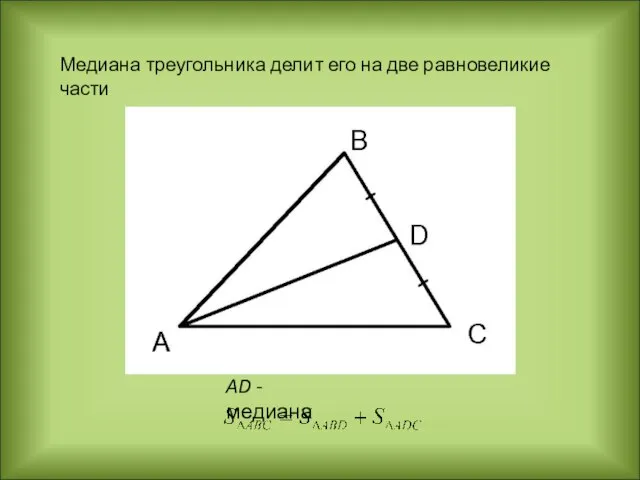
Медиана треугольника делит его на две равновеликие части
AD - медиана

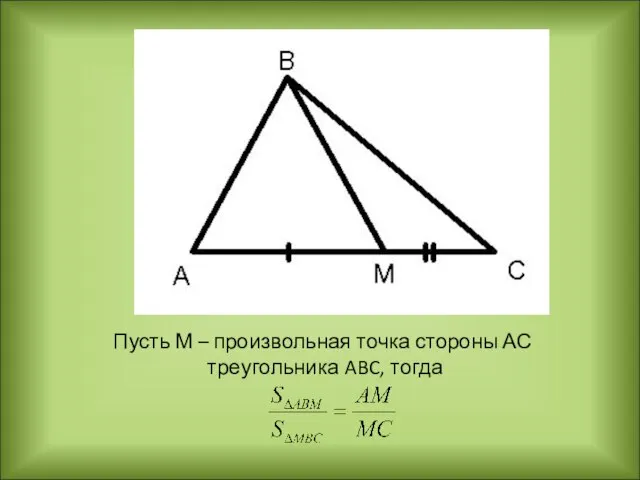
Пусть М – произвольная точка стороны АС
треугольника ABC, тогда

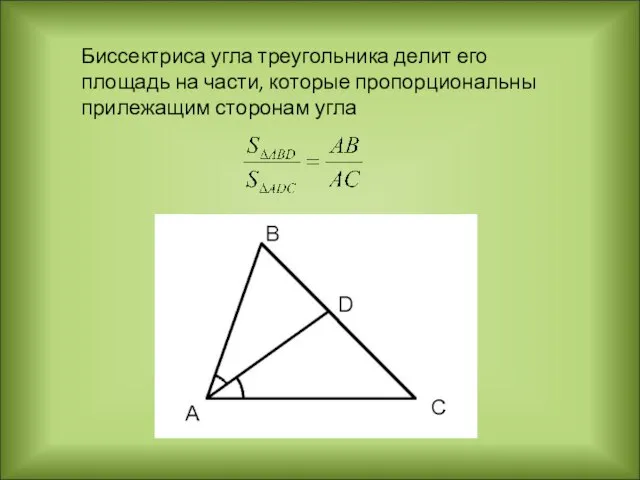
Биссектриса угла треугольника делит его площадь на части, которые пропорциональны прилежащим сторонам угла

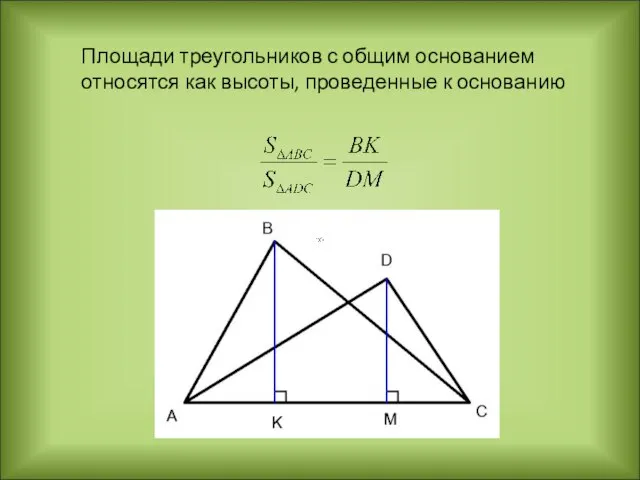
Площади треугольников с общим основанием относятся как высоты, проведенные к основанию

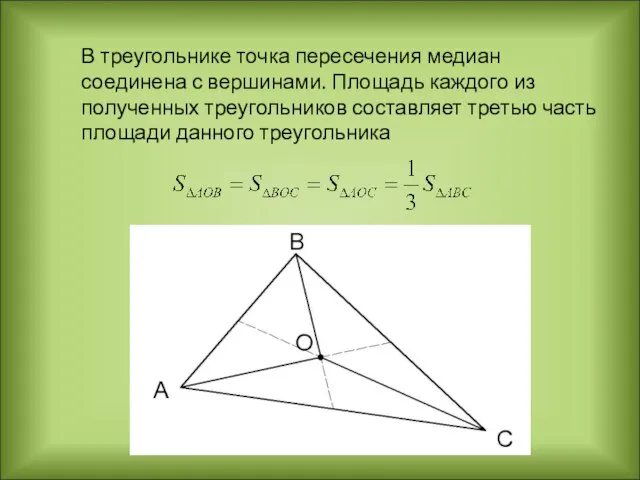
В треугольнике точка пересечения медиан соединена с вершинами. Площадь каждого из полученных треугольников составляет третью часть площади данного треугольника

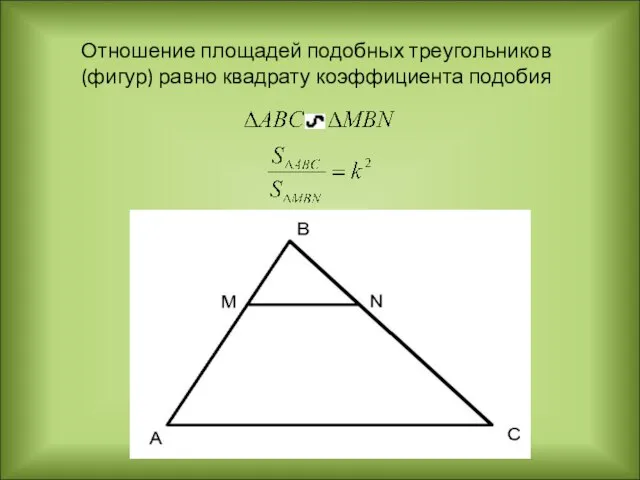
Отношение площадей подобных треугольников (фигур) равно квадрату коэффициента подобия

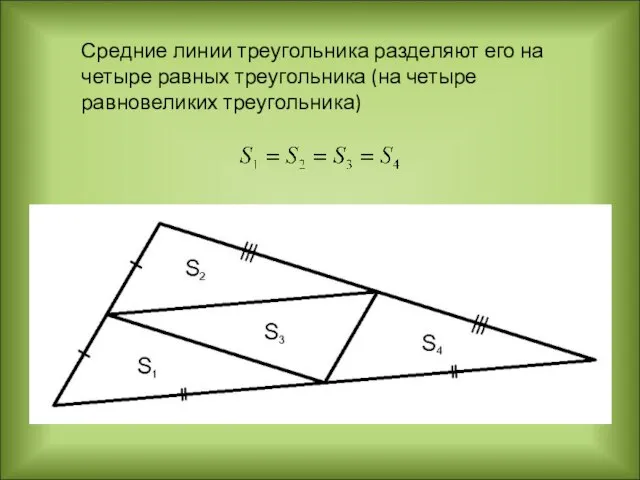
Средние линии треугольника разделяют его на четыре равных треугольника (на четыре равновеликих треугольника)

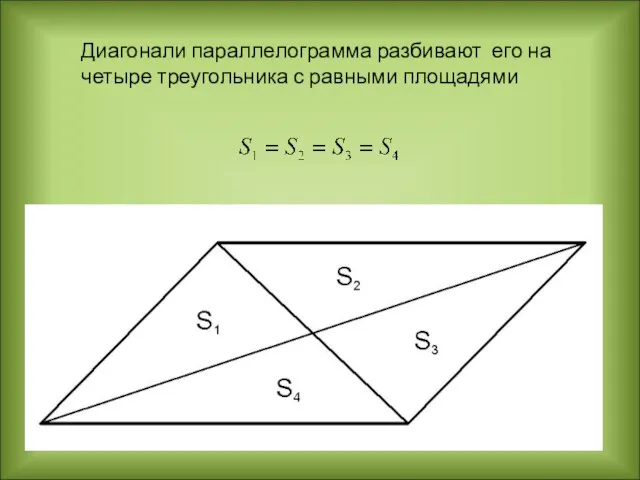
Диагонали параллелограмма разбивают его на четыре треугольника с равными площадями

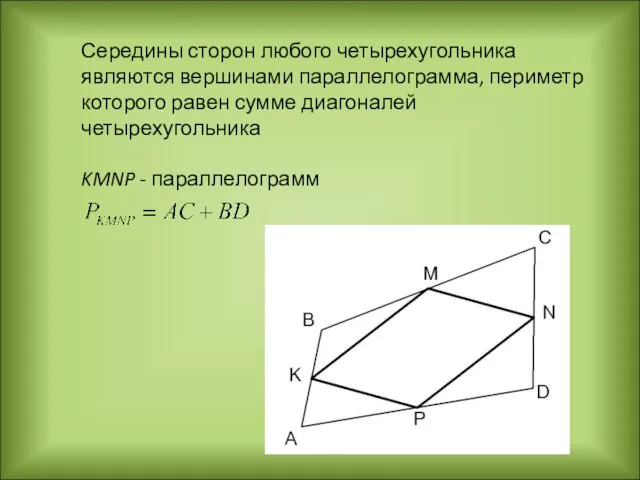
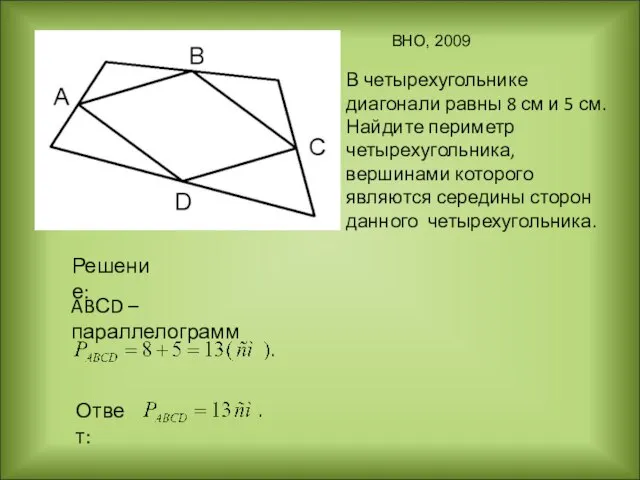
Середины сторон любого четырехугольника являются вершинами параллелограмма, периметр которого равен сумме диагоналей четырехугольника
KMNP - параллелограмм

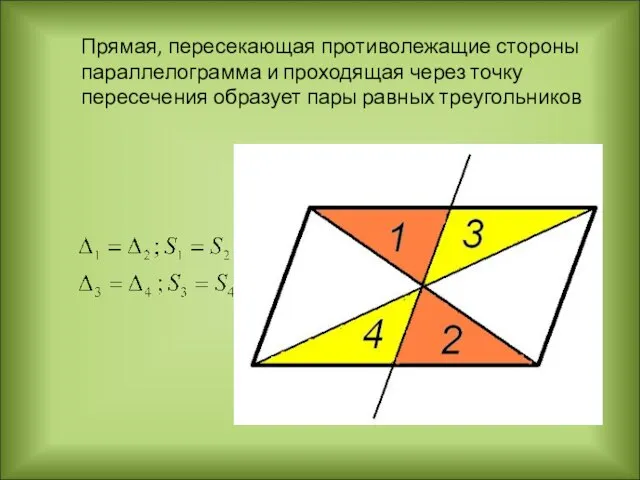
Прямая, пересекающая противолежащие стороны параллелограмма и проходящая через точку пересечения образует пары равных треугольников

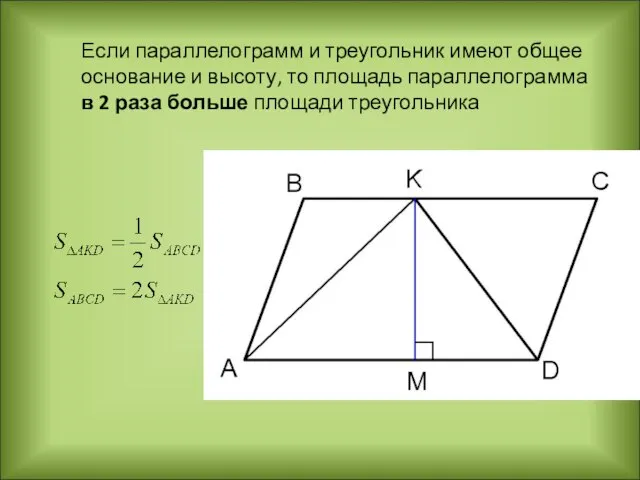
Если параллелограмм и треугольник имеют общее основание и высоту, то площадь параллелограмма
в 2 раза больше площади треугольника

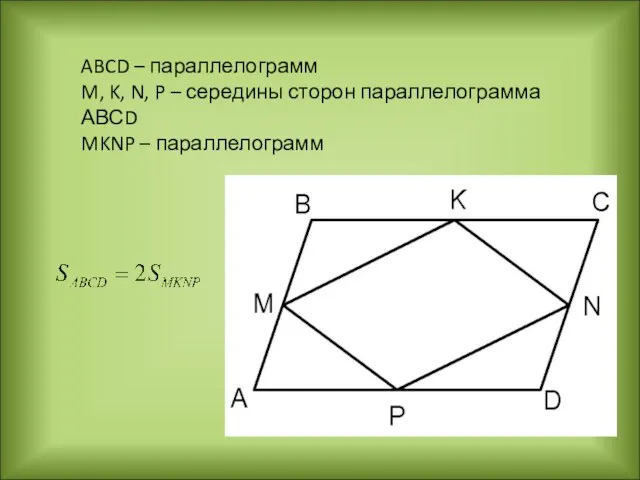
ABCD – параллелограмм
M, K, N, P – середины сторон параллелограмма АВСD
MKNP – параллелограмм

Точка М – середина стороны квадрата ABCD. Площадь заштрихованной части равна
7 см2. Найти площадь всего квадрата.
Решение:
Дополнительное построение:
АС – диагональ. ∆ABC, АМ – медиана.
Ответ:
ВНО, 2010

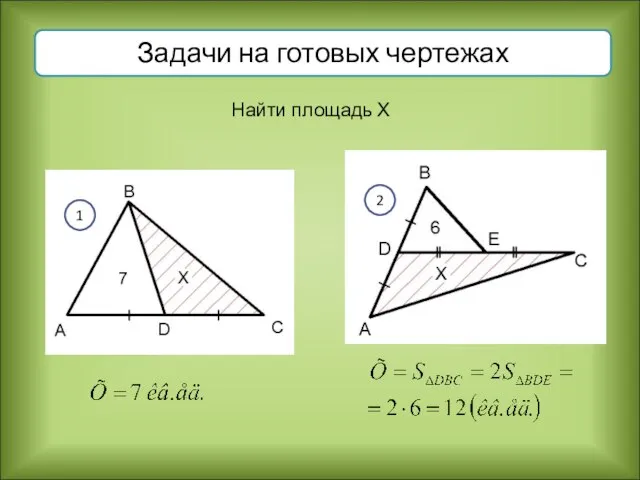
Найти площадь Х
1
2
Задачи на готовых чертежах

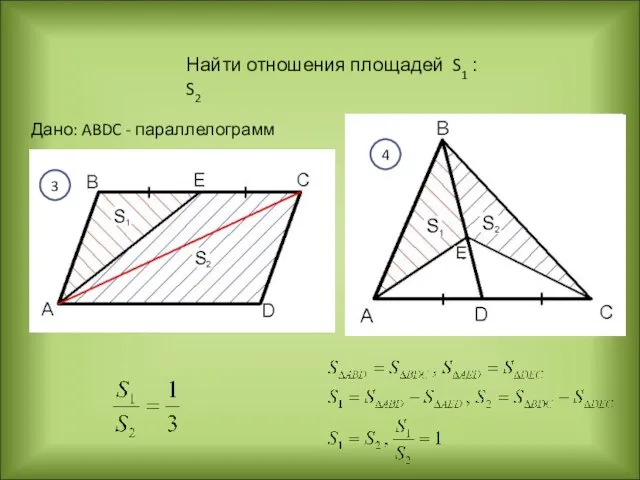
Найти отношения площадей S1 : S2
3
4
Дано: ABDC - параллелограмм
4

Одна из сторон треугольника равна
20 см, а медианы, проведенные к двум другим сторонам равны 18 см и 24 см. Найти площадь треугольника.
Решение:
1)
Ответ:
2)

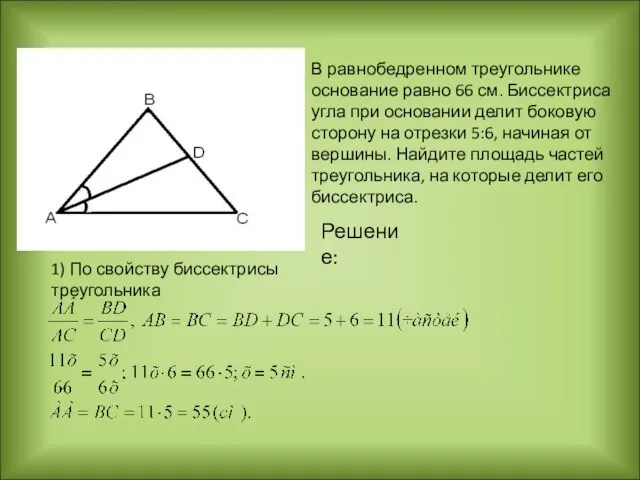
В равнобедренном треугольнике основание равно 66 см. Биссектриса угла при основании делит боковую сторону на отрезки 5:6, начиная от вершины. Найдите площадь частей треугольника, на которые делит его биссектриса.
Решение:
1) По свойству биссектрисы треугольника

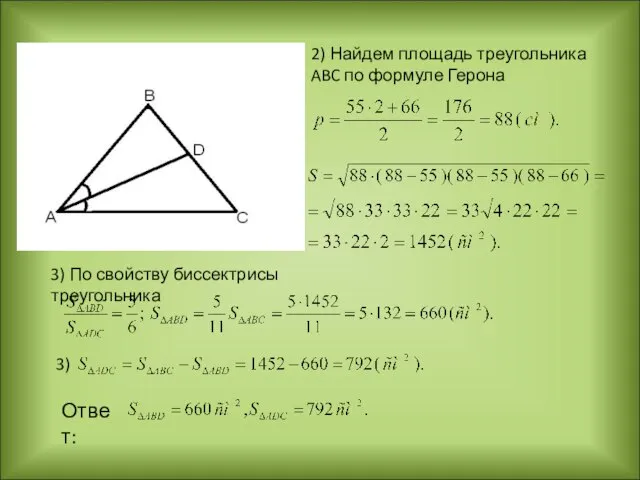
2) Найдем площадь треугольника ABC по формуле Герона
3) По свойству биссектрисы треугольника
3)
Ответ:

MK – средняя линия треугольника ABC. Площадь треугольника ABC равна 20 см2. Найдите площадь четырехугольника ABMK.
Решение:
1) MK || AB по свойству средней линии треугольника.
Ответ:
2)
ВНО, 2008

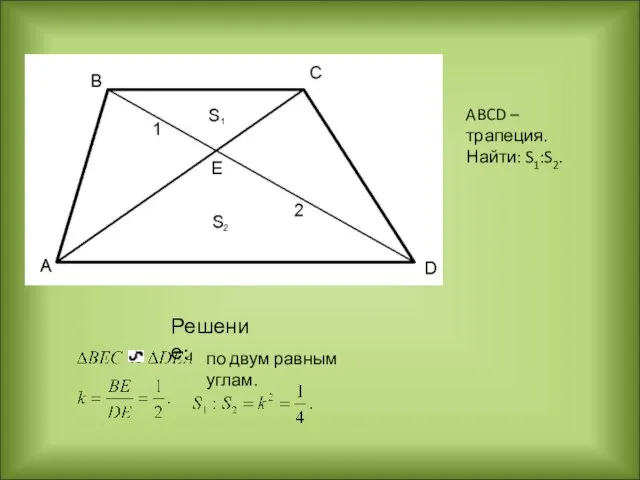
Решение:
по двум равным углам.
ABCD – трапеция.
Найти: S1:S2.

В прямоугольнике ABCD прямые m и n проходят через точку пересечения диагоналей. Площадь фигуры, которая состоит из трех закрашенных треугольников, равна 12 см2.
Вычислите площадь прямоугольника ABCD.
Решение:
Ответ:
ВНО, 2010

На рисунке изображен прямоугольник ABCD и равносторонний треугольник ABK, периметры которых соответственно равны 20 см и 12 см. Найдите периметр пятиугольника AKBCD.
Решение:
Ответ:
∆ABK - равносторонний
ВНО, 2010

На рисунке изображен квадрат ABCD и треугольник BKC, периметры которых соответственно равны 24 см и 20 см. Найдите периметр пятиугольника ABKCD.
Решение:
Ответ:
, ABСD – квадрат
ВНО, 2010

В четырехугольнике диагонали равны 8 см и 5 см. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
Решение:
Ответ:
ABСD – параллелограмм
ВНО, 2009

Точка K лежит на стороне DC параллелограмма ABCD. Известно, что угол AKB прямой, АК = 8 см,
KB = 5 см. Найдите площадь параллелограмма.
Решение:
Ответ:
ВНО, 2008

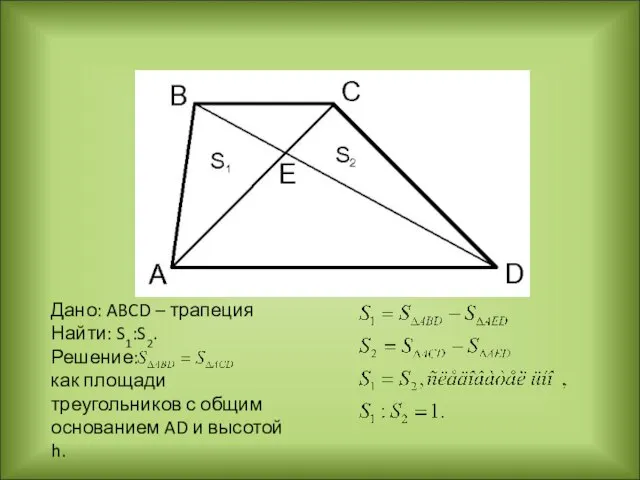
Дано: ABCD – трапеция
Найти: S1:S2.
Решение:
как площади треугольников с общим основанием AD и высотой h.

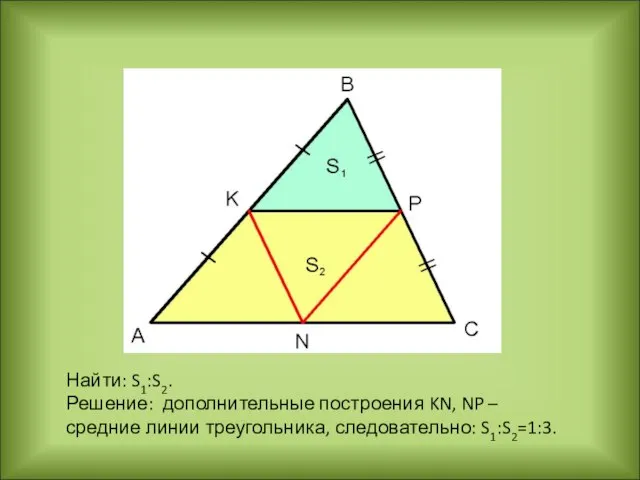
Найти: S1:S2.
Решение: дополнительные построения KN, NP – средние линии треугольника, следовательно: S1:S2=1:3.

№256 Геометрия, 10 класс, Бевз Г.П, и др,
профильный уровень
В треугольнике ABC через точку М – середину стороны АВ – проведена плоскость α, α||BC, α AC = N. Найдите: а) ВС, если MN=a; б) SBMNC:SMAN.

Из цилиндра выточен конус так, что его основание совпадает с одним из оснований цилиндра, а вершина с центром другого основания цилиндра. Найдите отношение объема сточенной части цилиндра к объему конуса.
Решение:
ВНО, 2010

Объем куба ABCDA1B1C1D1 равен 216 см3. Найдите объем пирамиды D1ACD.
Решение:
Ответ:
ВНО, 2010

В сосуд цилиндрической формы, наполненный водой доверху, положили металлический шар, который касается дна и стенок. Определите отношение объема воды, которая осталась в сосуде, к объему воды, которая вылилась.
Решение:
V1 – объем воды, которая осталась;
V2 – объем вылившейся воды.
ВНО, 2008