Содержание
- 2. Рекурсия – подпрограмма, которая в своем теле вызывает сама себя. В языке Паскаль существует два вида
- 3. Функции Подпрограмма — часть программы, оформленная в виде отдельной синтаксической конструкции и снабжённая именем (самостоятельный программный
- 4. У функций и процедур существуют параметры (переменные, которые передают какое - либо значение). Они бывают двух
- 5. Задача. Вывести цифры числа в обратном порядке. Рассмотрим алгоритм решения: Возьмем число 3096. Последняя цифра -
- 6. Задача. Найти первых n чисел Фибоначчи. Числа Фибоначчи — числовая последовательность, первые два элемента которой равны
- 7. Найти первых n чисел Фибоначчи. Program Fib; Var i,n:Integer; {Функция поиска f-ого числа Фибоначчи} Function fib(f:integer):integer;
- 9. Алгоритм решения: Допустим у нас 3 кубика. Берем все кубики и выкладываем в 1 слой –
- 11. Скачать презентацию
Слайд 2Рекурсия – подпрограмма, которая в своем теле вызывает сама себя.
В языке
Рекурсия – подпрограмма, которая в своем теле вызывает сама себя.
В языке

Program ИмяПрограммы;
VAR … // раздел описания переменных главной программы;
procedure ИмяПроцедуры;
var …
begin
… //Тело процедуры
end;
begin
… //тело главной программы
end.
Слайд 3Функции
Подпрограмма — часть программы, оформленная в виде отдельной синтаксической конструкции и снабжённая
Функции
Подпрограмма — часть программы, оформленная в виде отдельной синтаксической конструкции и снабжённая
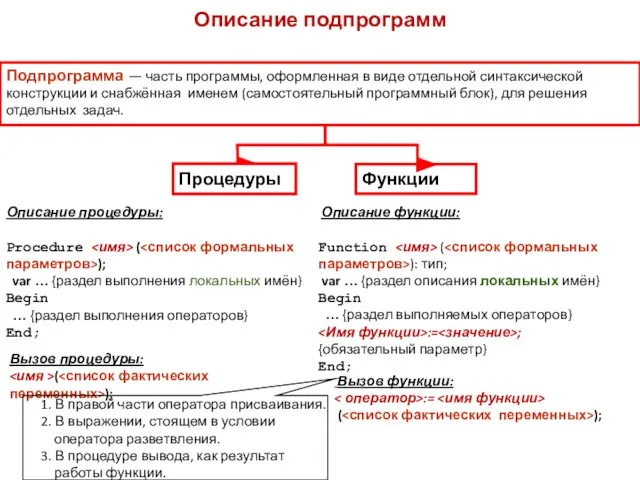
Описание процедуры:
Procedure <имя> (<список формальных параметров>);
var … {раздел выполнения локальных имён}
Begin
… {раздел выполнения операторов}
End;
Описание функции:
Function <имя> (<список формальных параметров>): тип;
var … {раздел описания локальных имён}
Begin
… {раздел выполняемых операторов}
<Имя функции>:=<значение>; {обязательный параметр}
End;
Вызов процедуры:
<имя >(<список фактических переменных>);
Вызов функции:
< оператор>:= <имя функции>
(<список фактических переменных>);
1. В правой части оператора присваивания.
2. В выражении, стоящем в условии оператора разветвления.
3. В процедуре вывода, как результат работы функции.
Описание подпрограмм
Процедуры
Слайд 4 У функций и процедур существуют параметры (переменные, которые передают какое - либо
У функций и процедур существуют параметры (переменные, которые передают какое - либо

1) Формальные - те, которые находятся в описании подпрограммы
2) Фактические - те, которые передаются из основной программы в функцию или процедуру.
Фактические параметры должны соответствовать формальным по количеству, порядку следования и типу.
Также у подпрограммы существую переменные, с которыми она в дальнейшем работает. Они делятся опять же на два типа:
1) Глобальные переменные, то есть действующие во всей программе
2) Локальные - те, которые действуют только в процедуре или функции
В языке программирования Pascal рекурсивностью могут обладать как функции, так и процедуры.
Наличие условия в теле рекурсивной функции (или процедуры), при котором она больше себя не будет вызывать, очень важно. В противном случае, как и в ситуации с циклами, может произойти так называемое зацикливание.
При каждом рекурсивном вызове создается новое множество локальных переменных. То есть переменные, расположенные вне вызываемой функции, не изменяются.
Слайд 5Задача. Вывести цифры числа в обратном порядке.
Рассмотрим алгоритм решения:
Возьмем число 3096.
Задача. Вывести цифры числа в обратном порядке.
Рассмотрим алгоритм решения:
Возьмем число 3096.

Воспользуемся рекурсивной процедурой rever:
procedure rever (n: integer); {n – искомое число, переданное в процедуру rever, формальная переменная}
begin
write (n mod 10); {выводим текущий остаток от деления на 10 - цифру}
if (n div 10)<>0 then rever (n div 10); {проверяем после деления останется число и передаем новое число в процедуру rever – рекурсивный вызов}
end;
begin
rever (3096); {вызов процедуры из тела основной программы, 3096 – фактическая переменная}
readln;
end.
Работа процедуры:
1. Мы передаем число 3096.
2. Процедура rever выводит на экран остаток от деления на 10. Это число 6.
3 Переход на новую строку не происходит, т.к. используется write.
4 Проверяется условие того, что 3096 при деление нацело на 10 больше нуля.
5 Вызывается rever с фактическим параметром, равным 309.
6 Вторая запущенная процедура выводит на экран цифру 9 и запускает третью процедуру с параметром 30.
7. Третья процедура выводит 0 и вызывает четвертый rever с 3 в качестве параметра.
8. Четвертая процедура выводит 3 на экран и ничего больше не вызывает, т.к. условие (3 div 10) <> 0 ложно.
9. Четвертая процедура завершается и передает управление третьей. Третья процедура завершается и передает управление второй. Вторая процедура завершается и передает управление первой. Первая процедура завершается и передает управление в основную ветку программы.
В итоге, процедура rever была вызвана четыре раза, хотя из основной программы к ней было единственное обращение.
Слайд 6Задача. Найти первых n чисел Фибоначчи.
Числа Фибоначчи — числовая последовательность, первые два
Задача. Найти первых n чисел Фибоначчи.
Числа Фибоначчи — числовая последовательность, первые два

Вывод программы должен выглядеть следующим образом: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, …
Алгоритм решения: Допустим fn – одно из чисел Фибоначчи, тогда f1=1, f2=1, f3= f2+f1, f4= f3+f2, тогда fn =fn-1+fn-2.
Пусть рекурсивная функция поиска числа Фибоначчи fib(n). Тогда f1 и f2 будут условием выхода из рекурсии:
If (f=1) or (f=2) then fib:=1,
а для получения нового числа Фибоначчи будем самой рекурсивной функции присваивать сумму вызовов рекурсии со значениями n-1 и n-2:
fib:=fib(n-1)+fib(n-2);
Осталось создать основную программу и прописать ряд для чисел Фибоначчи.
Слайд 7Найти первых n чисел Фибоначчи.
Program Fib;
Var i,n:Integer;
{Функция поиска f-ого числа Фибоначчи}
Function fib(f:integer):integer;
Begin
If
Найти первых n чисел Фибоначчи.
Program Fib;
Var i,n:Integer;
{Функция поиска f-ого числа Фибоначчи}
Function fib(f:integer):integer;
Begin
If

End;
Begin
Readln(n);
For i:=1 to n do Write(fib(i):4);
Readln;
End.
Слайд 9Алгоритм решения:
Допустим у нас 3 кубика. Берем все кубики и выкладываем
Алгоритм решения:
Допустим у нас 3 кубика. Берем все кубики и выкладываем


 Пасха
Пасха Подвеска. Мобиль Бабочки
Подвеска. Мобиль Бабочки Паттерн Команда
Паттерн Команда Показательная функция
Показательная функция Проектирование СКС коттеджного участка из бруса
Проектирование СКС коттеджного участка из бруса Морфология и орфография
Морфология и орфография Features of lerning process
Features of lerning process Построение натюрморта
Построение натюрморта Общественные центры – возможность для СО НКО получить помещение в безвозмездное пользование
Общественные центры – возможность для СО НКО получить помещение в безвозмездное пользование О состоянии образовательного процесса МОУ СОШ № 29 : итоги 2 четверти 2011-2012 уч. г.
О состоянии образовательного процесса МОУ СОШ № 29 : итоги 2 четверти 2011-2012 уч. г. Формирование универсальных учебных действий на уроках физической культуры
Формирование универсальных учебных действий на уроках физической культуры Урок №11
Урок №11 3_2_Elementy_upravlenia
3_2_Elementy_upravlenia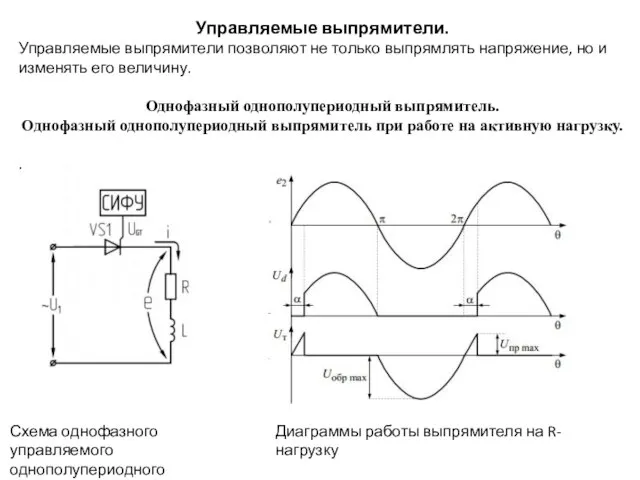 Управляемые выпрямители (тема 4)
Управляемые выпрямители (тема 4) Реактивная система залпового огня Смерч
Реактивная система залпового огня Смерч Гроза. Молния
Гроза. Молния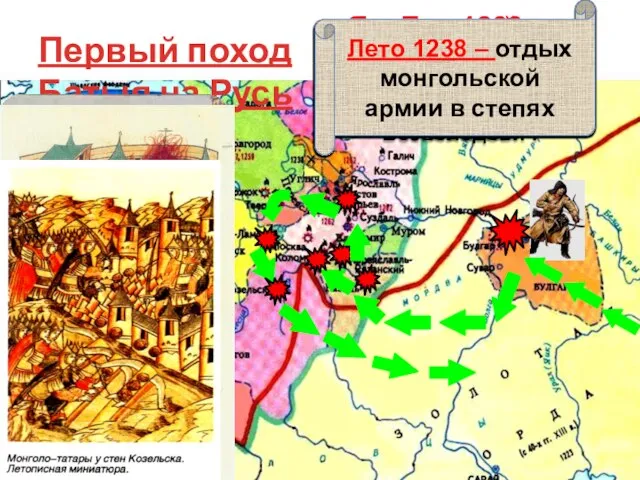 Первый поход Батыя на Русь
Первый поход Батыя на Русь Жиры
Жиры Аддис - уникальная кофейня
Аддис - уникальная кофейня Презентация на тему Уголовно-процессуальное право
Презентация на тему Уголовно-процессуальное право  Сравнительный анализ энергоемкости промышленной продукции
Сравнительный анализ энергоемкости промышленной продукции Тема 4 .2 10 класс
Тема 4 .2 10 класс Презентация на тему Тип профессий
Презентация на тему Тип профессий  В мире северной фразеологии
В мире северной фразеологии Я - учитель
Я - учитель Мы за жизнь ВЫПОЛНИЛА УЧЕНИЦА 9А КЛАССА Кознова Валерия.
Мы за жизнь ВЫПОЛНИЛА УЧЕНИЦА 9А КЛАССА Кознова Валерия. «Донорство в Озинском районе»
«Донорство в Озинском районе» Болезни кровеносной системы
Болезни кровеносной системы