Слайд 2Содержание
Теория: - определение
- свойства
- способы решения
Задания для решения вместе
Задания

для самостоятельной работы
Задания для работы в парах
Слайд 3 ТЕОРИЯ
Иррациональными называются неравенства, содержащие переменную под знаком корня
При решении иррациональных неравенств

надо находить ОДЗ, т.к. сделать проверку труднее
Если обе части неравенства не отрицательны, то их можно возвести в четную степень и знак неравенства при этом не изменится
Неравенство можно возвести в нечетную степень не проверяя не отрицательность левой части.
Слайд 4 ТЕОРИЯ
Основным методом решения иррациональных неравенств является сведение его к системе

неравенств или к совокупности систем неравенств.
Чаще всего используются следующие случаи:
А)
Слайд 7 Е)
то неравенство не имеет решения
Ж)

Слайд 9САМОСТОЯТЕЛЬНАЯ РАБОТА
1)
2)
Ответ: [-4;5]
Ответ:
![САМОСТОЯТЕЛЬНАЯ РАБОТА 1) 2) Ответ: [-4;5] Ответ:](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/318924/slide-8.jpg)
Слайд 10 РАБОТА В ПАРАХ
1)
2)
Ответ: (-∞;-1)u(9;+∞)
Ответ: (-1;0)u(3;4)




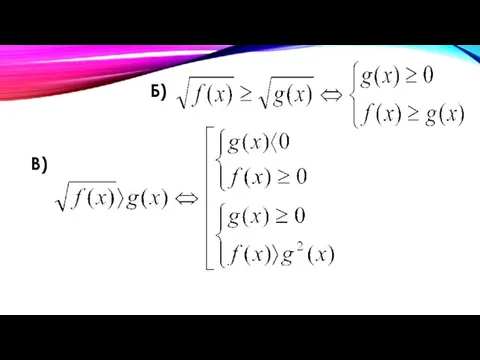
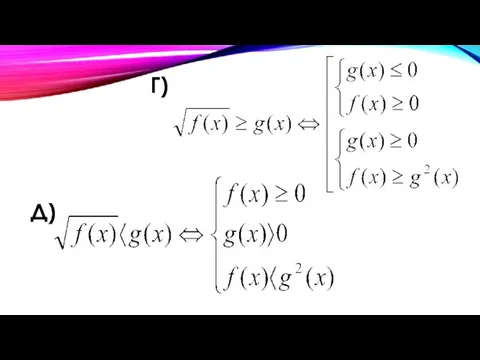


![САМОСТОЯТЕЛЬНАЯ РАБОТА 1) 2) Ответ: [-4;5] Ответ:](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/318924/slide-8.jpg)

 Влияние курения на организм человека
Влияние курения на организм человека Экономика впечатлений: Живая история в Хохловке
Экономика впечатлений: Живая история в Хохловке Электронное государство
Электронное государство Обучение на ПММ младшие курсы
Обучение на ПММ младшие курсы Основы рекламы: иллюстрация
Основы рекламы: иллюстрация Анатомия половой системы человека
Анатомия половой системы человека Векторное кодирование изображений
Векторное кодирование изображений Лучший детский сад2012 года
Лучший детский сад2012 года Основы инновационной деятельности
Основы инновационной деятельности Круговая тренировка из специальных упражнений для совершенствования нападающего
Круговая тренировка из специальных упражнений для совершенствования нападающего Опыт обучения финансовой грамотности взрослого населения
Опыт обучения финансовой грамотности взрослого населения Итоговая государственная аттестация выпускников 9-х классов
Итоговая государственная аттестация выпускников 9-х классов Опыт использования технологии блокчейн на российском рынке нефтепродуктов
Опыт использования технологии блокчейн на российском рынке нефтепродуктов Современные боевые средства вооруженной борьбы
Современные боевые средства вооруженной борьбы Меры поддержки энергосберегающих проектов на территории Республики Коми
Меры поддержки энергосберегающих проектов на территории Республики Коми Организационная структура Вооружённых сил. Виды Вооружённых сил. Рода войск. История их создания и предназначение
Организационная структура Вооружённых сил. Виды Вооружённых сил. Рода войск. История их создания и предназначение Искусство шрифта
Искусство шрифта Do’Doner. Размер
Do’Doner. Размер Системно – деятельностный метод обучения
Системно – деятельностный метод обучения Миграции населения России выполнила ученица 8А классаМОУ СОШ №133Гаврилюк анна
Миграции населения России выполнила ученица 8А классаМОУ СОШ №133Гаврилюк анна Конфликтность личности и ее проявление в общении
Конфликтность личности и ее проявление в общении Научно-исследовательская работа школьников
Научно-исследовательская работа школьников Профессиональная деятельность учителя английского языка МОУ СОШ №3 г. Козьмодемьянска Панкратовой Галины Владимировны
Профессиональная деятельность учителя английского языка МОУ СОШ №3 г. Козьмодемьянска Панкратовой Галины Владимировны Муниципальное общеобразовательное учреждение лингвистическая гимназия № 70
Муниципальное общеобразовательное учреждение лингвистическая гимназия № 70 Жизнь фракталов
Жизнь фракталов Изобразительное искусство в иллюстрациях
Изобразительное искусство в иллюстрациях Удмуртские народные сказки
Удмуртские народные сказки Лаборатория литературоведческих исследований филфака МаГУКафедра русской литературы ХХ века им. проф. Л.А. Заманского
Лаборатория литературоведческих исследований филфака МаГУКафедра русской литературы ХХ века им. проф. Л.А. Заманского