Слайд 2Решить уравнение
|х|=а При рассмотрении вариантов для параметра а необходимо помнить, что модуль

принимает только неотрицательные значения.
при а<0
решений нет
при а=0
|х|=0
х=0 – одно решение
при а>0
|х|=а, используем геометрический смысл модуля.
х=а, и х=–а т.е. два решения.
Ответ: при а<0, решений нет; при а=0, х=0; при а>0, х=а, и х=–а;
Слайд 3|ах+1|=а Параметр а может быть числом неотрицательным.
если а<0
|ах+1|=а нет решений.
если а=0
|0х+1|=0
|1|=0 нет

решений.
если а>0
|ах+1|=а, используя геометрический смысл модуля, решим два уравнения.
ах+1=а и ах+1=–а
ах=а–1 ах=–а–1
х=(а–1)/а х=–(а=1)/а
Ответ: при а<0, нет решений; при а=0, нет решений; а>0, х=(а–1)/а, х=–(а=1)/а;
Слайд 4|а–2х|=3 т.к. число 3>0, то используя геометрический смысл, рассмотрим два уравнения.
а–2х=3 и а–2х=–3
а–3=2х а+3=2х
2х=а–3 2х=а+3
х=(а–3)/2 х=(а+3)/2
т.е. при

любых значениях параметра а имеется два решения
Ответ: при а – любом, х=(а–3)/2, х=(а+3)/2;
Слайд 5|ах–а|=а, число а должно быть неотрицательным
если а<0, то уравнение не имеет решений
если

а=0, то уравнение принимает вид:
|0х–0|=0
|0|=0, т.е. х – любое число.
если а>0
|ах–а|=а, то рассмотрим два уравнения
ах–а=а и ах–а=–а
ах=а+а ах=–а+а
ах=2а ах=0
х=2а/а х=0/а
х=2 х=0
Ответ: при а<0, нет решений; при а=0, х – любое; при а>0, х=2, х=0;
Слайд 6a|х–1|=4 преобразуем уравнение
|х–1|=4/а рассмотрим случаи:
если а<0, то
4/а<0
|х–1|=4/а не имеет решений.
2) если

а=0, то 4/0 не имеет смысла.
|х–1|=4/а не имеет решений.
если а>0, то 4/а>0
|х–1|=4/а, используя геометрический смысл модуля, рассмотрим два уравнения.
х–1=4/а и х–1=–4/а
х=1+4/а х=1–4/а
Ответ: при а>0, решений нет; при а=0, решений нет; при a>0, х=1+4/а, х=1–4/а;





 А.Е. Суворов «Об итогах деятельности радиоэлектронного комплекса в 2007 году и основных задачах на 2008 год»
А.Е. Суворов «Об итогах деятельности радиоэлектронного комплекса в 2007 году и основных задачах на 2008 год» Сложение и вычитание натуральных чисел (5 класс)
Сложение и вычитание натуральных чисел (5 класс) Экономика и ее роль в жизни общества
Экономика и ее роль в жизни общества Игра-конкурс по информатике(2-4классы)
Игра-конкурс по информатике(2-4классы) Отдел контроля качества. ОКК ЕвроАвто
Отдел контроля качества. ОКК ЕвроАвто Мой край родной
Мой край родной Поезд в Пушкинские горы. Проект создания трансферного узла
Поезд в Пушкинские горы. Проект создания трансферного узла Ремёсла в России 17 – 18 вв
Ремёсла в России 17 – 18 вв Рассматриваемые вопросы Основы системного подхода Понятие предметной области (ПрО). Программа как модель ПрО Классы в Java: описание
Рассматриваемые вопросы Основы системного подхода Понятие предметной области (ПрО). Программа как модель ПрО Классы в Java: описание Из опыта работы методиста Томского областного института повышения квалификации и переподготовки работников образования
Из опыта работы методиста Томского областного института повышения квалификации и переподготовки работников образования Презентация на тему Простое осложнённое предложение
Презентация на тему Простое осложнённое предложение Родительское собрание : методика подготовки и проведения
Родительское собрание : методика подготовки и проведения Габдулла Тукай – Величайший татарский поэт
Габдулла Тукай – Величайший татарский поэт Семейство Лилейные
Семейство Лилейные Презентация на тему Художники 18 века
Презентация на тему Художники 18 века  Email рассылки в вашем магазине. Советы и примеры использования для решения задач.
Email рассылки в вашем магазине. Советы и примеры использования для решения задач. Оценка соответствия и особенности обращения продукции на территории таможенного союза Е.Петросян
Оценка соответствия и особенности обращения продукции на территории таможенного союза Е.Петросян Возможности электронного документооборота по управлению рисками
Возможности электронного документооборота по управлению рисками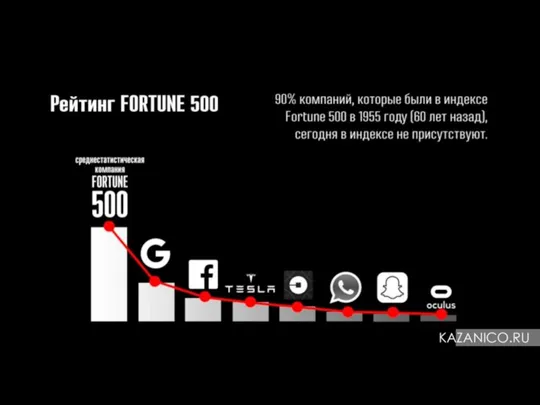 Рейтинг Fortune 5000
Рейтинг Fortune 5000 Закон О предотвращении эмиграции высококачественных z специалистов
Закон О предотвращении эмиграции высококачественных z специалистов Основные вопросы политической сферы
Основные вопросы политической сферы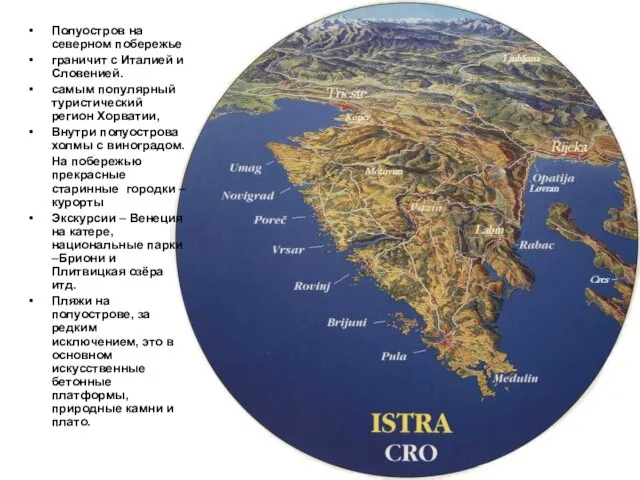 ИСТРА
ИСТРА Расписные военные тарелки Императорского фарфорового завода
Расписные военные тарелки Императорского фарфорового завода Vocabulary. Describing houses and homes
Vocabulary. Describing houses and homes Федеральный государственный образовательный стандарт дошкольного образования от 17.10.2013 № 1155
Федеральный государственный образовательный стандарт дошкольного образования от 17.10.2013 № 1155 Проекты, которые меняют страну к лучшему
Проекты, которые меняют страну к лучшему Загадки Даля
Загадки Даля Биофизика
Биофизика