Содержание
- 2. Свойства многогранников Многогранники представляют собой простейшие тела в пространстве. Многогранные формы мы видим ежедневно: спичичный коробок,
- 3. Исследуем возможность существования правильных многогранников. При этом будем опираться на свойство плоских углов многогранного угла. Теорема:
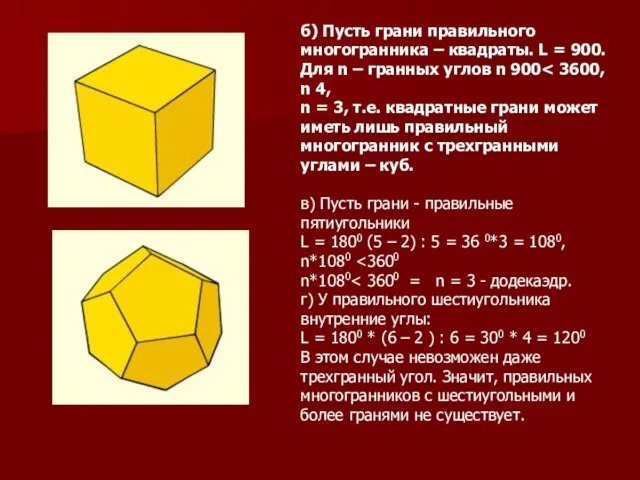
- 4. б) Пусть грани правильного многогранника – квадраты. L = 900. Для n – гранных углов n
- 5. Доказал это соотношение один из величайших математиков Леонард Эйлер (1707 – 1783 гг.), поэтому формула названа
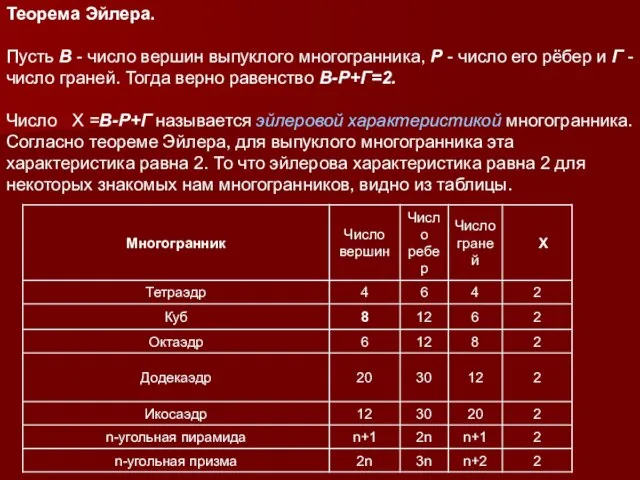
- 6. Теорема Эйлера. Пусть В - число вершин выпуклого многогранника, Р - число его рёбер и Г
- 7. ГЕКСАЭДР(КУБ) Куб составлен из шести квадратов. Каждая его вершина является вершиной трех квадратов. Сумма плоских углов
- 8. ДОДЕКАЭДР Додекаэдр составлен из двенадцати равносторонних пятиугольников. Каждая его вершина является вершиной трех пятиугольников. Сумма плоских
- 9. ТЕТРАЭДР Тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Сумма плоских
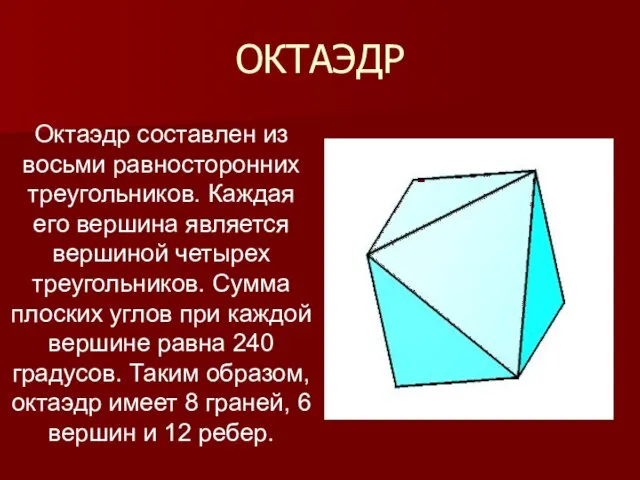
- 10. ОКТАЭДР Октаэдр составлен из восьми равносторонних треугольников. Каждая его вершина является вершиной четырех треугольников. Сумма плоских
- 11. ИКОСАЭДР Икосаэдр составлен из двадцати равносторонних треугольников. Каждая его вершина является вершиной пяти треугольников. Сумма плоских
- 13. Скачать презентацию







 Услуга «Персональный ассистент»
Услуга «Персональный ассистент» Возможные дефекты облицовывания, их предупреждение и устранение
Возможные дефекты облицовывания, их предупреждение и устранение Основы проектной деятельности
Основы проектной деятельности Беспилотная доставка
Беспилотная доставка Картинг, от макета к реальности
Картинг, от макета к реальности Подготовка учащихся к олимпиадам по обществознанию праву, ЕГЭ и ОГЭ
Подготовка учащихся к олимпиадам по обществознанию праву, ЕГЭ и ОГЭ Уважаемые партнеры! Мы рады представить эксклюзивную новинку Color Symphony винил вспененный на флизелине1,06*10m
Уважаемые партнеры! Мы рады представить эксклюзивную новинку Color Symphony винил вспененный на флизелине1,06*10m Очищение и кондиционирование. Предложение для клиента
Очищение и кондиционирование. Предложение для клиента Разработка блок-схем в программе Microsoft Office Visio 2007
Разработка блок-схем в программе Microsoft Office Visio 2007 Вероятность прогноза температур рельсов
Вероятность прогноза температур рельсов Приемная кампания 2012
Приемная кампания 2012 Запрос и предложение - способ коммуникации между заказчиком и исследовательским агентством
Запрос и предложение - способ коммуникации между заказчиком и исследовательским агентством Развитие речи. Заметка. Герои Алтайской земли.
Развитие речи. Заметка. Герои Алтайской земли. Презентация на тему Формирование универсальных учебных действий в образовательном пространстве начальной школы в условиях внедр
Презентация на тему Формирование универсальных учебных действий в образовательном пространстве начальной школы в условиях внедр Презентация по информатике на тему: Поколение третье. Интегральные схемы.
Презентация по информатике на тему: Поколение третье. Интегральные схемы. Цех по изготовлению металлоконструкций п. Балезино. Бизнес-план
Цех по изготовлению металлоконструкций п. Балезино. Бизнес-план Презентация
Презентация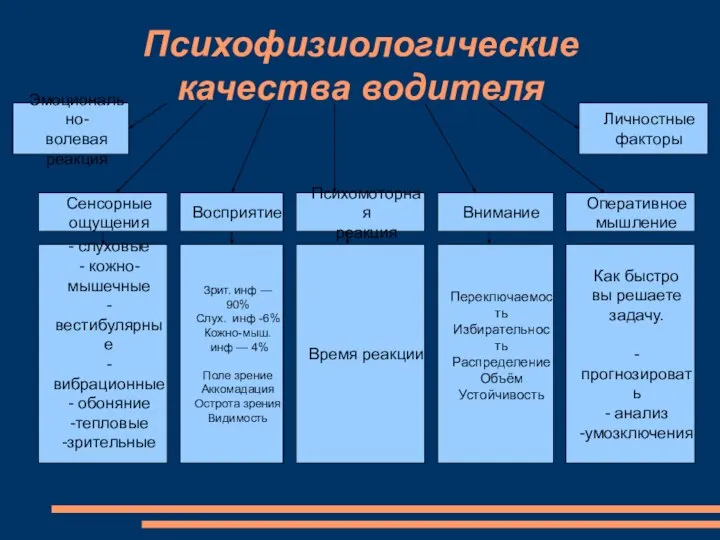 Эмоционально-волевая реакция. Психофизиологические качества водителя
Эмоционально-волевая реакция. Психофизиологические качества водителя Создание изображения для фона презентации
Создание изображения для фона презентации Восстановление славянских государств
Восстановление славянских государств Масла индустриальные ГОСТ 17479.4-87
Масла индустриальные ГОСТ 17479.4-87 Симметрия в живой и неживой природе Выполнили: студенты 1-го курса Факультет: Таможенное дело Группа: Т-116с. Уваров Антон, Панкрат
Симметрия в живой и неживой природе Выполнили: студенты 1-го курса Факультет: Таможенное дело Группа: Т-116с. Уваров Антон, Панкрат МОУ Медведская ООШ ФГОС начальная школа
МОУ Медведская ООШ ФГОС начальная школа Социальные нормы и социальный контроль
Социальные нормы и социальный контроль .
. Презентация
Презентация Самая большая ошибка человека
Самая большая ошибка человека Neizvedannye_zemli
Neizvedannye_zemli