Решение логических задач

Решение логических задач
Внимательно изучить условие.
Выделить простые высказывания и обозначить их латинскими буквами.
Записать условие задачи на языке алгебры логики.
Составить конечную формулу, для этого объединить логическим умножением формулы каждого утверждения, приравнять произведение к единице.
Упростить формулу.
Проанализировать полученный результат или составить таблицу истинности, найти по таблице значения переменных, для которых значение функции равно 1.
Записать ответ

Задача 1
Синоптик объявляет прогноз погоды на завтра и утверждает следующее:
Если не будет ветра, то будет пасмурная погода без дождя.
Если будет дождь, то будет пасмурно и без ветра.
Если будет пасмурная погода, то будет дождь и не будет ветра.
Так какая же погода будет завтра?

1. Выделим простые высказывания и запишем их через переменные: А - «Ветра нет». В - «Будет пасмурная погода». С - «Будет дождь».
2. Запишем логические функции (сложные высказывания):
а) «Если не будет ветра, то будет пасмурная погода без дождя» - А→В ^¬ С.
б) «Если будет дождь, то будет пасмурно и без ветра» - С → В ^ А.
в) «Если будет пасмурная погода, то будет дождь и не будет ветра»- В→С^А.
3. Запишем произведение указанных функций:
F = (А → B ^¬ C) ^ (С → В^ А) ^ (В → С ^А)

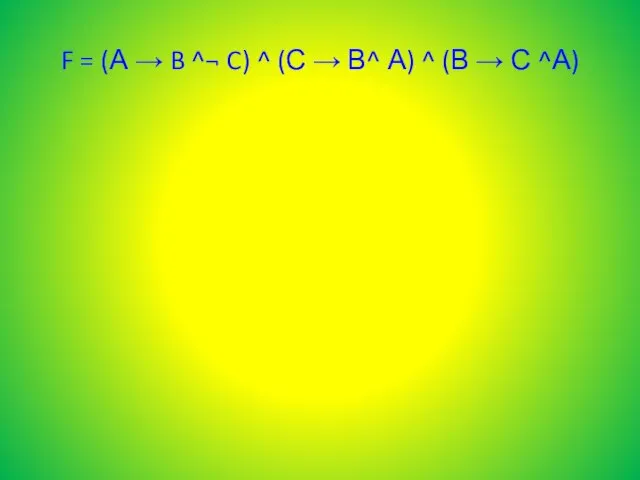
F = (А → B ^¬ C) ^ (С → В^ А) ^ (В → С ^А)

5. Приравняем результат к единице:
А & В & С = 1.
6. Проанализируем результат: логическое произведение равно 1, если каждый множитель равен 1. Поэтому: А = 1, В = 1, С = 1. Значит: А=0, В=0, С=0, то есть ветрено, ясно, без дождя
7. Ответ: погода будет ясная, без дождя, но ветреная.

Домашнее задание
На «3» и «4»
Кто из ребят играет в шахматы, если известно, что:
если играет Андрей или Виктор, то Сергей не играет;
если Виктор не играет, то играют Сергей и Дмитрий;
Сергей играет.

Домашнее задание
На «5»
Маша, Саша и Миша во время летней практики нашли старинную амфору и показали учителю истории. Он попросил высказать каждого их них предположения о том, что это за амфора. Ребята сказали:
Маша: «Эта амфора греческая и изготовлена в V веке».
Саша: «Эта амфора финикийская и изготовлена в III веке».
Миша: «Эта амфора не греческая и изготовлена в IV веке».
Каждый из ребят оказался прав только в одном предположении. Где и в каком веке была изготовлена амфора?

Задача 2
Андреи Маша решили пойти в кино. Каждый из них высказал свои пожелания по поводу выбора фильма.
Андрей сказал: «Я хочу посмотреть французский боевик».
Маша сказала: «Я не хочу смотреть французскую комедию».
Аня сказала: «Я хочу посмотреть американскую мелодраму».
Каждый из них слукавил в одном из двух пожеланий. На какой фильм пошли ребята?

Выделим простые высказывания и запишем их через переменные:
А- «Французский фильм»
В - «Боевик»
С - «Комедия»
¬А- «Американский фильм»
¬В & ¬ С- «мелодрама»

Запишем логические функции (сложные высказывания). Учтем условие о том, что каждый из ребят оказался прав в одном предположении:
а) «Я хочу посмотреть французский боевик» - ¬ А & В v A & ¬ В
б) «Я не хочу смотреть французскую комедию» - ¬ (¬ А & C v A & ¬ C)= ¬ (¬ А&C) & ¬ (A& ¬ C) = (А v ¬ C) & (¬ A v C)
в) «Я хочу посмотреть американскую мелодраму» - ¬ ¬ А & ¬ В &¬ С v ¬ А & ¬ (¬ В & ¬ С) = А & ¬ В &¬ С v ¬ А & ( В v С) = А & ¬ В &¬ С v ¬ А & В v ¬ А & С

(¬ А & В v A & ¬ В) & (А v¬ C) & (¬ A v C) & (А& ¬ В &¬ С v ¬ А & В v ¬ А & С)