Содержание
- 2. Условие задачи В классе 36 человек. После зимних каникул классный руководитель спросил учеников, кто из ребят
- 3. В кино побывало 10 человек; в театре - 14 человек; в цирке - 18 человек; и
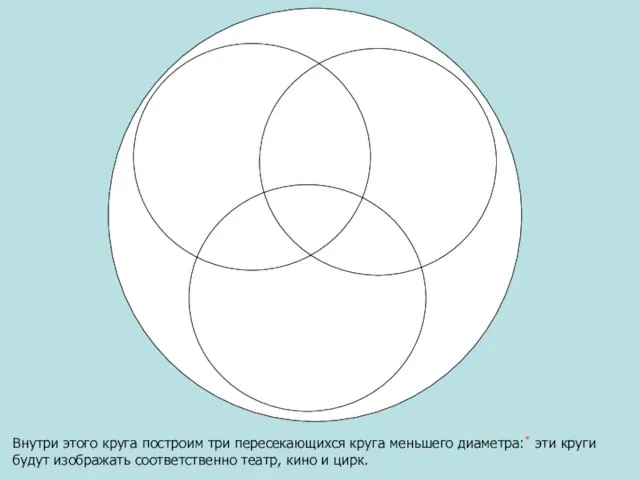
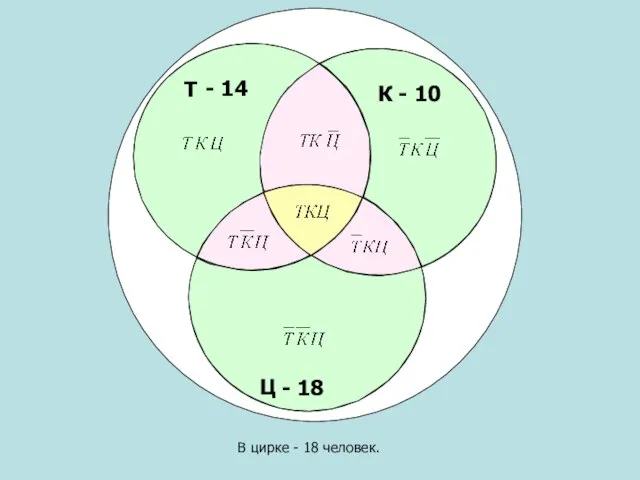
- 4. Пусть большой круг изображает множество всех учеников класса.
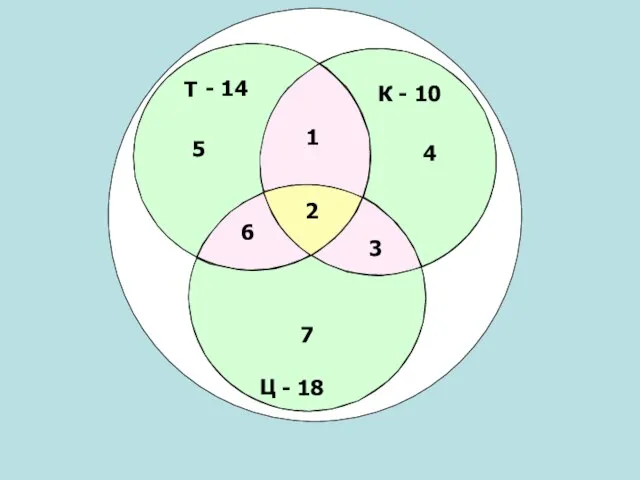
- 5. Внутри этого круга построим три пересекающихся круга меньшего диаметра:* эти круги будут изображать соответственно театр, кино
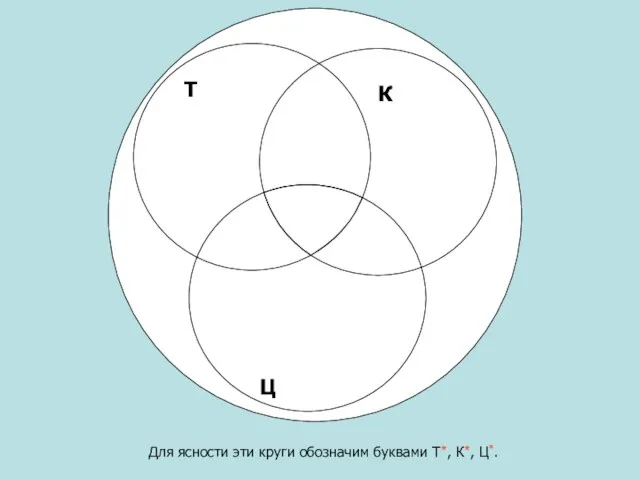
- 6. Для ясности эти круги обозначим буквами Т*, К*, Ц*. Т Т К Ц
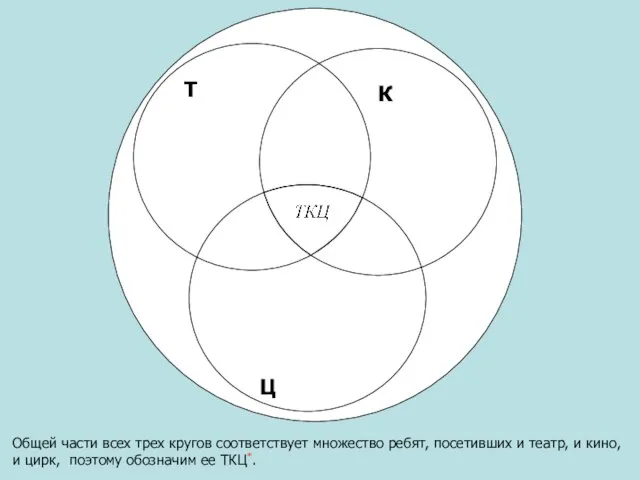
- 7. Общей части всех трех кругов соответствует множество ребят, посетивших и театр, и кино, и цирк, поэтому
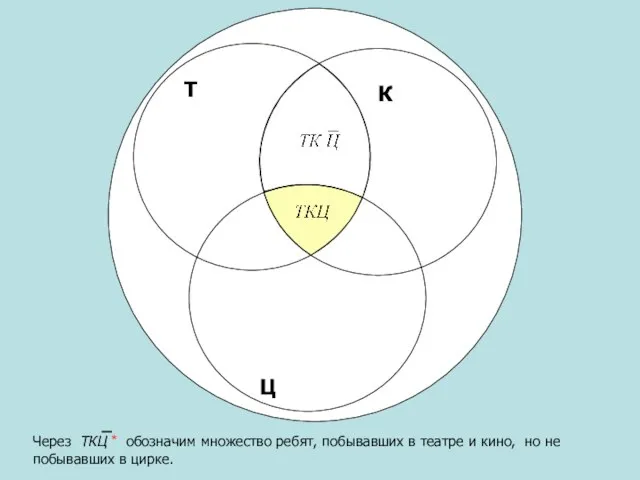
- 8. Через ТКЦ * обозначим множество ребят, побывавших в театре и кино, но не побывавших в цирке.
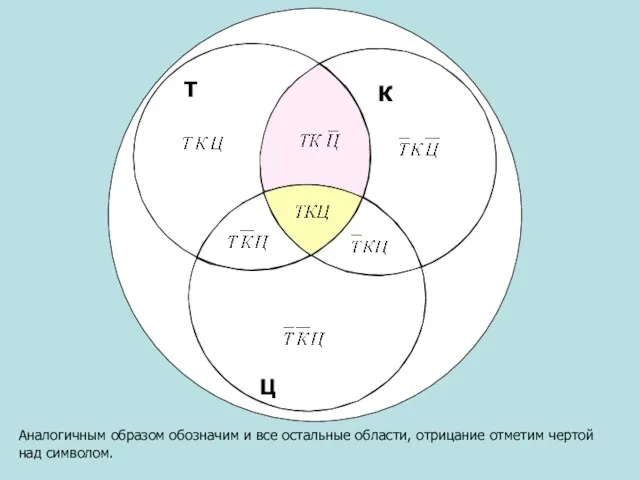
- 9. Аналогичным образом обозначим и все остальные области, отрицание отметим чертой над символом. Т Ц К
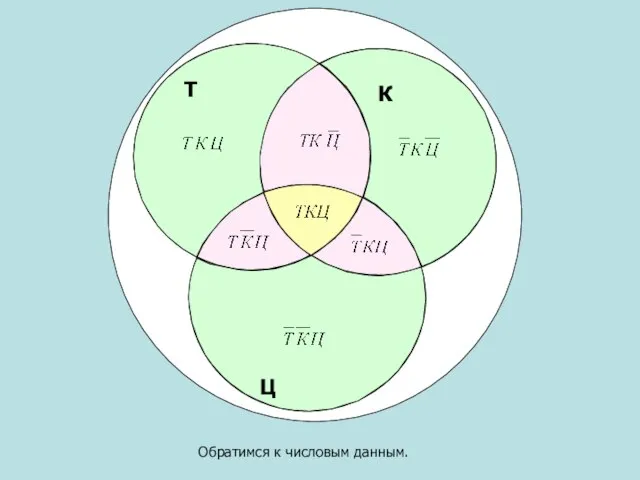
- 10. Обратимся к числовым данным. Т Ц К
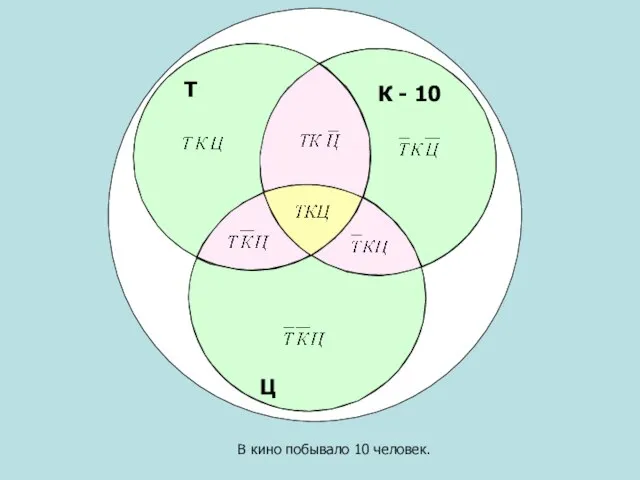
- 11. В кино побывало 10 человек. Т Ц К - 10
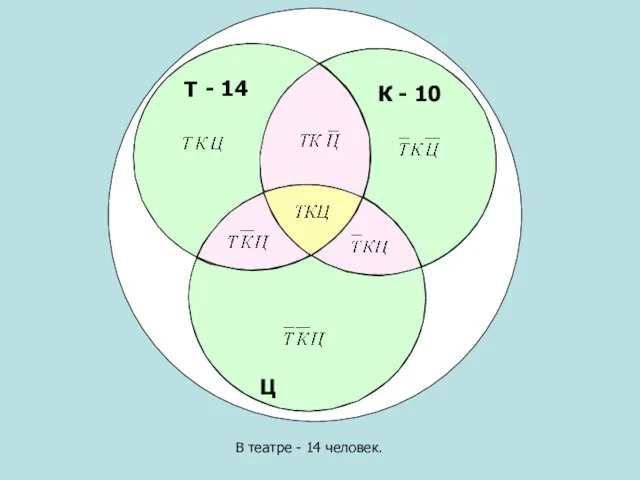
- 12. Т К - 10 - 14 В театре - 14 человек. Ц
- 13. Т К - 10 - 14 В цирке - 18 человек. Ц - 18
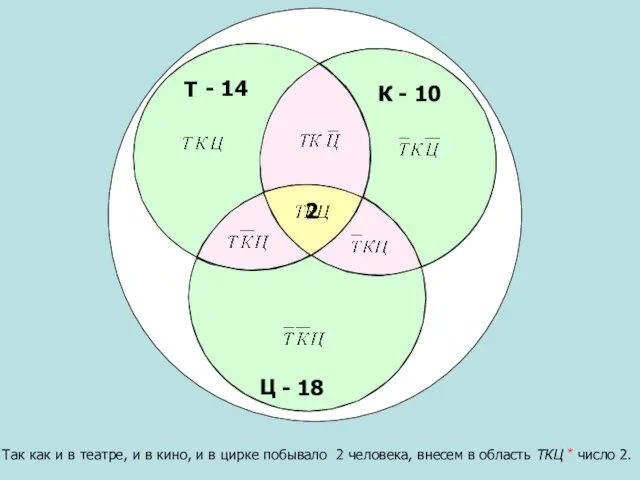
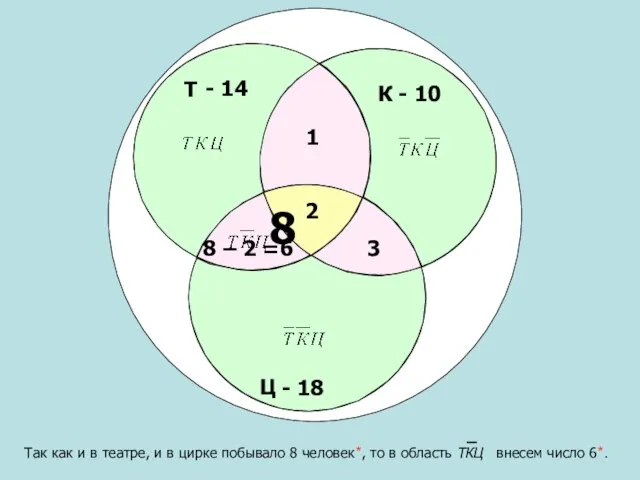
- 14. Т Ц К - 10 - 14 Так как и в театре, и в кино, и
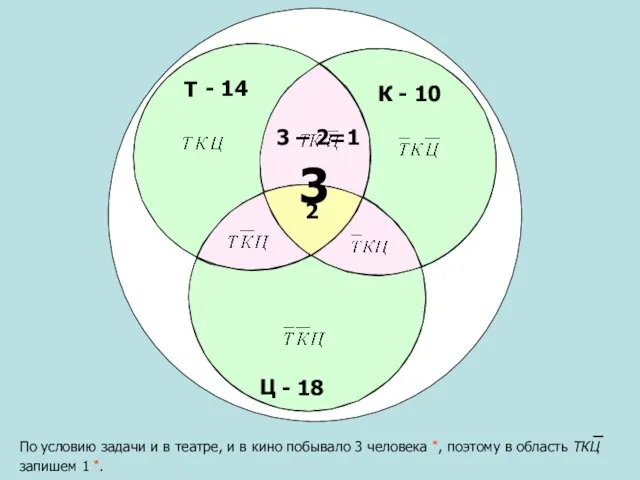
- 15. Т Ц К - 10 - 14 По условию задачи и в театре, и в кино
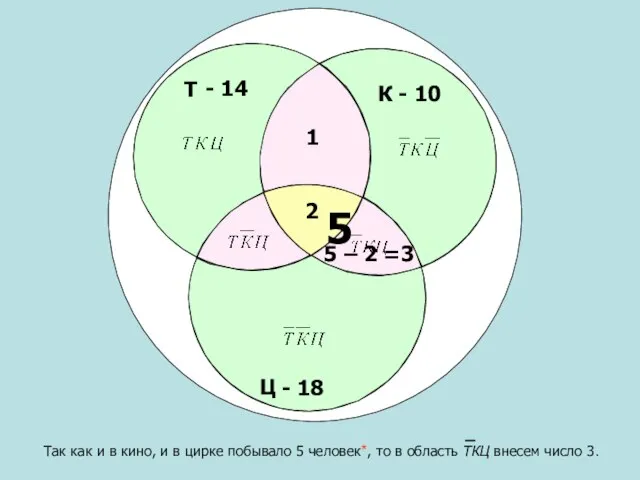
- 16. Т Ц К - 10 - 14 Так как и в кино, и в цирке побывало
- 17. Т Ц К - 10 - 14 Так как и в театре, и в цирке побывало
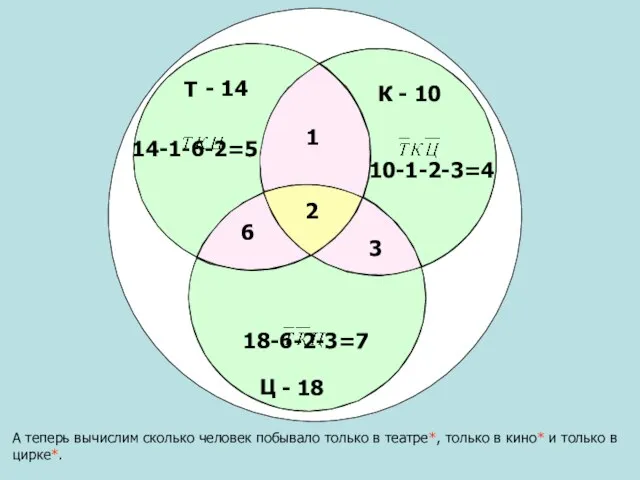
- 18. Т Ц К - 10 - 14 А теперь вычислим сколько человек побывало только в театре*,
- 19. Т Ц К - 10 - 14 - 18 2 3 1 6 5 4 7
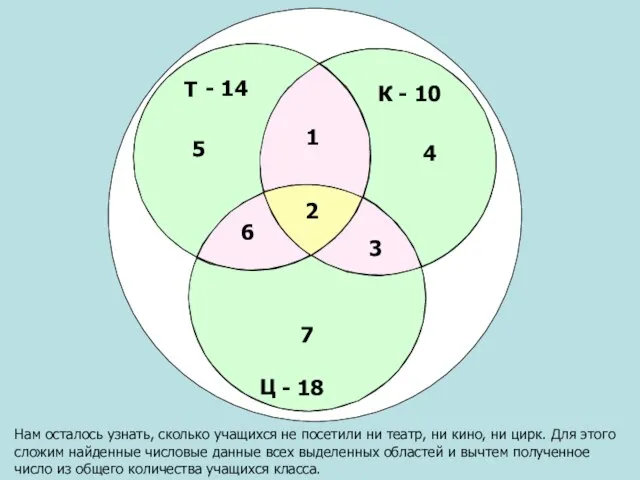
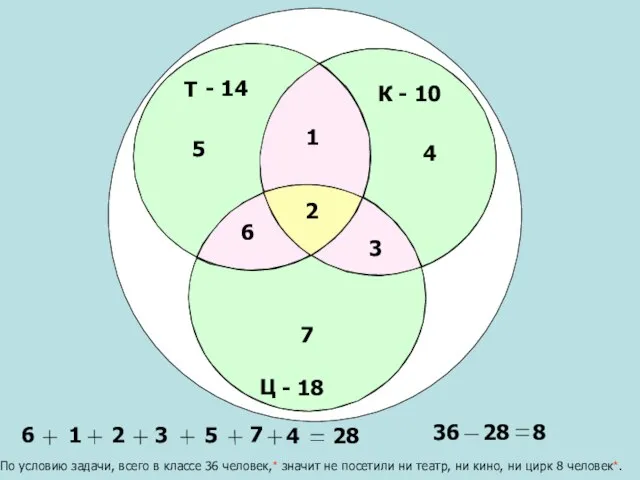
- 20. Нам осталось узнать, сколько учащихся не посетили ни театр, ни кино, ни цирк. Для этого сложим
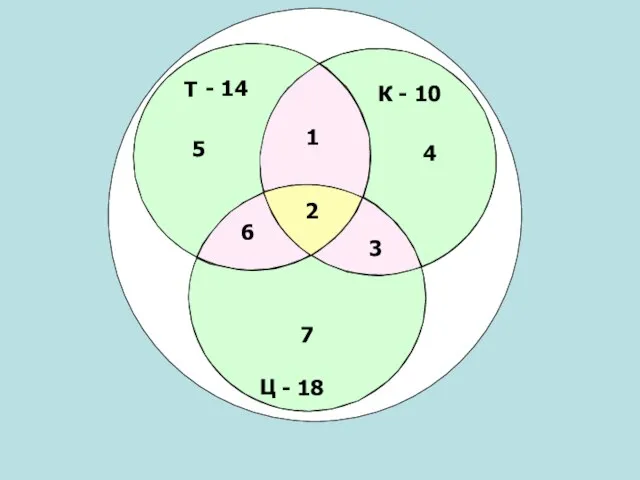
- 21. Т Ц К - 10 - 14 - 18 2 3 1 6 5 4 7
- 22. Т Ц К - 10 - 14 - 18 2 3 1 6 5 4 7
- 24. Скачать презентацию



 701661
701661 Только в боге мы находим силу побеждать (фотографии)
Только в боге мы находим силу побеждать (фотографии) Имена собственные (1 класс)
Имена собственные (1 класс) "Площади и объемы"
"Площади и объемы" Проектирование участка механической обработки по изготовлению детали Вал-шестерня одноступенчатого цилиндрического редуктора
Проектирование участка механической обработки по изготовлению детали Вал-шестерня одноступенчатого цилиндрического редуктора Мы показываем кукол, а куклы показывают нам мир.
Мы показываем кукол, а куклы показывают нам мир. Тайны жизни растений
Тайны жизни растений Российско-французский форум «Государственно-частное партнерство в развитии региональной и муниципальной инфраструктуры»Модел
Российско-французский форум «Государственно-частное партнерство в развитии региональной и муниципальной инфраструктуры»Модел Рождество в США
Рождество в США ЯЗЫК БЛОК - СХЕМ
ЯЗЫК БЛОК - СХЕМ Курская битва
Курская битва Шаблон презентации
Шаблон презентации Усовершенствование сайта библиотеки и веб-интерфейса электронного каталога библиотеки вуза как путь навстречу пользователю
Усовершенствование сайта библиотеки и веб-интерфейса электронного каталога библиотеки вуза как путь навстречу пользователю Добро пожаловать в Третьяковскую галерею
Добро пожаловать в Третьяковскую галерею Фестиваль ледоколов 2019
Фестиваль ледоколов 2019 Привитие навыков здорового образа жизни у школьников
Привитие навыков здорового образа жизни у школьников Признание самовольной постройки законной
Признание самовольной постройки законной Правовые основы охраны труда
Правовые основы охраны труда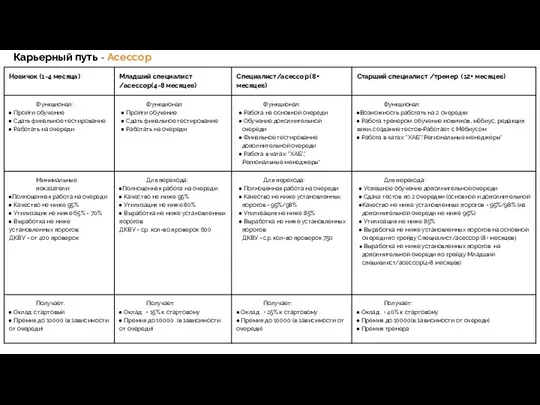 Карьерный путь - Асессор Новичок (1-4 месяца)
Карьерный путь - Асессор Новичок (1-4 месяца) МОУ «Репяховская ООШ»
МОУ «Репяховская ООШ» БРЕЙН - РИНГ
БРЕЙН - РИНГ Присоединение Бурятии к России. 17 век.
Присоединение Бурятии к России. 17 век. Прыжки в высоту. Упражнения с набивными мячами. 5 класс
Прыжки в высоту. Упражнения с набивными мячами. 5 класс Архитектурные памятники Дзержинщины
Архитектурные памятники Дзержинщины Основы Конституционного строя РФ
Основы Конституционного строя РФ Договор возмездного оказания услуг Подготовил студент 4 курса ФТД, ДС-04, Шарипов Ш.Д.
Договор возмездного оказания услуг Подготовил студент 4 курса ФТД, ДС-04, Шарипов Ш.Д. Имате вебсајт и што да правите со него?
Имате вебсајт и што да правите со него?