Решение уравнений, содержащих знак абсолютной величины

Гипотеза исследования
Если мы будем знать способы решения уравнений, содержащих знак абсолютной величины, будем уметь их классифицировать на группы, то это позволит нам без особых усилий решать уравнения такого типа.

Цель исследования: изучить различные способы решения уравнений, содержащих знак абсолютной величины.
Задачи исследования:
Познакомиться с понятием модуля, его свойствами, графиком;
Рассмотреть различные способы решения уравнений, содержащих модуль;
Составить памятку-практикум для обучающихся 8-9 классов.

Уравнения, содержащие знак абсолютной величины в курсе математики 5-8 классов.
Различные способы решения уравнений, содержащих знак модуля.
Объект исследования:
Предмет исследования:

Методы исследования
1) теоретические: изучение и анализ научно-теоретической литературы по теме работы;
2) эмпирические: провести анализ различных способов решения уравнений, содержащих знак модуля.

История возникновения модуля
Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера». Считают, что термин предложил использовать английский математик Котс, ученик Ньютона. Общепринятое обозначение абсолютной величины (модуля) введено в 1841 году Вейерштрассом.

Определение модуля
Абсолютной величиной (модулем) действительного числа a называется само число a, если a - неотрицательное число, и число противоположное a, если a - отрицательное число.

Основные свойства модуля:
1)
3)
4)
2)
5)
6)

Пример: решить уравнение
нули подмодульных выражений – это числа - 4 и 3.
2)
МЕТОД ИНТЕРВАЛОВ

а) Если x < - 4 , то данное уравнение примет вид: - (x + 4) – (x – 3) = 7,
- x – 4 – x + 3 =7,
- 2 x = 8,
x = - 4,
- 4 не удовлетворяет условию x < - 4, значит при
x < - 4 данное уравнение не имеет корней.
МЕТОД ИНТЕРВАЛОВ

б) Если – 4 ≤ x ≤ 3, то данное уравнение примет вид:
( x + 4) – (x – 3) = 7,
x + 4 – x + 3 = 7,
7 = 7,
верно для любого значения х из взятого промежутка. Значит данное уравнение верно для всех х, удовлетворяющих условию – 4 ≤ x ≤ 3.
МЕТОД ИНТЕРВАЛОВ

в) Если х > 3, то данное уравнение примет вид:
(х + 4) + (х – 3) = 7,
2 х + 1 = 7,
2 х = 6,
х = 3,
3 не удовлетворяет условию х > 3, значит, при
x > 3 данное уравнение не имеет корней.
Ответ. - 4 ≤ х ≤ 3.
МЕТОД ИНТЕРВАЛОВ

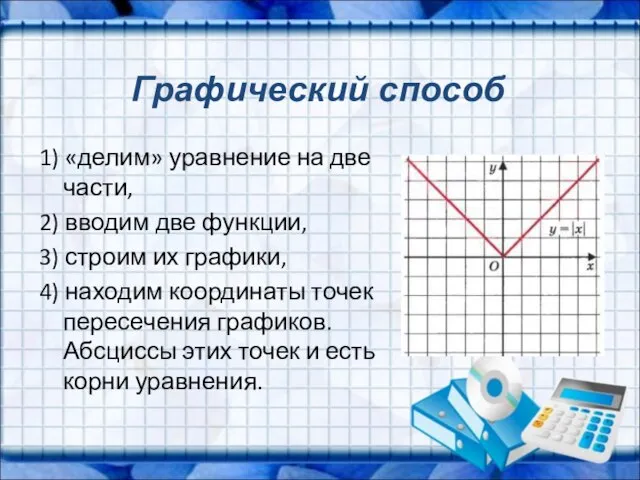
Графический способ
1) «делим» уравнение на две части,
2) вводим две функции,
3) строим их графики,
4) находим координаты точек пересечения графиков. Абсциссы этих точек и есть корни уравнения.

Решить уравнение
Решение: Решим уравнение графически, представив его в виде
Строим два графика
и
Графики функций пересекаются в точке x=2.
Ответ. 2.
Графический способ

Практическая часть исследования
памятка-практикум для обучающихся 8-9 классов;
тесты;
упражнения и задания различной трудности;
ответы ко всем типам заданий.

Заключение
познакомились с понятием модуля, его свойствами, геометрической интерпретацией;
обобщили понятие абсолютной величины;
рассмотрели свойства модуля;
по результатам исследования составлен методический материал;
гипотеза исследования была подтверждена;