Решение уравнений

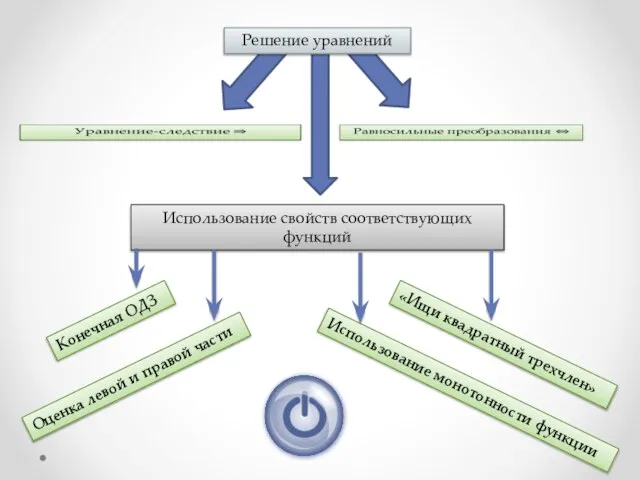
Использование свойств соответствующих функций
Решение уравнений
Конечная ОДЗ
Оценка левой и правой части
Использование монотонности функции
«Ищи квадратный трехчлен»

Уравнение-следствие
При использовании уравнений-следствий проверка подстановкой в исходное уравнение является составной частью решения.
Для получения уравнения-следствия достаточно посмотреть на заданное уравнение как на верное числовое равенство и гарантировать, что каждое следующее уравнение мы можем получить как верное числовое равенство
Пример:

Посмотрим на данное уравнение как на верное числовое равенство. А именно: если в верном числовом равенстве перенести член из одной части в другую с противоположным знаком, то равенство не нарушится.
Если числа равны то и квадраты равны.
Если оби части верного неравенства разделить на число 2≠0, то равенство не нарушится.
Раскрывая скобки и перенося все члены в одну сторону, мы снова получаем верное равенство, откуда находим корни неполного квадратного уравнения
Проверка:
При х=0
получаем неверное равенство (-1=1)
При х=3
получаем верное равенство (1=1)
Поскольку для решения уравнения мы использовали уравнение-следствие, то в решение входит также проверка найденных корней подстановкой в исходное уравнение
Ответ: 3
Если числа равны то и квадраты равны.

СХЕМА ВЫПОЛНЕНИЯ РАВНОСИЛЬНЫХ ПРЕОБРАЗОВАНИЙ УРАВНЕНИЙ
Учесть ОДЗ исходного уравнения
Гарантировать (на ОДЗ) прямые и обратные преобразования
Пример:

Ответ: 3.
= 2
> 0,
> 0,
≠ 1,

Конечная ОДЗ
Если область допустимых значений (ОДЗ) уравнения (или системы) состоит из конечного числа значений, то для решения достаточно проверить все эти значения
У некоторых уравнений область определения состоит только из конечного числа
точек. Для решения таких уравнений достаточно проверить, не являются ли найденные числа из области определения уравнения корнями этого уравнения.
Пример:

Ответ: 1.

Оценка левой и правой части уравнения
Сумма нескольких неотрицательных функций равна нулю тогда и только тогда, когда все функции одновременно равны нулю.
Пример:
Пример:

Ответ: х=0

Решение:
Ответ: х=2
Сумма нескольких неотрицательных функций равна нулю тогда и только тогда, когда все функции одновременно равны нулю.

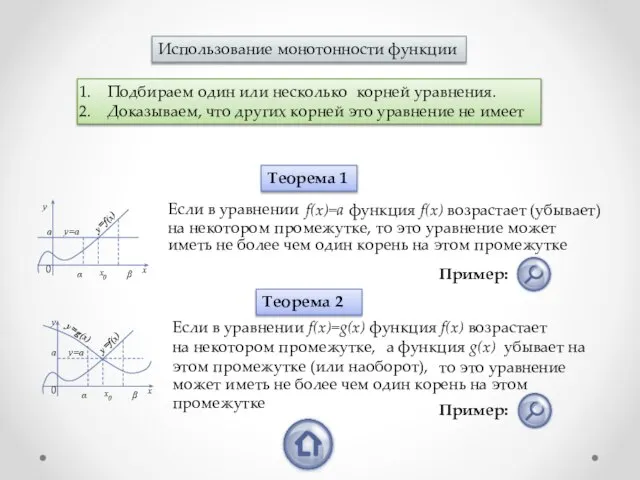
Использование монотонности функции
Подбираем один или несколько корней уравнения.
Доказываем, что других корней это уравнение не имеет
x
α
β
x0
a
y=a
y=f(x)
0
x
α
β
x0
a
y=a
y=f(x)
0
y=g(x)
Если в уравнении
f(x)=a
функция f(x) возрастает (убывает)
на некотором промежутке,
то это уравнение может
иметь не более чем один корень на этом промежутке
y
Теорема 1
y
Теорема 2
Если в уравнении f(x)=g(x) функция f(x) возрастает
на некотором промежутке,
а функция g(x) убывает на
то это уравнение
этом промежутке (или наоборот),
может иметь не более чем один корень на этом
промежутке
Пример:
Пример:

1. Подбираем один или несколько корней уравнения.
2. Доказываем, что других корней это уравнение не имеет
Ответ: х=1.

1. Подбираем один или несколько корней уравнения.
2. Доказываем, что других корней это уравнение не имеет
Ответ: х=2

«Ищи квадратный трёхчлен»
Попробуйте рассмотреть данное уравнение как квадратное
относительно какой-либо переменной
(или какой-либо функции)
Решение:

Используемая литература
Е.П.Нелин Алгебра в таблицах 7-11, «Определения, свойства, методы решения задач в таблицах»;
Е.П.Нелин Методы решения алгебраических задач (приложение к учебному пособию «Алгебра в таблицах»)