Решение задач лп в excel

Общая задача линейного программирования решается симплексным методом
Симплекс (лат. simplex - простой) – простейший выпуклый многогранник
в n-мерном пространстве с n+1 вершиной (например, тетраэдр в 3-мерном пространстве)

Если задача линейного программирования имеет оптимальное решение, то оно соответствует хотя бы одной угловой точке многогранника решений (и совпадает с одним из допустимых базисных решений системы ограничений)
На рисунке: оптимальное решение находится в одной из вершин многоугольника решений А, В, С, D

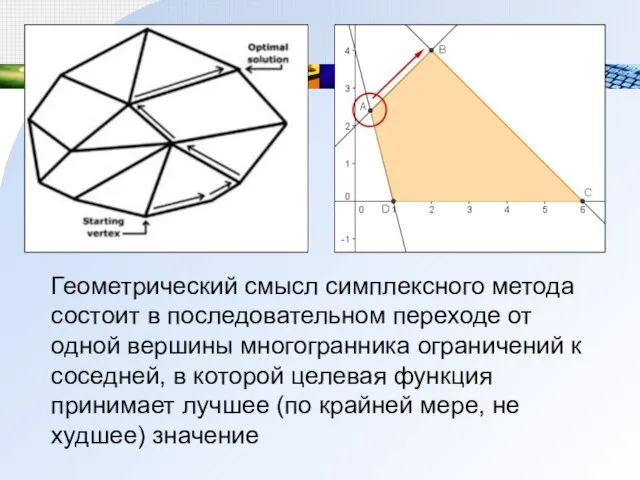
Геометрический смысл симплексного метода состоит в последовательном переходе от одной вершины многогранника ограничений к соседней, в которой целевая функция принимает лучшее (по крайней мере, не худшее) значение

Впервые симплексный метод был предложен американским ученым Дж. Данцигом в 1949 г.
Джордж Бернард Данциг (1914-2005) – американский математик, разработал симплексный алгоритм, считается основоположником методов линейного программирования
Леонид Витальевич Канторович (1912-1986) – советский математик и экономист, лауреат Нобелевской премии по экономике 1975 года «за вклад в теорию оптимального распределения ресурсов». Один из создателей линейного программирования
Идеи симплексного метода были разработаны в 1939 г. российским ученым Л.В.Канторовичем

Симплексный метод позволяет решить любую задачу линейного программирования
В настоящее время он используется для компьютерных расчетов
Рассмотрим решение задачи линейного программирования в MS Excel

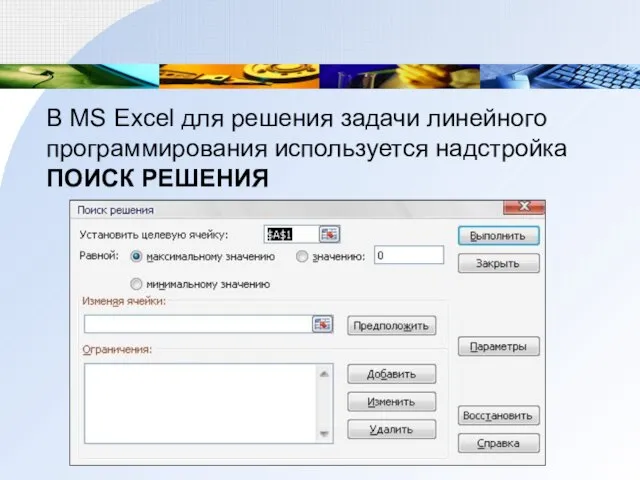
В MS Excel для решения задачи линейного программирования используется надстройка ПОИСК РЕШЕНИЯ

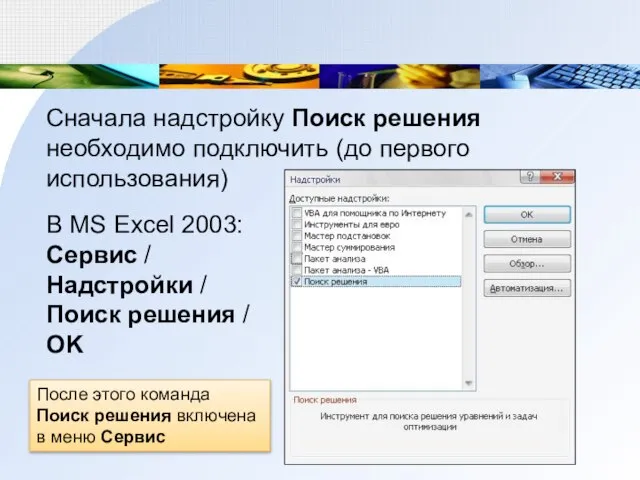
Сначала надстройку Поиск решения необходимо подключить (до первого использования)
В MS Excel 2003: Сервис /
Надстройки /
Поиск решения /
OK
После этого команда Поиск решения включена в меню Сервис

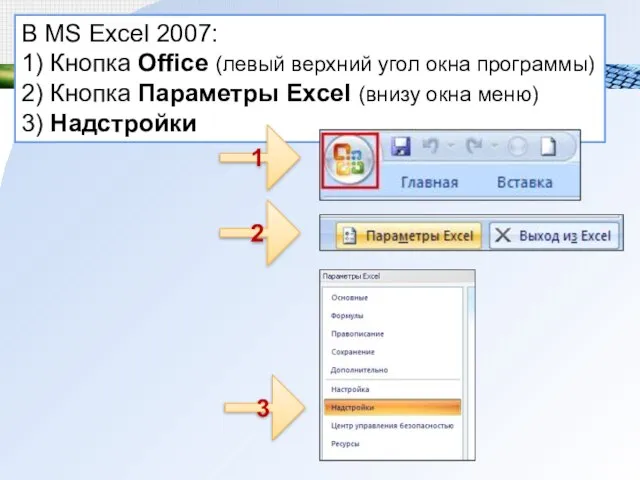
В MS Excel 2007:
1) Кнопка Office (левый верхний угол окна программы)
2) Кнопка Параметры Excel (внизу окна меню)
3) Надстройки
1
2
3

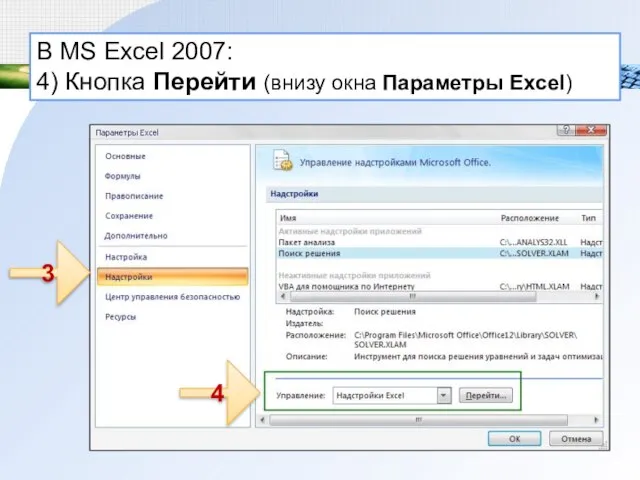
В MS Excel 2007:
4) Кнопка Перейти (внизу окна Параметры Excel)
4
3

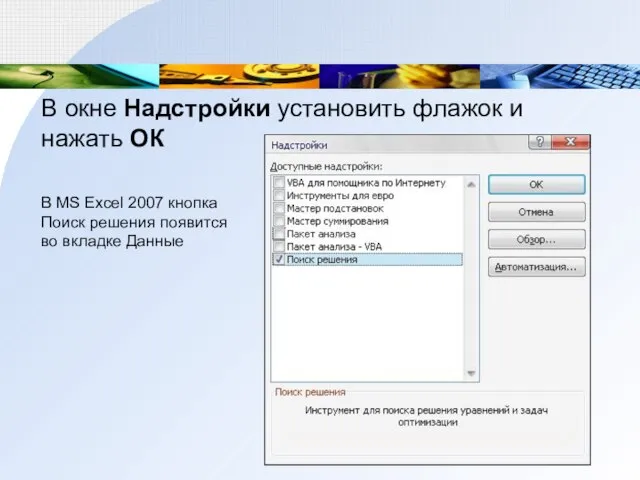
В окне Надстройки установить флажок и нажать ОК
В MS Excel 2007 кнопка Поиск решения появится во вкладке Данные

В MS Excel 2007 кнопка Поиск решения появится во вкладке Данные

Решим в MS Excel задачу линейного программирования
1
2

Решим в MS Excel задачу линейного программирования
3
4
СРС
СРС

Ответы:
1
2
3
4

Решим в MS Excel задачу линейного программирования
1. Создадим область переменных
Ячейки В2:В6 будут играть роль переменных
(пока они пусты)

Решим в MS Excel задачу линейного программирования
2. Введем формулу вычисления значений целевой функции
Например, в ячейку А8

Решим в MS Excel задачу линейного программирования
3. Создадим область ограничений
В ячейках А11:А13 будем вычислять левые части ограничений в системе
В ячейках В11:В13 введем правые части ограничений системы

Решим в MS Excel задачу линейного программирования
3. Создадим область ограничений
В ячейках А11:А13 будем вычислять левые части ограничений в системе
Первое ограничение

Решим в MS Excel задачу линейного программирования
3. Создадим область ограничений
В ячейках А11:А13 будем вычислять левые части ограничений в системе
Второе ограничение

Решим в MS Excel задачу линейного программирования
3. Создадим область ограничений
В ячейках А11:А13 будем вычислять левые части ограничений в системе
Третье ограничение

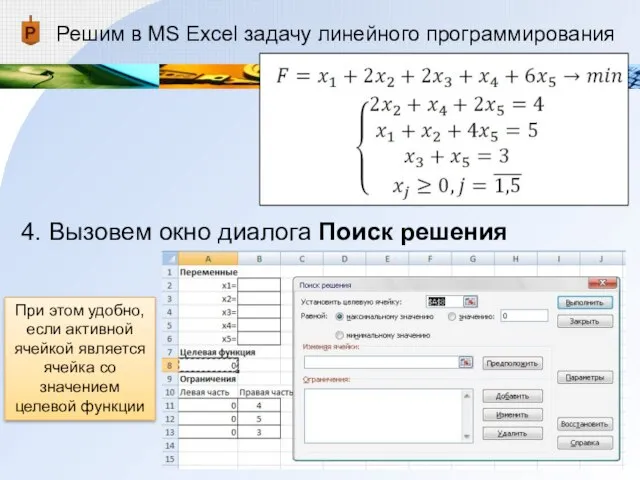
Решим в MS Excel задачу линейного программирования
4. Вызовем окно диалога Поиск решения
При этом удобно, если активной ячейкой является ячейка со значением целевой функции

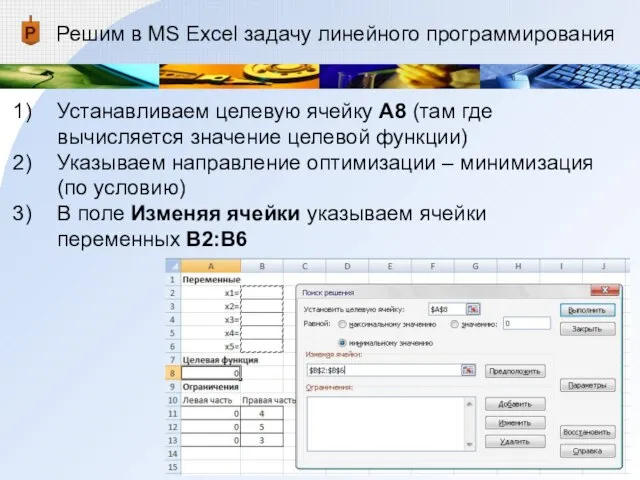
Решим в MS Excel задачу линейного программирования
Устанавливаем целевую ячейку А8 (там где вычисляется значение целевой функции)
Указываем направление оптимизации – минимизация (по условию)
В поле Изменяя ячейки указываем ячейки переменных В2:В6

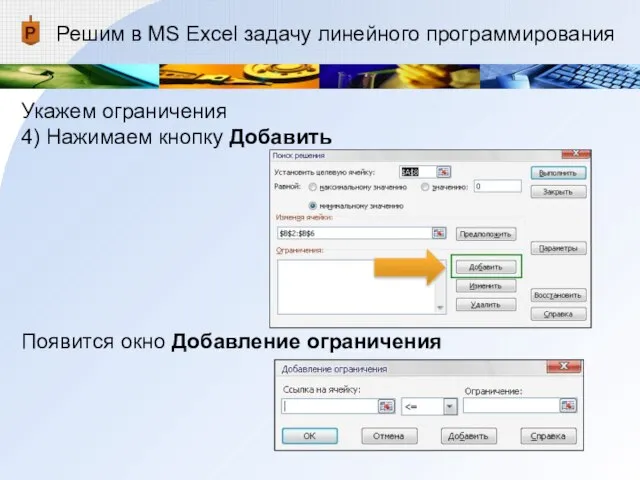
Решим в MS Excel задачу линейного программирования
Укажем ограничения
4) Нажимаем кнопку Добавить
Появится окно Добавление ограничения

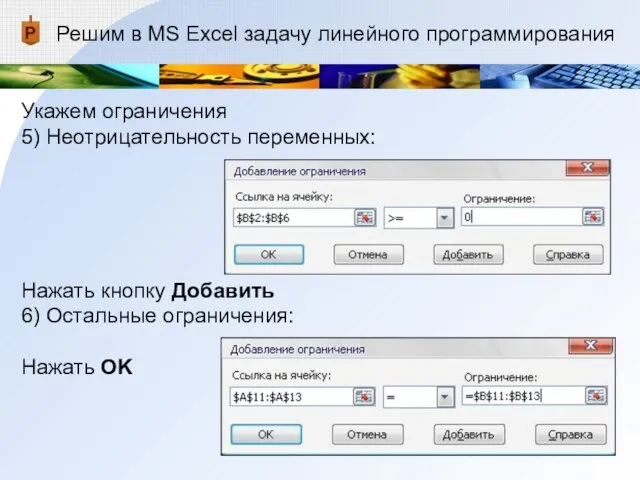
Решим в MS Excel задачу линейного программирования
Укажем ограничения
5) Неотрицательность переменных:
Нажать кнопку Добавить
6) Остальные ограничения:
Нажать OK

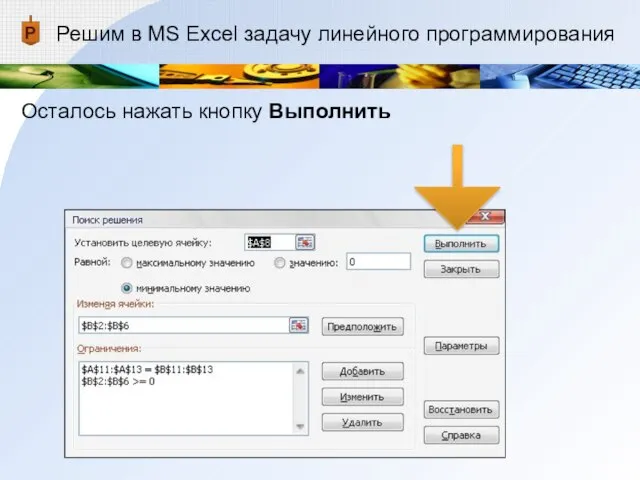
Решим в MS Excel задачу линейного программирования
Осталось нажать кнопку Выполнить

Решим в MS Excel задачу линейного программирования
Результаты
Ответ: