Содержание
- 2. 1%−это сотая часть рассматриваемой величины (52% от х кг − это 0,52х кг); Если в смеси
- 3. вода кислота вода вода кислота кислота 600 г 15% 10% 30% Х г 600−Х г 0,3Х
- 4. медь олово медь олово олово 15+Х кг 70% 60% 15 кг Х кг 0,6∙15 кг 0,7(15+Х)
- 5. алюминий магний алюминий магний магний 22+Х+15=37+Х кг Х+15 кг Х кг 22+Х кг 100∙(Х+15)/(37+Х) % +
- 6. Смесь, состоящая из двух веществ, весит 18 кг. После того, как из нее выделили 40 %
- 7. медь цинк медь медь цинк 2Х+40 кг 2Х−60 кг 100 кг х−60 кг 0,7(2Х+40) кг +
- 8. Для приготовления лекарства потребовался 76 %-ный спирт. Провизор налил в колбу 220 г 95 %-ного спирта.
- 10. Скачать презентацию
Слайд 21%−это сотая часть рассматриваемой величины (52% от х кг − это 0,52х
1%−это сотая часть рассматриваемой величины (52% от х кг − это 0,52х

Если в смеси растворов объемом V (массой m) нас интересует компонент объемом V0 (массой m0), то процентное содержание этого вещества можно просчитать по формуле:
P0=(V0/V)∙100% или P0=(m0/m) ∙100% ;
В качестве неизвестных обычно выбирают объемы или массы компонентов смеси (сплава);
Складывать, уравнивать, сравнивать можно только массовые доли одного и того же вещества, или веществ в смеси (сплаве).
При решении таких задач важно знать, что:
Слайд 3вода
кислота
вода
вода
кислота
кислота
600 г
15%
10%
30%
Х г
600−Х г
0,3Х г
0,1(600−Х) г
0,15∙600 г
+
=
0,3Х+0,1(600−Х)=0,15∙600, Х=150
150 г первого раствора, тогда
вода
кислота
вода
вода
кислота
кислота
600 г
15%
10%
30%
Х г
600−Х г
0,3Х г
0,1(600−Х) г
0,15∙600 г
+
=
0,3Х+0,1(600−Х)=0,15∙600, Х=150
150 г первого раствора, тогда
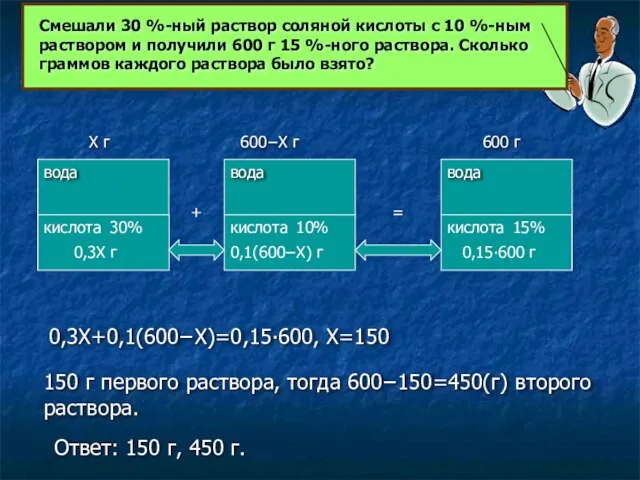
Ответ: 150 г, 450 г.
Смешали 30 %-ный раствор соляной кислоты с 10 %-ным раствором и получили 600 г 15 %-ного раствора. Сколько граммов каждого раствора было взято?
Слайд 4медь
олово
медь
олово
олово
15+Х кг
70%
60%
15 кг
Х кг
0,6∙15 кг
0,7(15+Х) кг
+
=
0,6∙15+Х=0,7(15+Х), Х=5.
5 кг олова надо добавить, чтобы
медь
олово
медь
олово
олово
15+Х кг
70%
60%
15 кг
Х кг
0,6∙15 кг
0,7(15+Х) кг
+
=
0,6∙15+Х=0,7(15+Х), Х=5.
5 кг олова надо добавить, чтобы

Ответ: 5 кг.
Имеется кусок сплава меди с оловом массой 15 кг, содержащий 40% меди. Сколько чистого олова надо прибавить к этому куску, чтобы получившийся новый сплав содержал 30 % меди?
40%
30%
Слайд 5алюминий
магний
алюминий
магний
магний
22+Х+15=37+Х кг
Х+15 кг
Х кг
22+Х кг
100∙(Х+15)/(37+Х) %
+
=
100Х/(22+Х)+33=100(Х+15)/(37+Х), Х=3.
Таким образом, сплав первоначально весил 25
алюминий
магний
алюминий
магний
магний
22+Х+15=37+Х кг
Х+15 кг
Х кг
22+Х кг
100∙(Х+15)/(37+Х) %
+
=
100Х/(22+Х)+33=100(Х+15)/(37+Х), Х=3.
Таким образом, сплав первоначально весил 25
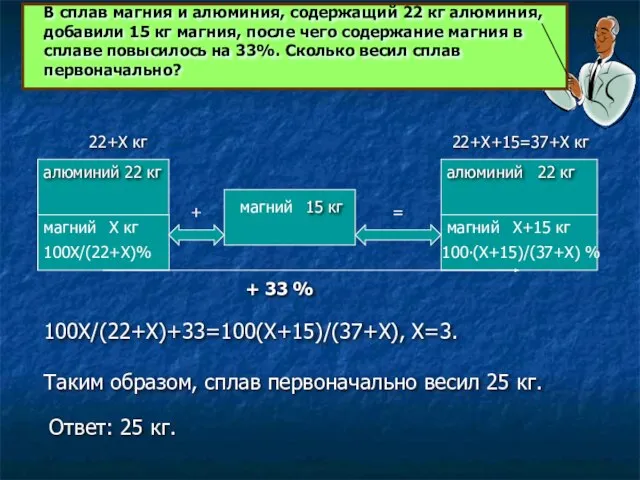
Ответ: 25 кг.
В сплав магния и алюминия, содержащий 22 кг алюминия, добавили 15 кг магния, после чего содержание магния в сплаве повысилось на 33%. Сколько весил сплав первоначально?
22 кг
15 кг
100Х/(22+Х)%
+ 33 %
22 кг
Слайд 6Смесь, состоящая из двух веществ, весит 18 кг. После того, как из
Смесь, состоящая из двух веществ, весит 18 кг. После того, как из

1 вещество
2 вещество
40 %
25 %
18 кг
60 %
75 %
Х кг
У кг
0,6Х кг
0,75У кг
+
=
=
Х+У=18,
0,6Х=0,75У.
Х=10,
У=8.
1-го вещества было 10 кг, а 2-го вещества было 8 кг.
Ответ: 10 кг, 8 кг.
Слайд 7медь
цинк
медь
медь
цинк
2Х+40 кг
2Х−60 кг
100 кг
х−60 кг
0,7(2Х+40) кг
+
=
Х+100=0,7(2Х+40), Х=180.
180 кг было меди в первоначальном
медь
цинк
медь
медь
цинк
2Х+40 кг
2Х−60 кг
100 кг
х−60 кг
0,7(2Х+40) кг
+
=
Х+100=0,7(2Х+40), Х=180.
180 кг было меди в первоначальном

Ответ: 60 %.
Латунь − сплав меди и цинка. Кусок латуни содержит меди на 60 кг больше, чем у цинка. Этот кусок латуни сплавили со 100 кг меди и получили латунь, в которой 70 % меди. Определите процент содержания меди в первоначальном куске латуни.
?%
70%
Х кг
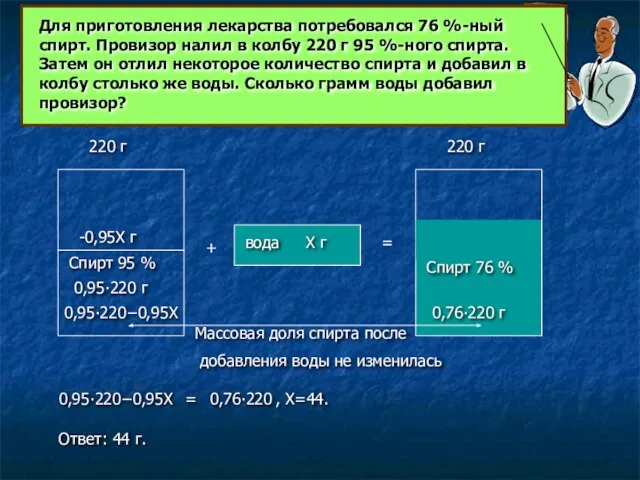
Слайд 8Для приготовления лекарства потребовался 76 %-ный спирт. Провизор налил в колбу 220
Для приготовления лекарства потребовался 76 %-ный спирт. Провизор налил в колбу 220
220 г
Спирт 95 %
+
=
220 г
Спирт 76 %
вода
0,95∙220 г
-0,95Х г
Х г
0,95∙220−0,95Х
0,76∙220 г
Массовая доля спирта после
добавления воды не изменилась
0,95∙220−0,95Х
=
0,76∙220
, Х=44.
Ответ: 44 г.
 Пермский край: инвестиционные возможности
Пермский край: инвестиционные возможности Системные платы Gigabyte
Системные платы Gigabyte Кроссворд на английском языке
Кроссворд на английском языке Проектирование системы электроснабжения электроаппаратного завода
Проектирование системы электроснабжения электроаппаратного завода Древние образы народного искусства
Древние образы народного искусства Решение квадратных уравнений
Решение квадратных уравнений Антимонопольное регулирование в авторитейле
Антимонопольное регулирование в авторитейле Завтрак чемпиона от Широковой Полины. Омлет с сыром, молоко
Завтрак чемпиона от Широковой Полины. Омлет с сыром, молоко Highlights of sports
Highlights of sports Просвещенный абсолютизм в России
Просвещенный абсолютизм в России Феофан Грек, Андрей Рублев
Феофан Грек, Андрей Рублев "Платон" - Философия
"Платон" - Философия Народы и государства восточного полушария в начале VI в.
Народы и государства восточного полушария в начале VI в. Деятельность
Деятельность ЖИЗНЬ КЛАССА 1 сентября Посвящение в гимназисты Хореография Экскурсия в Автогородок Новогодний калейдоскоп Масленица Наша пл
ЖИЗНЬ КЛАССА 1 сентября Посвящение в гимназисты Хореография Экскурсия в Автогородок Новогодний калейдоскоп Масленица Наша пл ОРГАНИЗАЦИЯ ПЕРЕВОЗКИ ВНЕШНЕТОРГОВЫХ ГРУЗОВ АВТОМОБИЛЬНЫМ ТРАНСПОРТОМ Преподаватель: доцент кафедры МЭО, к.э.н., Журова А.В.
ОРГАНИЗАЦИЯ ПЕРЕВОЗКИ ВНЕШНЕТОРГОВЫХ ГРУЗОВ АВТОМОБИЛЬНЫМ ТРАНСПОРТОМ Преподаватель: доцент кафедры МЭО, к.э.н., Журова А.В. Участники "Первого Дома на Родине" отмечают свою первую Хануку в Израиле
Участники "Первого Дома на Родине" отмечают свою первую Хануку в Израиле Реклама и маркетинг
Реклама и маркетинг Изображение цветка пиона в разных техниках художественной обработки
Изображение цветка пиона в разных техниках художественной обработки Мутационная изменчивость 10 класс
Мутационная изменчивость 10 класс Byredo Blanche. Парфюмерия
Byredo Blanche. Парфюмерия Элетромеханический замок с убегающим кодом
Элетромеханический замок с убегающим кодом Особенности формирования требований информационной безопасности Реестра источников ионизирующего излучения (ИИИ), которые могут
Особенности формирования требований информационной безопасности Реестра источников ионизирующего излучения (ИИИ), которые могут Valentine game
Valentine game Аспартам
Аспартам Попечительский совет или Управляющий совет?
Попечительский совет или Управляющий совет? Компания Декорсталь – Производитель декоративных сталей
Компания Декорсталь – Производитель декоративных сталей Taller de comunicación oral y escrita
Taller de comunicación oral y escrita