Режимы с обострением и коэволюция систем

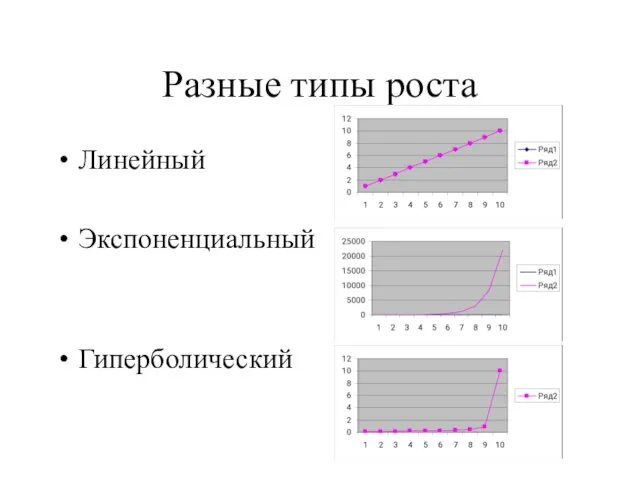
Разные типы роста
Линейный
Экспоненциальный
Гиперболический

Примеры обратимого развития, застоя, колебательных систем и т.п.
Авиация, космонавтика, многие фирмы и многое другое

Экспоненциальный рост- колония бактерий

Гиперболический рост
Положительная обратная связь
Уход величин на бесконечность за конечное время (режим с обострением)
Принцип Чернавского
Нелинейность
Единство системы

Видовое разнообразие

Гиперболический рост процессов в обществе
население
информация
ВВП
H. Foerster, P. Mora, L. Amiot,
1960.Doomsday, Friday, 13
November A.D. 2026, Science, 132; 1291-5.

Российские исследователи
Труды И.М. Дьяконова, Л.Е. Гринина, А.Д. Панова, А.П. Назаретяна, С.П. Капицы, А.В. Коротаева, А.С. Малкова, Д.А. Халтуриной и др.

Логистическое уравнение

История человечества
Первый пример перехода гиперболического роста в логистическую кривую – осевое время

Современная ситуация
Демографический взрыв и проблема перенаселения.
Демографический вопрос в русском космизме.
Изменения происходят на масштабе жизни одного человека.

ВВП на душу населения- на встречу экономике изобилия.
Когда ожидать наличие бесконечного числа товаров и услуг у каждого гражданина земли?

Коэволюция
В системе, где 2 взаимодействующие подсистемы развиваются по определенному закону имеет место понятие коэволюции. Коэволюция предполагает гармоническое совместное развитие систем. Если этот принцип нарушается, то в системе может возникнуть дисбаланс, приводящий к ее разрушению.

. Коэволюция двух систем с гиперболическим ростом и линейным перераспределением ресурса.

Системы с единым моментом обострения
Angus Maddison “The world economy: a millennial perspective”.

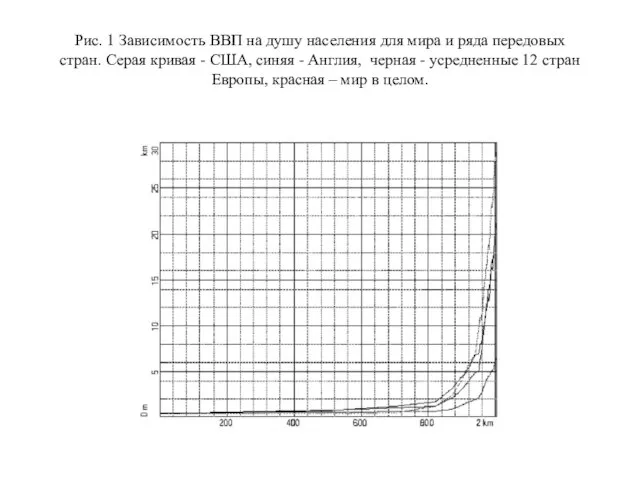
Рис. 1 Зависимость ВВП на душу населения для мира и ряда передовых стран. Серая кривая - США, синяя - Англия, черная - усредненные 12 стран Европы, красная – мир в целом.

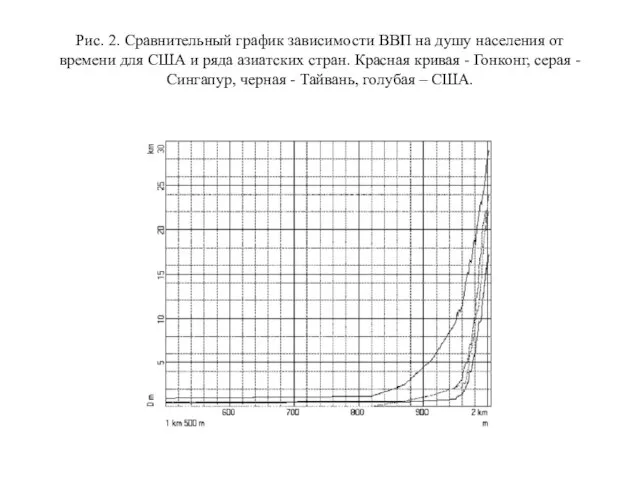
Рис. 2. Сравнительный график зависимости ВВП на душу населения от времени для США и ряда азиатских стран. Красная кривая - Гонконг, серая - Сингапур, черная - Тайвань, голубая – США.

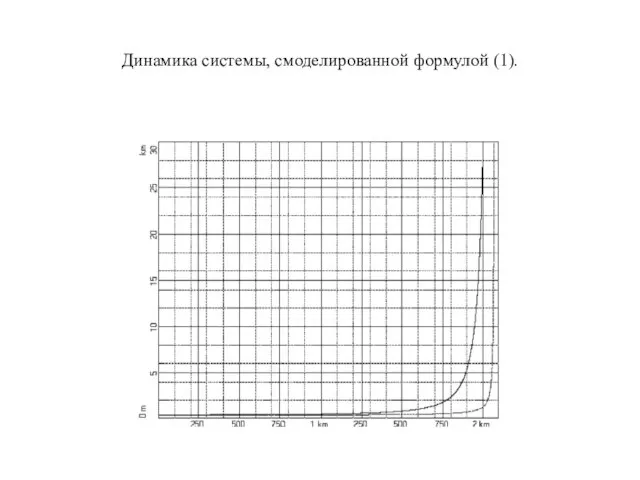
Динамика системы, смоделированной формулой (1).