Сечение ударной электронной ионизации. Оже-электроны

Лекция 9 Слайд 2
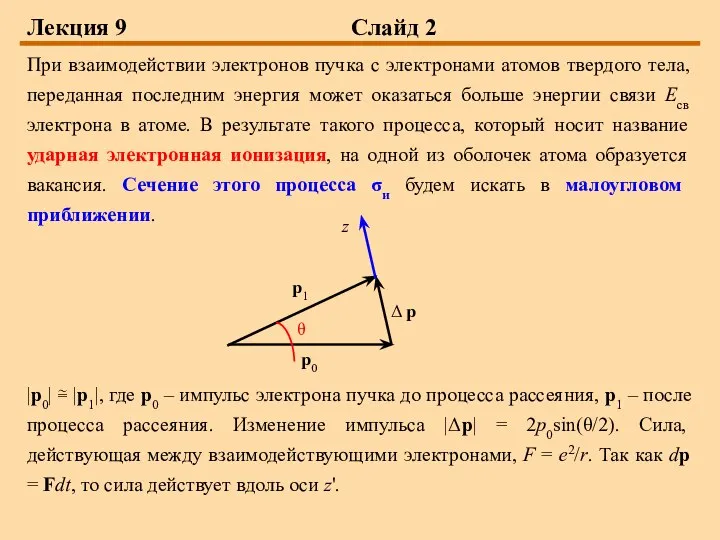
При взаимодействии электронов пучка с электронами атомов твердого тела, переданная последним энергия может оказаться больше энергии связи Есв электрона в атоме. В результате такого процесса, который носит название ударная электронная ионизация, на одной из оболочек атома образуется вакансия. Сечение этого процесса σи будем искать в малоугловом приближении.
|р0| ≅ |р1|, где р0 – импульс электрона пучка до процесса рассеяния, р1 – после процесса рассеяния. Изменение импульса |Δр| = 2р0sin(θ/2). Сила, действующая между взаимодействующими электронами, F = e2/r. Так как dp = Fdt, то сила действует вдоль оси z'.

Лекция 9 Слайд 3
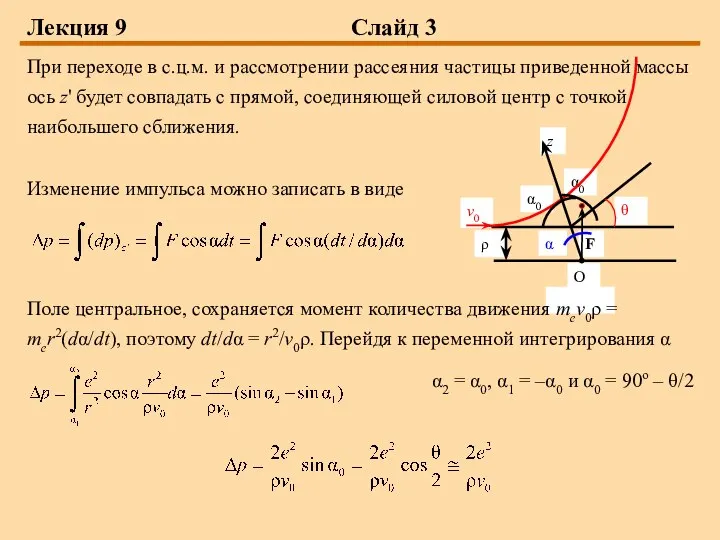
При переходе в с.ц.м. и рассмотрении рассеяния частицы приведенной массы ось z' будет совпадать с прямой, соединяющей силовой центр с точкой наибольшего сближения.
Изменение импульса можно записать в виде
Поле центральное, сохраняется момент количества движения mev0ρ = mer2(dα/dt), поэтому dt/dα = r2/v0ρ. Перейдя к переменной интегрирования α
α2 = α0, α1 = –α0 и α0 = 90о – θ/2

Лекция 9 Слайд 4
Энергия, переданная атомному электрону
Е0 – энергия электрона пучка перед процессом взаимодействия с атомным электроном.
Следовательно ρ2 = (е4/Е0)/Т 2ρdρ = –(е4/Е0)(dТ/Т2).
Дифференциальное сечение ударной электронной ионизации
Чтобы получить σи необходимо проинтегрировать по всем возможным переданным энергиям от Tmin = Eсв до Tmax = E0.

Лекция 9 Слайд 5
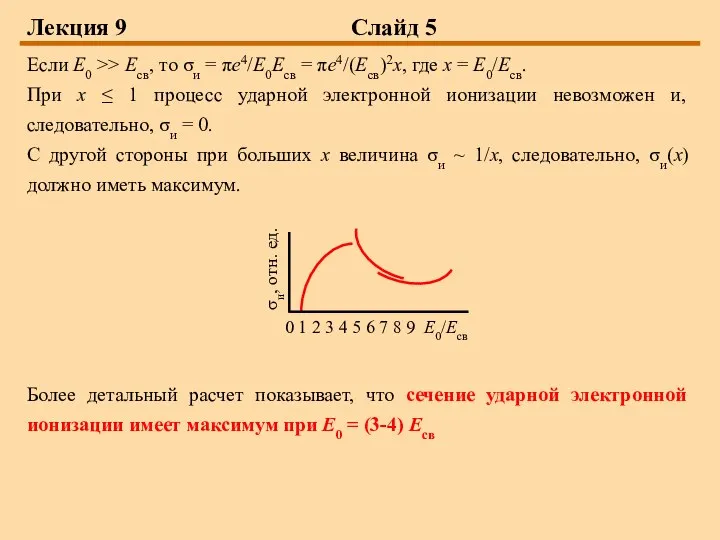
Если E0 >> Eсв, то σи = πе4/E0Eсв = πе4/(Eсв)2х, где х = E0/Eсв.
При х ≤ 1 процесс ударной электронной ионизации невозможен и, следовательно, σи = 0.
С другой стороны при больших х величина σи ~ 1/х, следовательно, σи(х) должно иметь максимум.
Более детальный расчет показывает, что сечение ударной электронной ионизации имеет максимум при E0 = (3-4) Eсв

Лекция 9 Слайд 6
Для описания состояния отдельного электрона в атоме необходимо задать четыре квантовых числа:
главное квантовое число n = 1, 2, 3, …7 – определяет основное значение энергии электрона в атоме, которое в первом приближении есть –13,6Z 2/n2 эВ;
орбитальное квантовое число l при заданном n может принимать значения 0, 1, 2, …, n – 1, определяет угловой орбитальный момент электрона;
квантовое число углового момента j при заданном l может принимать значения ⏐l ± 1⏐, характеризует полный угловой момент электрона, складывающийся из орбитального углового момента и спина;
магнитное квантовое число mj при заданном j может принимать все полуцелые значения от - j до + j , определяет проекцию полного углового момента электрона на заданное направление.

Лекция 9 Слайд 7
Электроны, занимающие в атоме энергетические уровни с одинаковым главным квантовым числом n, образуют оболочку. Максимальное число электронов в оболочке 2n2, так как в соответствии с принципом Паули в каждом состоянии может находиться один электрон. Электронные оболочки с различными значениями n обозначают заглавными латинскими буквами следующим образом:
Состояния с различными значениями l имеют следующие спектроскопические обозначения:
Число состояний с одинаковыми n, l и j равно 2j + 1.
Совокупность электронов с такими квантовыми числами - подоболочка, на которой может быть до 2j +1 электронов, различающихся значениями mj.

Лекция 9 Слайд 8
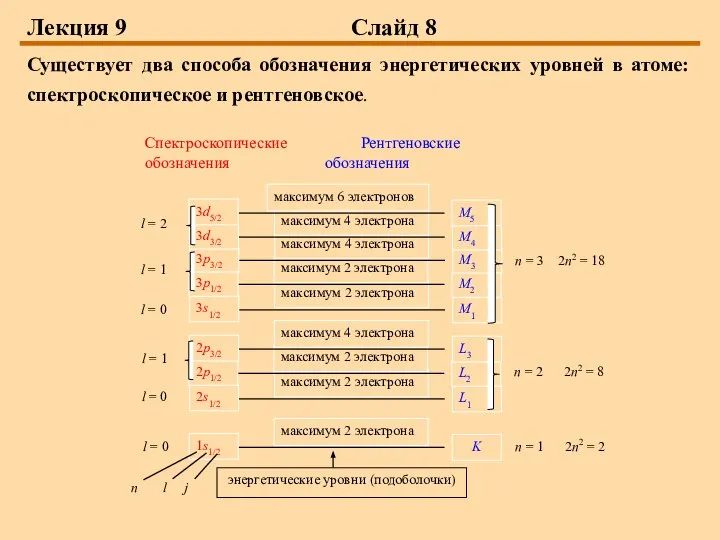
Существует два способа обозначения энергетических уровней в атоме: спектроскопическое и рентгеновское.

Лекция 9 Слайд 9
Оже-процесс
испущенный атомом электрон – Оже-электрон
Данный переход обозначается KL1L1
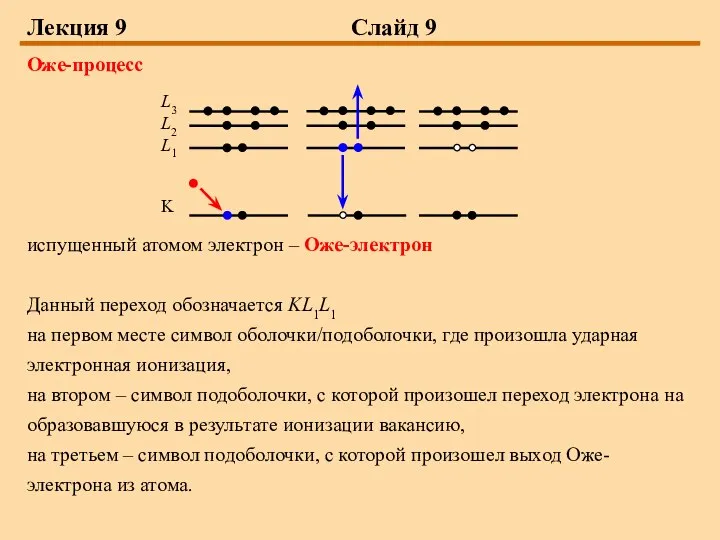
на первом месте символ оболочки/подоболочки, где произошла ударная электронная ионизация,
на втором – символ подоболочки, с которой произошел переход электрона на образовавшуюся в результате ионизации вакансию,
на третьем – символ подоболочки, с которой произошел выход Оже-электрона из атома.

Лекция 9 Слайд 10
Полное обозначение Оже-перехода включает также конечное состояние атома в спектроскопических обозначениях. Рассмотренный переход оставляет пустой оболочку 2s и полностью заполненными оболочки 2р, поэтому полное обозначение данного перехода KL1L1 (2s02р6).
При ионизации К-оболочки возможны также переходы KL1L2,3 с конечным состоянием (2s12р5), KL2L2,3 и KL3L3с конечным состоянием (2s22р4), т.е. всего 6 переходов. Наибольшую интенсивность имеет переход KL2L3.
Если ударная электронная ионизация произошла на L-оболочке, то вакансию заполняет электрон с М-оболочки, а другому электрону М-оболочки передается избыток энергии и он выходит из атома. Обозначения подобных переходов LММ.

Лекция 9 Слайд 11
Переходы Костера-Кронига
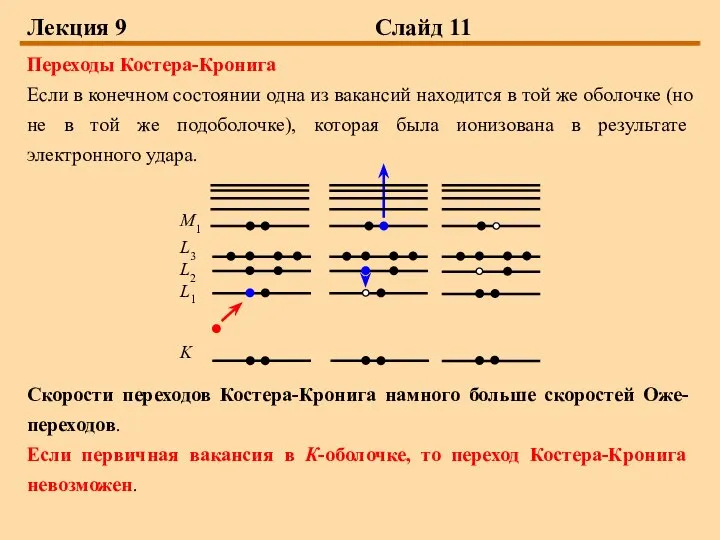
Если в конечном состоянии одна из вакансий находится в той же оболочке (но не в той же подоболочке), которая была ионизована в результате электронного удара.
Скорости переходов Костера-Кронига намного больше скоростей Оже-переходов.
Если первичная вакансия в К-оболочке, то переход Костера-Кронига невозможен.

Лекция 9 Слайд 12
Энергия Оже-электрона в первом приближении может быть вычислена исходя из энергий связи электронов, участвующих в Оже-процессе. В частности, для перехода KL2L3
Это выражение не учитывает наличие вакансий, которое немного изменяет энергии связи. Точные значения ЕА приведены в справочниках.
Так как энергии связи разные для разных элементов, то, определив энергию Оже-электрона, можно сказать, каким элементом испущен данный электрон. На этом основан метод Оже-электронной спектроскопии, который будет подробно рассмотрен в следующем семестре.

Лекция 9 Слайд 13
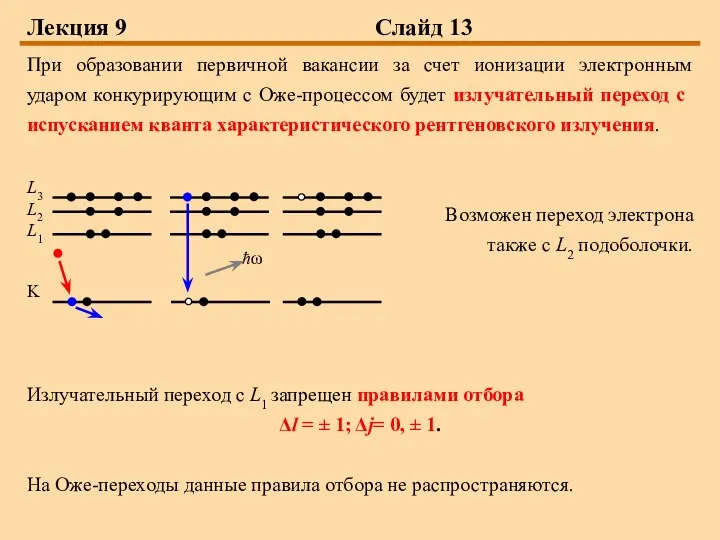
При образовании первичной вакансии за счет ионизации электронным ударом конкурирующим с Оже-процессом будет излучательный переход с испусканием кванта характеристического рентгеновского излучения.
Возможен переход электрона
также с L2 подоболочки.
Излучательный переход с L1 запрещен правилами отбора
Δl = ± 1; Δj= 0, ± 1.
На Оже-переходы данные правила отбора не распространяются.

Лекция 9 Слайд 14
Схема излучательного перехода при заполнении вакансии с подоболочки L3
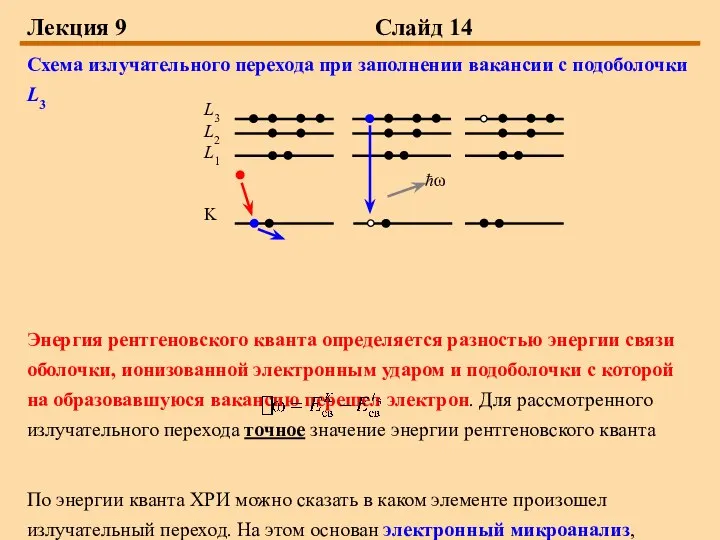
Энергия рентгеновского кванта определяется разностью энергии связи оболочки, ионизованной электронным ударом и подоболочки с которой на образовавшуюся вакансию перешел электрон. Для рассмотренного излучательного перехода точное значение энергии рентгеновского кванта
По энергии кванта ХРИ можно сказать в каком элементе произошел излучательный переход. На этом основан электронный микроанализ, который будет подробно рассмотрен в следующем семестре.

Лекция 9 Слайд 15
Система обозначений для излучательных переходов (линии ХРИ)
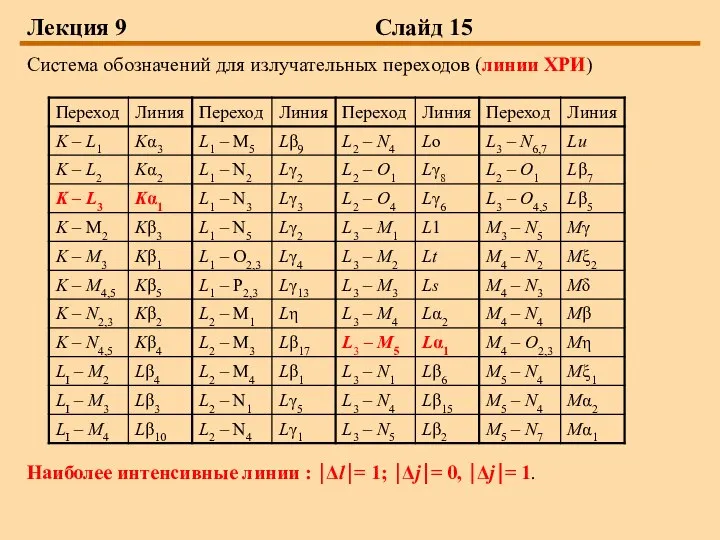
Наиболее интенсивные линии : ⏐Δl⏐= 1; ⏐Δj⏐= 0, ⏐Δj⏐= 1.