Содержание
- 2. Симметрия СИММЕТРИЯ, в геометрии — свойство геометрических фигур. Две точки, лежащие на одном перпендикуляре к данной
- 3. Основные понятия теории симметрии Какие тела обычно считают равными? Такие, которые при взаимном наложении совмещаются друг
- 4. Двусторонняя симметрия Под отражениями понимают любые зеркальные отражения — в точке, линии, плоскости. Воображаемая плоскость, которая
- 5. Нульмерная симметрия Нульмерная симметрия, присуща телам, бесконечно вытянутым ни в одном особенном направлении. Очевидно, такова симметрия
- 6. Одномерная симметрия Одномерная симметрия присуща телам, во-первых, вытянутым в одном каком-либо особенном направлении, во-вторых, вытянутым в
- 7. Двумерная симметрия Двумерной симметрией обладают тела, во-первых, вытянутые в двух взаимно перпендикулярных направлениях, во-вторых, вытянутые в
- 8. Трехмерная симметрия Трехмерная симметрия присуща телам, во-первых, вытянутым в трех взаимно перпендикулярных направлениях, во-вторых, вытянутым в
- 9. Дисимметрические объекты Объекты, симметрия которых исчерпывается лишь простыми (круговыми), или (и) переносными (трансляционными), или (и) винтовыми
- 10. Формы дисимметрических объектов Дисимметрические объекты могут существовать в двух разновидностях: в виде оригинала и зеркального отражения
- 11. Биологическая изомерия Самое главное достижение — создание теории строения П- и Л-биообъектов. На ее основе было
- 12. Частота встреч П- и Л-формы биообъектов. Как часто встречаются П- и Л-формы биообъектов? Найдено, что частота
- 13. Свойства П- и Л-форм. Основное достижение — это открытие дисимметрии жизни (СССР). Оказывается, ряд свойств П-
- 14. Причина свойств П- и Л-форм Никакой теории, отвечающей на этот вопрос, пока не существует. Предложенные гипотезы
- 15. Интересный факт Много интересных фактов может сообщить наука о симметрии и о человеке. Как известно, в
- 16. Заключение Конечно, смена видов симметрии по мере эволюции жизни происходила не только у дисимметрических организмов. Так,
- 18. Скачать презентацию
Слайд 2Симметрия
СИММЕТРИЯ, в геометрии — свойство геометрических фигур. Две точки, лежащие на
Симметрия
СИММЕТРИЯ, в геометрии — свойство геометрических фигур. Две точки, лежащие на

Слайд 3Основные понятия теории симметрии
Какие тела обычно считают равными? Такие, которые при взаимном
Основные понятия теории симметрии
Какие тела обычно считают равными? Такие, которые при взаимном

Слайд 4Двусторонняя симметрия
Под отражениями понимают любые зеркальные отражения — в точке, линии, плоскости.
Двусторонняя симметрия
Под отражениями понимают любые зеркальные отражения — в точке, линии, плоскости.

Слайд 5Нульмерная симметрия
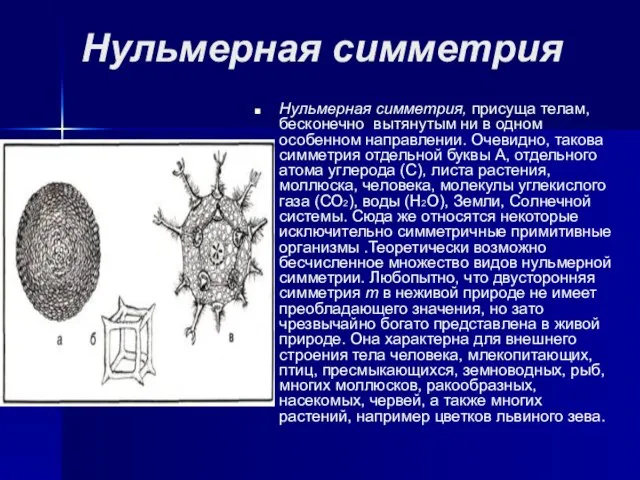
Нульмерная симметрия, присуща телам, бесконечно вытянутым ни в одном особенном направлении.
Нульмерная симметрия
Нульмерная симметрия, присуща телам, бесконечно вытянутым ни в одном особенном направлении.
Слайд 6Одномерная симметрия
Одномерная симметрия присуща телам, во-первых, вытянутым в одном каком-либо особенном направлении,
Одномерная симметрия
Одномерная симметрия присуща телам, во-первых, вытянутым в одном каком-либо особенном направлении,

Слайд 7Двумерная симметрия
Двумерной симметрией обладают тела, во-первых, вытянутые в двух взаимно перпендикулярных направлениях,
Двумерная симметрия
Двумерной симметрией обладают тела, во-первых, вытянутые в двух взаимно перпендикулярных направлениях,

Слайд 8Трехмерная симметрия
Трехмерная симметрия присуща телам, во-первых, вытянутым в трех взаимно перпендикулярных
Трехмерная симметрия
Трехмерная симметрия присуща телам, во-первых, вытянутым в трех взаимно перпендикулярных

Слайд 9Дисимметрические объекты
Объекты, симметрия которых исчерпывается лишь простыми (круговыми), или (и) переносными (трансляционными),
Дисимметрические объекты
Объекты, симметрия которых исчерпывается лишь простыми (круговыми), или (и) переносными (трансляционными),

Слайд 10Формы дисимметрических объектов
Дисимметрические объекты могут существовать в двух разновидностях: в виде оригинала
Формы дисимметрических объектов
Дисимметрические объекты могут существовать в двух разновидностях: в виде оригинала

Слайд 11Биологическая изомерия
Самое главное достижение — создание теории строения П- и Л-биообъектов. На
Биологическая изомерия
Самое главное достижение — создание теории строения П- и Л-биообъектов. На

Слайд 12Частота встреч П- и Л-формы биообъектов.
Как часто встречаются П- и
Частота встреч П- и Л-формы биообъектов.
Как часто встречаются П- и

Слайд 13Свойства П- и Л-форм.
Основное достижение — это открытие дисимметрии жизни
Свойства П- и Л-форм.
Основное достижение — это открытие дисимметрии жизни

Слайд 14Причина свойств П- и Л-форм
Никакой теории, отвечающей на этот вопрос, пока не
Причина свойств П- и Л-форм
Никакой теории, отвечающей на этот вопрос, пока не

Слайд 15Интересный факт
Много интересных фактов может сообщить наука о симметрии и о
Интересный факт
Много интересных фактов может сообщить наука о симметрии и о

Слайд 16Заключение
Конечно, смена видов симметрии по мере эволюции жизни происходила не только
Заключение
Конечно, смена видов симметрии по мере эволюции жизни происходила не только

 Вводный инструктаж по технике безопасности на уроках физической культуры
Вводный инструктаж по технике безопасности на уроках физической культуры ВПР по математике 5 класс
ВПР по математике 5 класс Философия мечты
Философия мечты Неформальные движения молодёжи
Неформальные движения молодёжи Чувство прекрасного
Чувство прекрасного Концептуальные основы корпоративной социальной ответственности
Концептуальные основы корпоративной социальной ответственности  Потолочная система охлаждения панельного типа Uponor Comfort
Потолочная система охлаждения панельного типа Uponor Comfort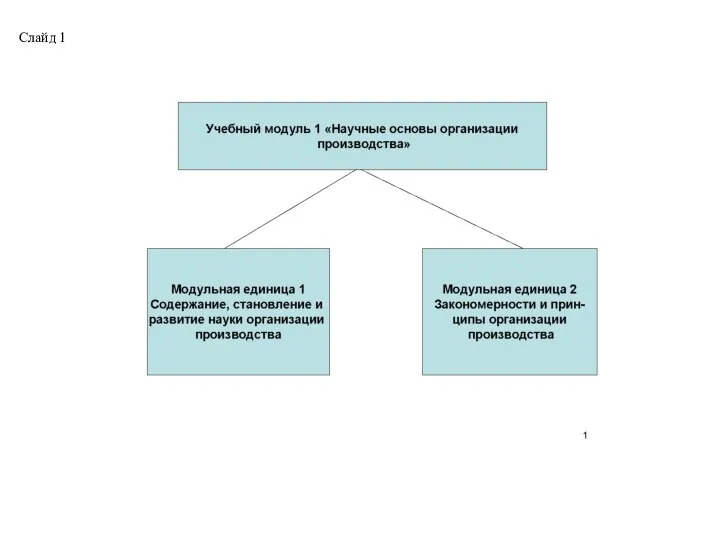 Тема 1.1.Организация производства как система научных знаний
Тема 1.1.Организация производства как система научных знаний Кафтан Урок №4
Кафтан Урок №4 Көксерек в театре
Көксерек в театре Моря Атлантического океана
Моря Атлантического океана Сходство и различие фразеологизмов и пословиц
Сходство и различие фразеологизмов и пословиц Кинесика как составной элемент невербальной коммуникации
Кинесика как составной элемент невербальной коммуникации Правовое регулирование оборота земель сельскохозяйственного назначения
Правовое регулирование оборота земель сельскохозяйственного назначения Гражданственность
Гражданственность Естественный ядерный реактор Окло
Естественный ядерный реактор Окло Презентация на тему Реки России
Презентация на тему Реки России План местности. Условные знаки
План местности. Условные знаки 10 години в 10 минути Христина Машкова “Четиринадесети рекламен форум”
10 години в 10 минути Христина Машкова “Четиринадесети рекламен форум” Моё блюдо: Яичница с овощами
Моё блюдо: Яичница с овощами Энде Михаэль Андреас Гельмут 1929-1995
Энде Михаэль Андреас Гельмут 1929-1995 Изменение состояния региональной гемодинамики у больных с ОАСНК с различной тяжестью ишемии нижних конечностей при лечении мето
Изменение состояния региональной гемодинамики у больных с ОАСНК с различной тяжестью ишемии нижних конечностей при лечении мето Русская кухня
Русская кухня Решение задач
Решение задач Исследование статической устойчивости асинхронной нагрузки при питании их от шин бесконечной мощности
Исследование статической устойчивости асинхронной нагрузки при питании их от шин бесконечной мощности Презентация на тему Инфаркт миокарда
Презентация на тему Инфаркт миокарда  Lecture 1
Lecture 1 Правда или ложь
Правда или ложь