Симметрия вокруг нас.

Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре
А
В
С
D
а
АВСD - квадрат

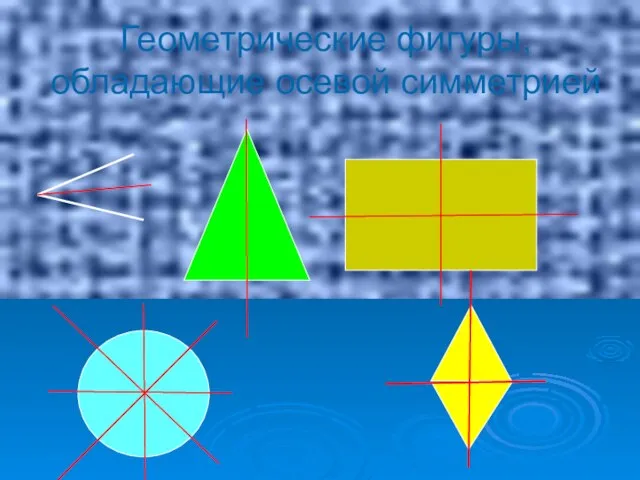
Геометрические фигуры, обладающие осевой симметрией

Фигуры, обладающие осевой симметрией

А
Сколько осей симметрии имеет:
Отрезок
Прямая
Луч
А
В
а
О
Е
одна
множество
Ни одной
Задачи:

Две точки А и А1 называются симметричными относительно точки О, если О – середина отрезка АА1.
О - центр симметрии
А
О
А1

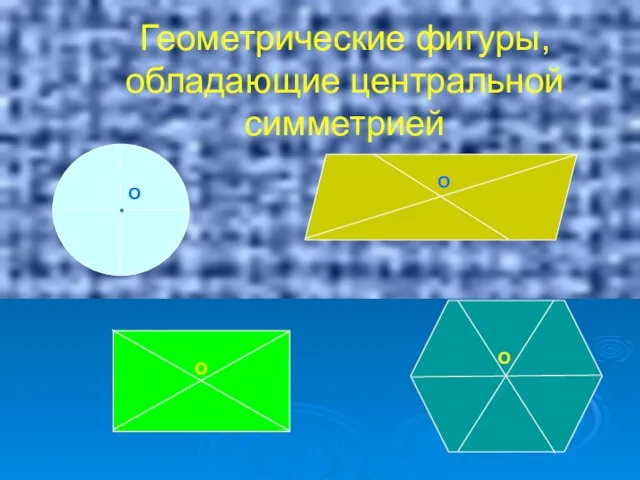
Геометрические фигуры, обладающие центральной симметрией
О
О
О
О

Фигуры, обладающие центральной симметрией

Зеркальная симметрия.
Одна половина объекта является зеркальным двойником по отношению к другой его половине. Такой объект называется зеркально симметричными.

Храм
Симметрия – это гармония…

Осевая симметрия ещё называется зеркальной…
Зеркало

Что такое орнаменты?
Орнаменты с давних времён применяются в декоративном искусстве. Так – же при исследовании геометрического строения кристаллов выяснилось, что их атомы расположены очень правильным образом, образуя как бы пространственный орнамент. По сути, именно это открытие побудило в конце девятнадцатого века физиков и математиков подробнее изучить орнаменты. Тогда и было дано точное математическое определение орнамента:
Орнамент – это бесконечная плоская фигура Ф, которая называется плоским орнаментом, если выполнены следующие условия:
среди перемещений, отображающих Ф на себя, существуют неколлинеарные параллельные переносы;
среди всех векторов (параллельных переносов), отображающих Ф. на себя, существует вектор наименьшей длины.

Паркеты.
Паркетом называется разбиение плоскости на многоугольники, при котором каждые два многоугольника либо не пересекаются, либо имеют одну общую вершину, либо имеют общую сторону, причем объединение сторон всех многоугольников является плоским орнаментом. Паркет называется правильным, если все многоугольники разбиения правильные (возможно, с различным числом сторон) и любую вершину паркета можно перевести в любую его вершину некоторым перемещением, отображающим весь паркет на себя.

Полотенце. Деталь вышивки. Конец XIX в. Новгородская губерния, Устюженский уезд. Двустороннее шитье.
Орнаменты восточных народов: индийские, китайские, японские.