Содержание
- 2. Краткое содержание предыдущих семинаров Уткин П.С. Нелинейные вычислительные процессы. Семинар № 5. Семинар № 1 (07.02.14).
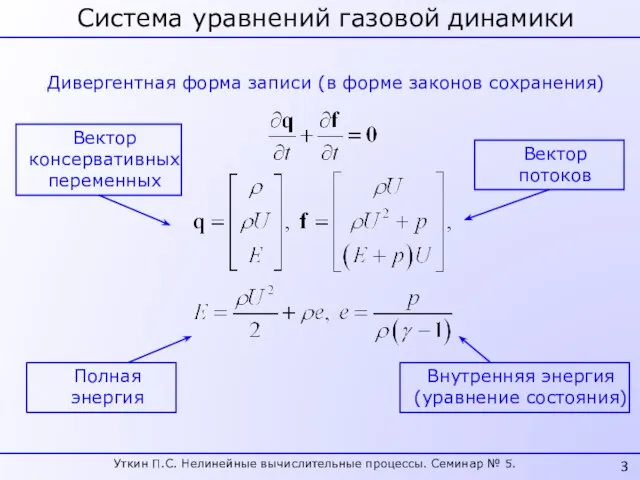
- 3. Система уравнений газовой динамики Дивергентная форма записи (в форме законов сохранения) Вектор консервативных переменных Вектор потоков
- 4. Анализ системы уравнений газовой динамики Характеристическая форма Скорость звука Матрица Якоби Куликовский А.Г., Погорелов Н.В., Семенов
- 5. Гиперболическая система уравнений Наличие конечной скорости распространения бесконечно слабых возмущений Возможность существования разрывных решений даже для
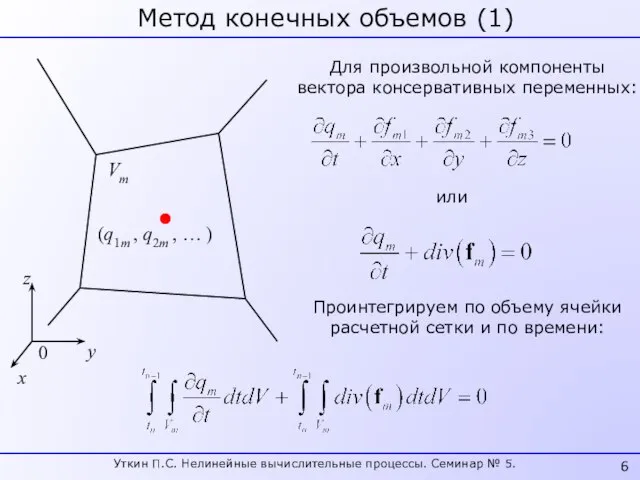
- 6. Метод конечных объемов (1) Vm (q1m , q2m , … ) 0 x y z Для
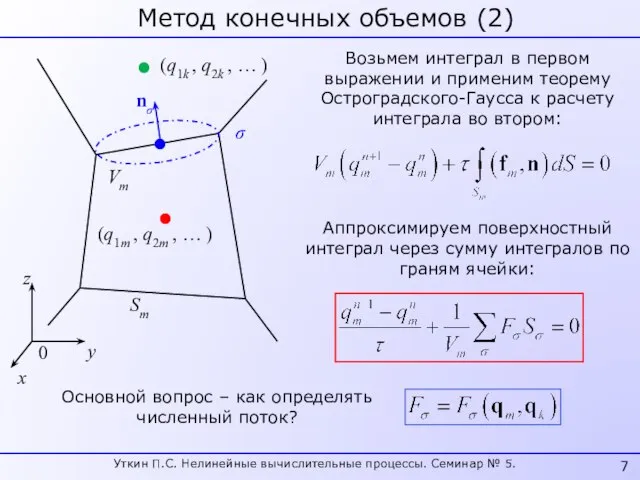
- 7. Метод конечных объемов (2) Vm (q1m , q2m , … ) σ nσ 0 x y
- 8. Постановка задачи о распаде произвольного разрыва Задача Коши для системы уравнений газовой динамики с разрывом первого
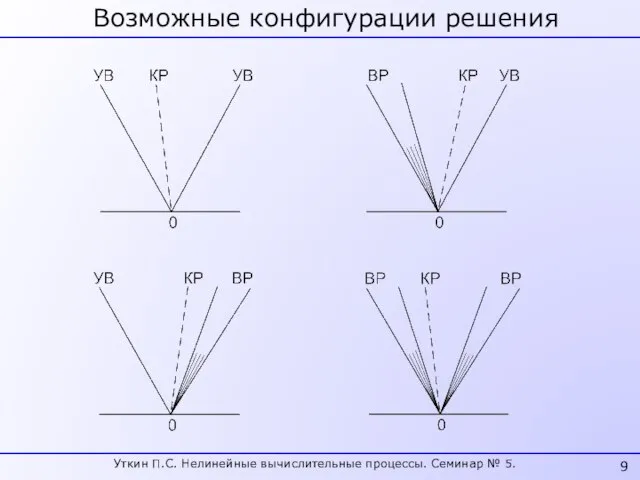
- 9. Возможные конфигурации решения Уткин П.С. Нелинейные вычислительные процессы. Семинар № 5.
- 10. Соотношения на разрыве Соотношения Ренкина – Гюгонио: Разрывы Контактные – нет потока массы вещества через разрыв
- 11. Элементарная теория ударных волн Адиабата Гюгонио p p0 адиабата Гюгонио адиабата Пуассона В ударной волне газ
- 12. Соотношения для ударных волн и волн разрежения «левая» УВ «правая» УВ «левая» ВР «правая» ВР Уткин
- 13. Метод Ньютона для нахождения давления на контактном разрыве Уткин П.С. Нелинейные вычислительные процессы. Семинар № 5.
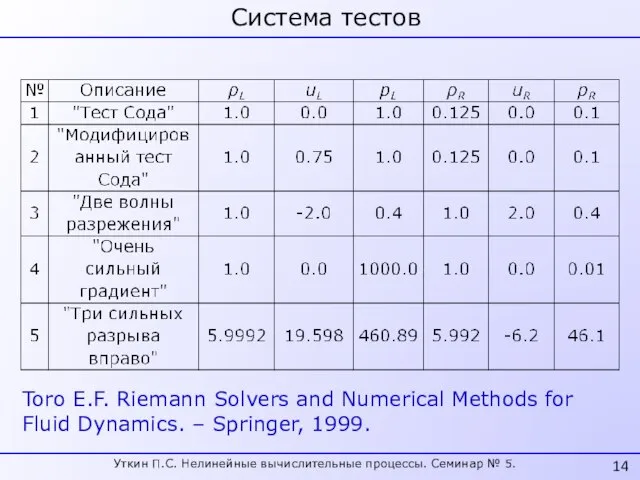
- 14. Система тестов Toro E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics. – Springer, 1999. Уткин
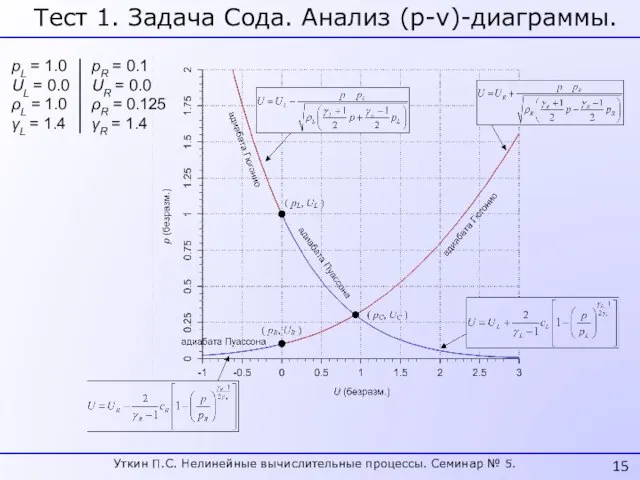
- 15. Тест 1. Задача Сода. Анализ (p-v)-диаграммы. pL = 1.0 UL = 0.0 ρL = 1.0 γL
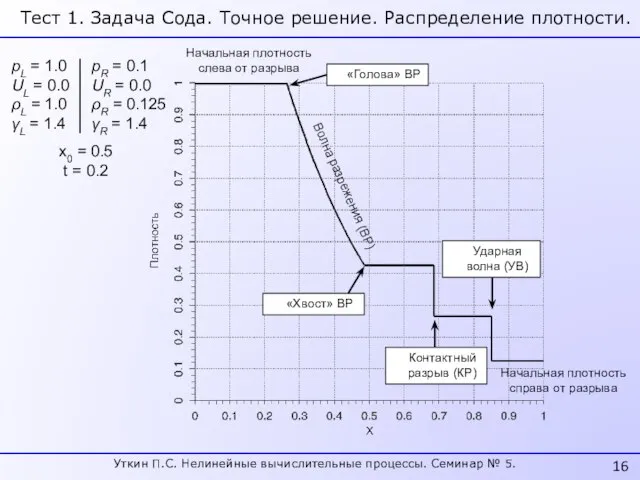
- 16. Тест 1. Задача Сода. Точное решение. Распределение плотности. Начальная плотность слева от разрыва Начальная плотность справа
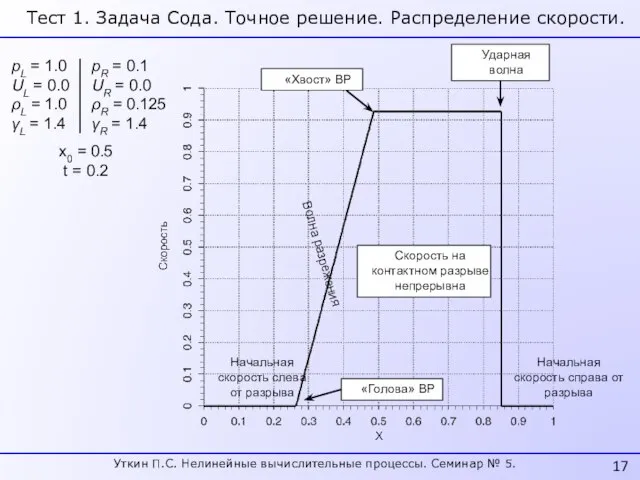
- 17. Начальная скорость слева от разрыва Начальная скорость справа от разрыва Ударная волна Скорость на контактном разрыве
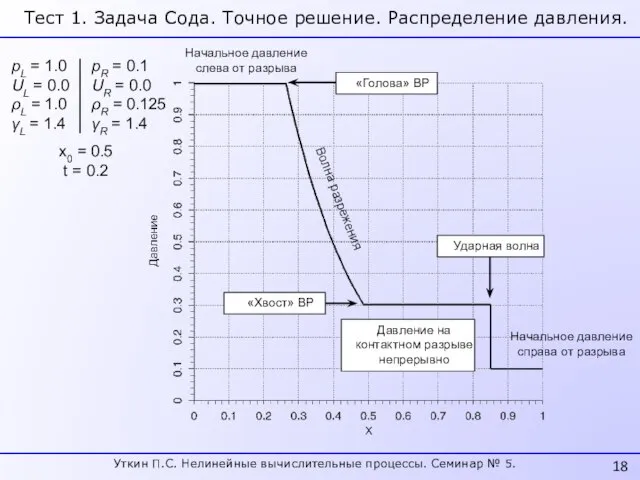
- 18. Начальное давление слева от разрыва Начальное давление справа от разрыва Ударная волна Давление на контактном разрыве
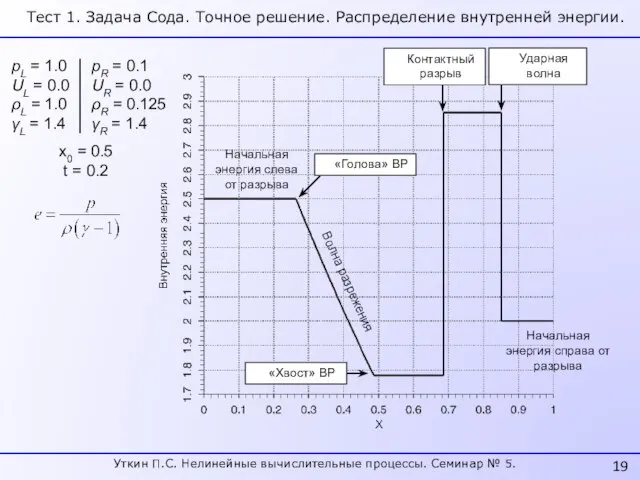
- 19. Начальная энергия слева от разрыва Начальная энергия справа от разрыва Ударная волна Волна разрежения «Голова» ВР
- 20. Алгоритм построения точного решения 1. Определяем по (p-v)-диаграмме конфигурацию, возникающую при распаде. 2. В результате решения
- 21. Тестирование схемы С.К. Годунова решения уравнений газовой динамики Сергей Константинович Годунов род. 1929 г., академик РАН
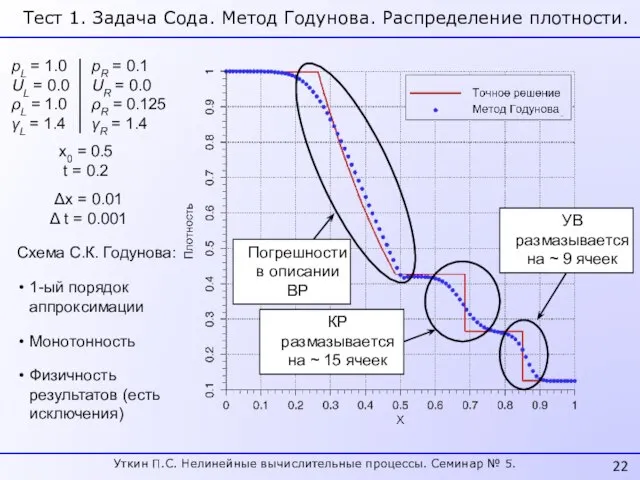
- 22. pL = 1.0 UL = 0.0 ρL = 1.0 γL = 1.4 pR = 0.1 UR
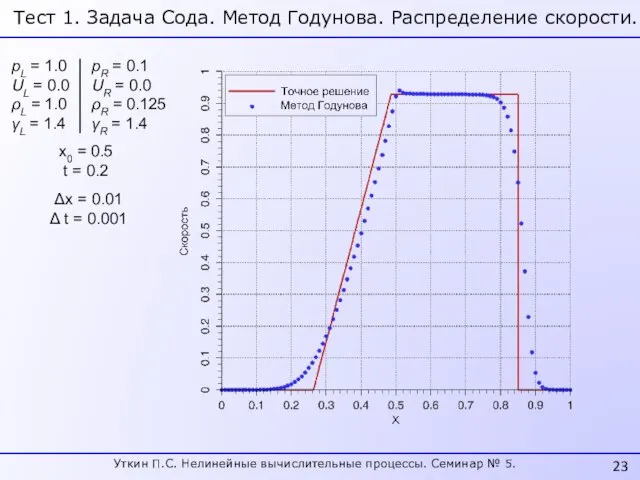
- 23. pL = 1.0 UL = 0.0 ρL = 1.0 γL = 1.4 pR = 0.1 UR
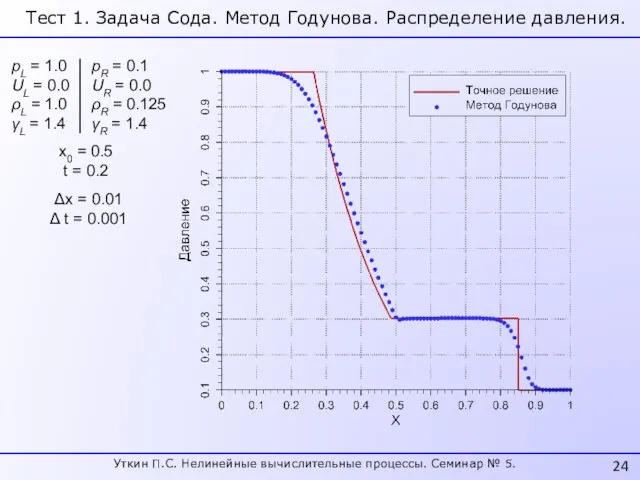
- 24. pL = 1.0 UL = 0.0 ρL = 1.0 γL = 1.4 pR = 0.1 UR
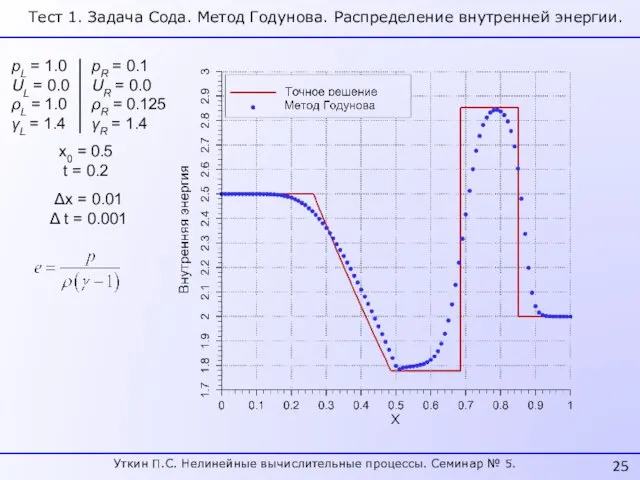
- 25. pL = 1.0 UL = 0.0 ρL = 1.0 γL = 1.4 pR = 0.1 UR
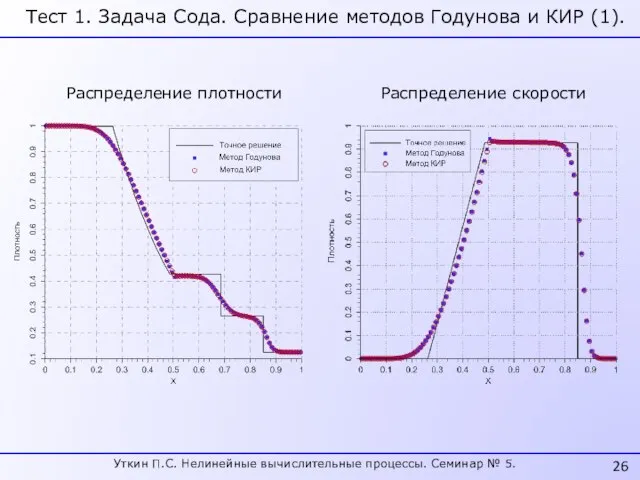
- 26. Тест 1. Задача Сода. Сравнение методов Годунова и КИР (1). Распределение плотности Распределение скорости Уткин П.С.
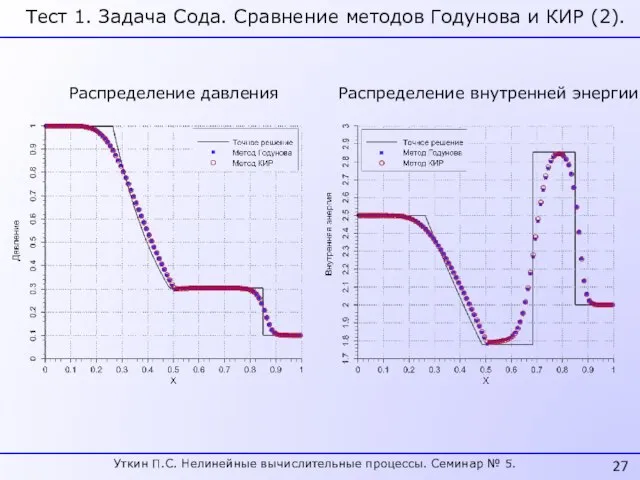
- 27. Тест 1. Задача Сода. Сравнение методов Годунова и КИР (2). Распределение давления Распределение внутренней энергии Уткин
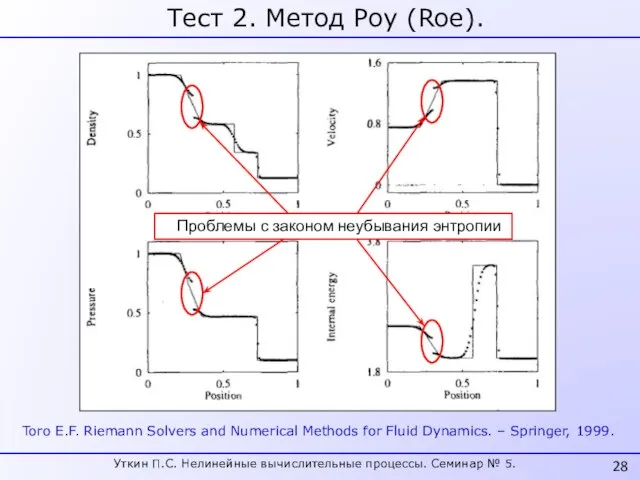
- 28. Тест 2. Метод Роу (Roe). Toro E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics. –
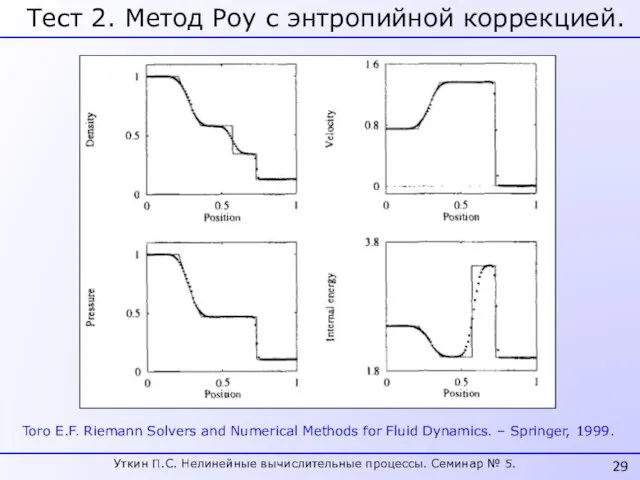
- 29. Тест 2. Метод Роу с энтропийной коррекцией. Toro E.F. Riemann Solvers and Numerical Methods for Fluid
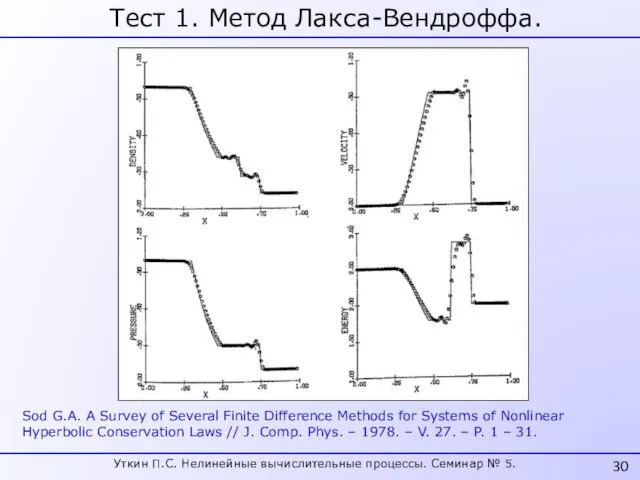
- 30. Тест 1. Метод Лакса-Вендроффа. Sod G.A. A Survey of Several Finite Difference Methods for Systems of
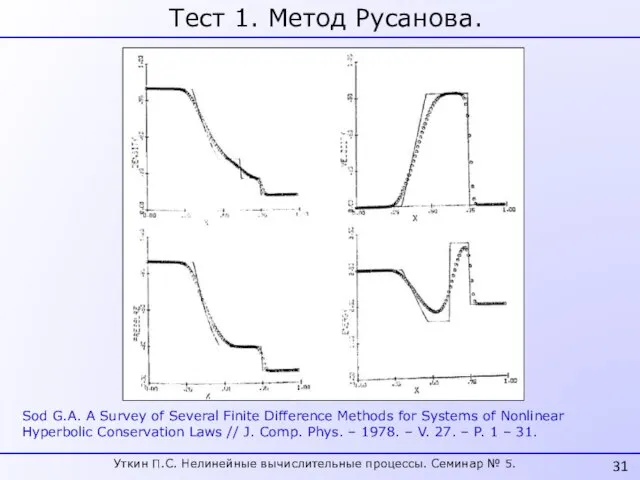
- 31. Тест 1. Метод Русанова. Sod G.A. A Survey of Several Finite Difference Methods for Systems of
- 33. Скачать презентацию










 Конфликт как форма коммуникации
Конфликт как форма коммуникации Střední odborná škola podnikatelská PROFIT, s.r.o
Střední odborná škola podnikatelská PROFIT, s.r.o Гибкость и ее развитие
Гибкость и ее развитие Sap Ustavınıń tiykarǵı qaǵıydaları. Áskerdiń sapqa turıwdan aldıngı hám saptagı wazıypaları
Sap Ustavınıń tiykarǵı qaǵıydaları. Áskerdiń sapqa turıwdan aldıngı hám saptagı wazıypaları Инвестиционная деятельность и жилищное строительство
Инвестиционная деятельность и жилищное строительство Цікаві факти про Азовське море
Цікаві факти про Азовське море Античный скептицизм
Античный скептицизм Презентация
Презентация Удмуртский этнотуристический центр эштэрек
Удмуртский этнотуристический центр эштэрек Организация и проведение государственной итоговой аттестации по образовательным программам основного образования в 2018 году
Организация и проведение государственной итоговой аттестации по образовательным программам основного образования в 2018 году Особенности формирования требований информационной безопасности Реестра источников ионизирующего излучения (ИИИ), которые могут
Особенности формирования требований информационной безопасности Реестра источников ионизирующего излучения (ИИИ), которые могут Мулькиет ялгъамаларнынъ имлясы
Мулькиет ялгъамаларнынъ имлясы Общая характеристика институтов права: право собственности и обязательное право
Общая характеристика институтов права: право собственности и обязательное право 4
4 What colour is it? (Цвета, какой это цвет?)
What colour is it? (Цвета, какой это цвет?) Иллюстрационный материал к выпускной квалификационной работе: Совершенствование управления оборотными средствами
Иллюстрационный материал к выпускной квалификационной работе: Совершенствование управления оборотными средствами История многовековой дружбы народов России и Болгарии
История многовековой дружбы народов России и Болгарии Парный натюрморт Чайный (часть 1)
Парный натюрморт Чайный (часть 1) Лечение болей при диабетической полиневропатии с помощью аппарата HiToP®gbo Medizintechnik AG
Лечение болей при диабетической полиневропатии с помощью аппарата HiToP®gbo Medizintechnik AG Тема: "Адаптация ребенка к обучению в школе"
Тема: "Адаптация ребенка к обучению в школе" Моя малая Родина
Моя малая Родина Ravnomernoe_dvizhenie_po_okruzhnosti
Ravnomernoe_dvizhenie_po_okruzhnosti 经理对我印象不错
经理对我印象不错 Характеристика планет Солнечной Системы и НЕКОТОРЫХ известных звёзд
Характеристика планет Солнечной Системы и НЕКОТОРЫХ известных звёзд Мировая практика выбора конструкций ВЭУ, их влияние на экономические характеристикии выбор ВЭУ для России
Мировая практика выбора конструкций ВЭУ, их влияние на экономические характеристикии выбор ВЭУ для России Помилуй! И помилован будешь…
Помилуй! И помилован будешь… «1С:Предприятие 8. Медицина. Клиническая лаборатория»
«1С:Предприятие 8. Медицина. Клиническая лаборатория» Нумерация в пределах тысячи
Нумерация в пределах тысячи