системы счисления, используемые в компьютере

СОДЕРЖАНИЕ
ЧТО ТАКОЕ СИСТЕМА СЧИСЛЕНИЯ…………...………………3
ВВЕДЕНИЕ…………………………………………………………..4
СИСТЕМА СЧИСЛЕНИЯ (СС)……………………………..…..5-10
ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ….…………….11-20
ПЕРЕВОД ЧИСЕЛ ПОЗИЦИОННЫХ СИСТЕМАХ СЧИСЛЕНИЯ……………………………………………………21-28
ВЫВОДЫ………………………………...….......………………….29
Список литературы…………………………………………...……30

01

Система счисления (СС)
Знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.

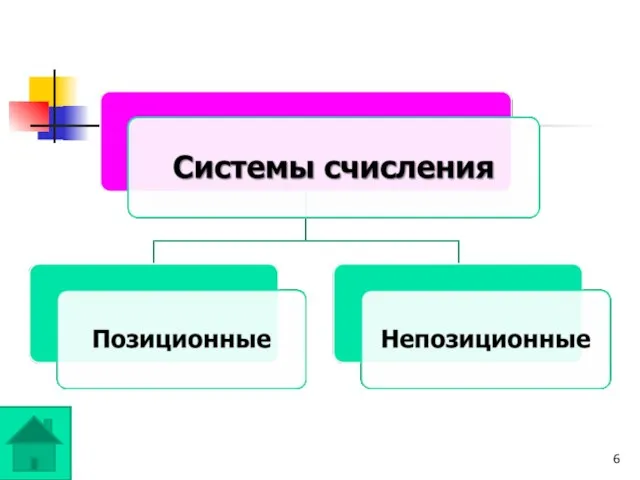
Позиционная система счисления
Количественное значение каждой цифры зависит от ее местоположения (позиции) в числе.

Непозиционная система счисления
Цифры не меняют своего количественного значения при изменении их положения в числе.

Основание системы
Количество цифр, используемых для изображения числа в позиционной системе счисления.

Алгоритм перевода десятичных чисел в двоичные
Разделить число на 2. Зафиксировать остаток (0 или 1) и частное.
Если частное не равно 0, то разделить его на 2, и так далее, пока частное не станет равно 0.
Если частное 0, то записать все полученные остатки, начиная с первого, справа налево.

Позиционные системы счисления

В позиционных системах счисления основание системы равно количеству цифр (знаков в ее алфавите) и определяет, во сколько раз различаются значения одинаковых цифр, стоящих в соседних позициях числа.

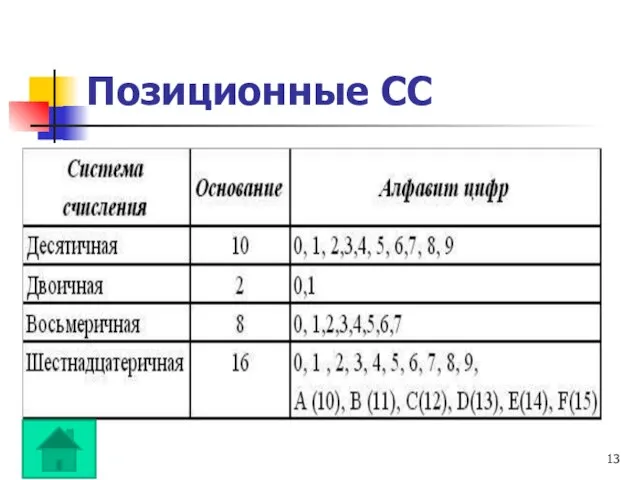
Позиционные СС

Разряд
Позиция цифры в числе.
Возрастает справа налево, от младших разрядов к старшим.

В десятичной СС цифра, находящаяся в крайней справа позиции (разряде), обозначает количество единиц, цифра, смещенная на одну позицию влево, — количество десятков, еще левее — сотен, затем тысяч и так далее.

Пример
55510 = 5·102+5·101+5·100

Умножение или деление десятичного числа на 10 (величину основания) приводит к перемещению запятой, отделяющей целую часть от дробной, на один разряд соответственно вправо или влево.

Двоичная СС
Числа в двоичной системе в развернутой форме записываются в виде суммы степеней основания 2 с коэффициен-тами, в качестве которых выступают цифры 0 или 1.

Умножение или деление двоичного числа на 2 (величину основания) приводит к перемещению запятой, отделяющей целую часть от дробной на один разряд соответственно вправо или влево.

Пример
101,012 · 2 = 1010,12;
101,012 : 2 = 10,1012

Перевод чисел
в позиционных системах счисления

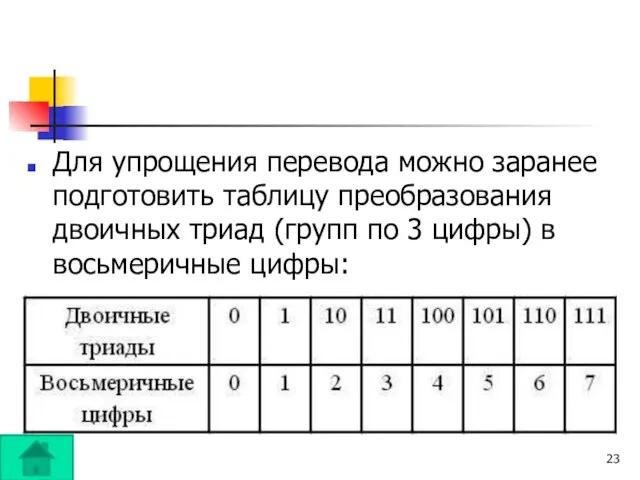
Для перевода целого двоичного числа в восьмеричное его нужно разбить на группы по три цифры, справа налево, а затем преобразовать каждую группу в восьмеричную цифру.
Если в последней, левой, группе окажется меньше трех цифр, то необходимо ее дополнить слева нулями.
+

Для упрощения перевода можно заранее подготовить таблицу преобразования двоичных триад (групп по 3 цифры) в восьмеричные цифры:

Для перевода дробного двоичного числа (правильной дроби) в восьмеричное необходимо разбить его на триады слева направо и, если в последней, правой, группе окажется меньше трех цифр, дополнить ее справа нулями.
Далее необходимо триады заменить на восьмеричные числа.

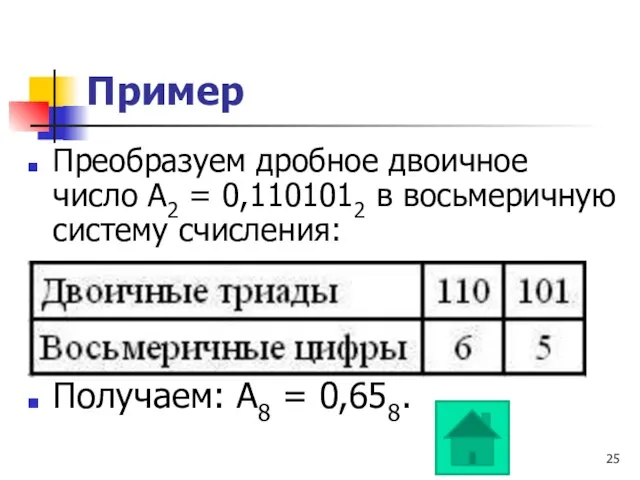
Пример
Преобразуем дробное двоичное число А2 = 0,1101012 в восьмеричную систему счисления:
Получаем: А8 = 0,658.

При сложении двух единиц происходит переполнение разряда и производится перенос в старший разряд.
Переполнение разряда наступает тогда, когда величина числа в нем становится равной или большей основания.

Сложим в столбик двоичные числа 1102 и 112

Вычитание