Скалярное произведение векторов

Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.

Числа называют скалярами. Поэтому само название «скалярное» говорит о том, что скалярное произведение двух векторов это число, которое ставится в соответствие этим векторам по определённому правилу.

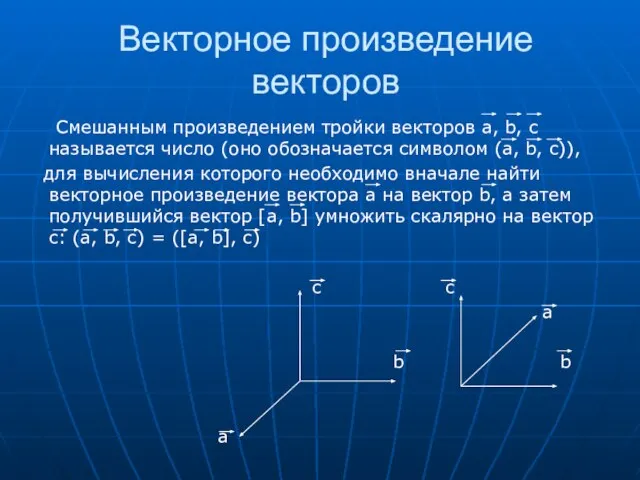
Векторное произведение векторов
Смешанным произведением тройки векторов а, b, c называется число (оно обозначается символом (a, b, c)),
для вычисления которого необходимо вначале найти векторное произведение вектора а на вектор b, а затем получившийся вектор [a, b] умножить скалярно на вектор c: (a, b, c) = ([a, b], c)
c c
a
b b
a

Векторная алгебра
Найти значение x
Задание:
а = {4, 5, 1}, b = {1, 1, -4}
C = {3, -3, 1} d = {1, 2, -5}
X=([a + b + c], a).

Находим сумму векторов a, b, c и умножаем на вектор d:
a + b + c = {8, 3, -2}
d = {1, 2, -5}

Векторное произведение этих векторов можно найти с помощью определителя третьего порядка:
i j k -11
8 3 -2 = 38
1 2 -5 13