Соколов А.П.ТЕОРЕТИЧЕСКАЯ МЕХАНИКА(часть 1)

ПОЛОЖЕНИЕ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ
В СТРУКТУРЕ ООП
(Основная образовательная программа)

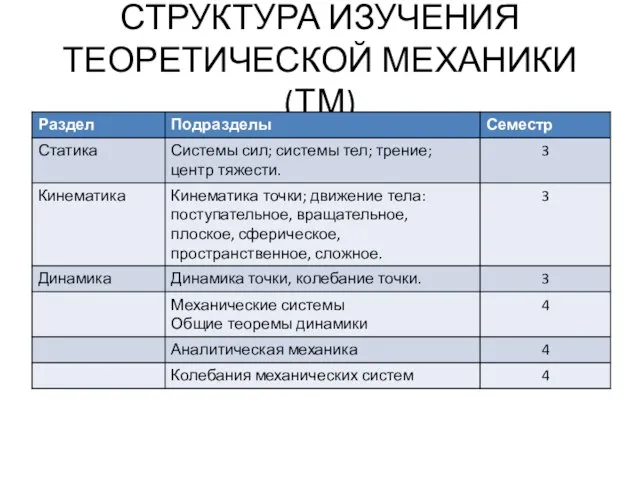
СТРУКТУРА ИЗУЧЕНИЯ
ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ (ТМ)

ЦЕЛИ ИЗУЧЕНИЯ ТМ
(по рабочей программе)
В результате освоения данной дисциплины бакалавр приобретает знания, умения и навыки, обеспечивающие достижение целей основной образовательной программы «Теплоэнергетика и теплотехника».
Дисциплина нацелена на подготовку бакалавров к решению следующих профессиональных задач:
– сбор и анализ информационных исходных данных для проектирования тепловых электрических станций; систем теплоэнергоснабжения, топливоснабжения установок, цехов промышленных предприятий и объектов жилищно-коммунального хозяйства (ЖКХ); устройств и систем автоматизации и управления;
– расчет и проектирование деталей и узлов в соответствии с техническим заданием с использованием стандартных средств автоматизации проектирования;
– разработка проектной и рабочей технической документации, оформление законченных проектно-конструкторских работ;
– изучение научно-технической информации, отечественного и зарубежного опыта по тематике исследования;
– проведение экспериментов по заданной методике и анализ результатов;
– проведение измерений и наблюдений, составление описания проводимых исследований, подготовка данных для составления обзоров, отчетов и научных публикаций;
– составление отчета по выполненному заданию, участие во внедрении результатов исследований и разработок.

РАЗВИТИЕ МЕХАНИКИ СВЯЗАНО С РАСШИРЕНИЕМ КРУГА РЕШАЕМЫХ ПРАКТИЧЕСКИХ ЗАДАЧ.
До Аристотеля (384 – 322 гг. до Р.Х.) не существовало деления науки по отраслям знаний. Только после него начинается процесс выделения частных наук из общего естествознания.
Становление механики как науки связывают с Архимедом (287-212 гг. до Р.Х.). Он дал точное решение задачи о равновесии сил, приложенных к рычагу, создал учение о центре тяжести тел и сформулировал закон о гидростатическом давлении жидкости на погружённое в него тело.
Гениальный представитель эпохи Возрождения Леонардо да Винчи (1451-1519) изучил движение падающего тела, движение тела по наклонной плоскости, явление трения и ввёл понятие момента силы.
В целом развитие механики шло от опыта работы с механизмами через обобщение выявляемых закономерностей к определению строгих законов, по чёткости близким к математическим законам. В виду такой строгости теоретическую механику вполне правомерно можно назвать математической механикой. Высокая степень абстрагирования от свойств реальных объектов позволила систематизировать правила анализа механических систем и произвела своеобразную стандартизацию этих правил. С другой стороны математический подход, к которому тяготеет теоретическая механика, требует оговаривать все упрощения, допускаемые в решении каждой конкретной задачи. Невыполнение данного требования порождает подозрение в ненаучном решении конкретной технической задачи.

МОДЕЛИРОВАНИЕ – ГЛАВНОЕ НАПРАВЛЕНИЕ РАЗВИТИЯ ТМ
Общим во всех этих умениях является умение анализировать техническую задачу с позиций механики, т.е. умение разбивать реальную механическую систему на блоки, выявлять закономерности их взаимодействия и определять оптимальные условия функционирования всей системы

АБСТРАКТНЫЕ МОДЕЛИ РЕАЛЬНЫХ ТЕЛ
В теоретической механике изучается движение одних тел относительно других тел, которые принимаются за системы отсчёта. Задача теоретической механики не только описывать, но и предсказывать движение тел, устанавливая причинные связи в определённом, весьма широком, круге явлений.
В теоретической механике вводят абстрактные модели, которые приближённо отражают свойства реальных систем. Степень приближения, т.е. точность механической модели, обуславливается конкретной задачей.

ОСНОВНЫЕ АБСТРАКТНЫЕ МОДЕЛИ РЕАЛЬНЫХ ТЕЛ
1.Материальная точка – тело, размерами которого можно пренебречь в рамках конкретной задачи;
2.Абсолютно твёрдое тело – объём конечных размеров, сплошь заполненный веществом, , причём расстояния между любыми двумя точками среды, заполняющей объём, не изменяются во время движения;
3.Сплошная деформируемая среда – заполняет конечный объём или неограниченное пространство; расстояния между точками такой среды могут меняться.
Сравнивая два последних определения, можно сказать, что сплошная деформируемая среда – это деформируемое твёрдое тело.
Из абстрактных моделей реальных тел могут образовываться системы, например: система свободных тел; системы со связями; абсолютно твёрдое тело с полостью, заполненной жидкостью, и т.п. Исходя из определения системы тел, можно сказать, что абсолютно твёрдое тело – это система тел с такими связями, при которых, расстояние между двумя точками системы постоянно.

ВЫРОЖДЕННЫЕ МОДЕЛИ
бесконечно тонкий стержень – стержень, который «работает» только на растяжение и сжатие, но не «работает» на изгиб;
бесконечно тонкая пластина;
невесомые стержни и нити, связывающие между собой материальные точки, и т.д.
ВЫРОЖДЕННАЯ МОДЕЛЬ – ЭТО ЧАСТНЫЙ СЛУЧАЙ ОБЩЕЙ МОДЕЛИ ПРИ УМЕНЬШЕНИИ ЕЁ СВОЙСТВ. Так общий случай – стержень, теряя толщину, перестаёт работать на изгиб как балка и превращается в бесконечно тонкий стержень.

СВОЙСТВА ПРОСТРАНСТВА
(для идеальных условий)
Свойства пространства были постулированы при решении задач астрономии, т.е. для идеальных условий, когда нет трения. В этом случае полагают, что пространство однородно и изотропно. Однако, из опытов выявлено, что механические явления протекают неодинаково в разных местах физической системы отсчёта и неодинаково в различных направлениях. Это позволило сформулировать понятия: неоднородность и анизотропность
Неоднородность – это зависимость характера протекания явления от места, в котором мы наблюдаем это явление.
Анизотропность (неизотропность) – это зависимость характера движения от направления. Примеры: течение реки по меридиану (с севера на юг - Волга); полёт снаряда, маятник Фуко.

СВОЙСТВА ПРОСТРАНСТВА
(для реальных условий)
При решении задач в реальных условиях учитывается не только неоднородность и неизотропность пространства. Гораздо в большей степени проявляется влияние трения. Приведение реальной, трудно рассчитываемой механической системы к идеальной по сути является идеологией. Идеализированные механические системы поддаются расчёту, а идеология облегчает изложение законов механики и упрощает поиск ошибок в анализе механических систем. Но идеология иногда формирует и тупиковые ситуации. Например, при малых колебаниях нелинейной системы её принимают за линейную, однако, условия устойчивости линейной и нелинейной систем не совпадают.

СИСТЕМЫ ОТСЧЁТА
Свойства системы отсчёта (неоднородность и анизотропность) затрудняют наблюдение за движением тела.
Практически свободна от этого – геоцентрическая система: центр системы в центре Земли и системы не вращается относительно «неподвижных» звёзд). Геоцентрическая система удобна для расчётов движений на Земле.
Для небесной механики (для тел солнечной системы): гелиоцентрическая система отсчёта, которая движется с центром масс Солнечной системы и не вращается относительно «неподвижных» звёзд. Для этой системы пока не обнаружены неоднородность и анизотропность пространства по отношению к явлениям механики.
Вводится абстрактная инерциальная система отсчёта, для которой пространство однородно и изотропно по отношению к явлениям механики

ИНЕРЦИАЛЬНАЯ СИСТЕМА ОТСЧЁТА
Инерциальная система отсчёта – такая, собственное движение которой не может быть обнаружено никаким механическим опытом.
Дополнение. Две системы отсчёта движутся относительно исходной прямолинейно, равномерно. Нельзя обнаружить движение одной системы относительно другой механическим путём только в том случае, если системы не взаимосвязаны.
Поиск не взаимосвязанных систем отсчёта – это идеология. На поверхности Земли все системы отсчёта взаимосвязаны.
Инерциальная система отсчёта – это модель, справедливая в рамках конкретной задачи.
Все системы отсчёта движущиеся относительно исходной прямолинейно, равномерно будут инерциальными. Это позволяет ввести единую декартовую систему координат. Такое пространство называется евклидовым.
Условное соглашение – берут правую систему координат (рис. 1).
Время – в классической (нерелятивистской) механике абсолютно, единое для всех систем отсчёта то есть начальный момент – произволен. В отличие релятивистской механики, где применяется принцип относительности.
Состояние движения системы в момент времени t определяется координатами и скоростями точек в этот момент.

.
Реальные тела взаимодействуют.
Сила – мера механического взаимодействия тел.
При взаимодействии меняется состояние движения системы.
Теоретическая механика изучает как силы взаимодействия меняют состояние движения системы.
В соответствии с идеологией изучения теоретической механики её изложение разбито на разделы:
Статика.
Кинематика.
Динамика.

ИДЕОЛОГИЯ И ПРИНЦИПЫ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ
Идеология ТМ
От простого к сложному
Принципы ТМ
В основе – система аксиом (на основе опыта, наблюдений)
Законы внутренней логики (относительная независимость теории)
Практика – контролёр верности теории

статика
Статика (от греч. στατικε - неподвижное) – раздел теоретической механики, в котором изучается равновесие тела или системы тел.
Аксиомы статики.
Связи и реакции.
Система сходящихся сил.
Пара сил.
Момент силы.
Основная теорема статики.
Плоская система сил.
Пространственная система сил.
Центр тяжести.
Трение скольжения.
Равновесие тел.
.
.

МОДЕЛИ, ИСПОЛЬЗУЕМЫЕ
В СТАТИКЕ
1. Материальная точка – геометрическая точка с массой;
2. Абсолютно твёрдое тело – совокупность материальных точек, расстояния между которыми не меняемся
3. Сила – мера механического взаимодействия тел, в результате которого изменяется их движение.
Поскольку в теоретической механике рассматривают только абсолютно твёрдые тела, то деформацией взаимодействующих тел пренебрегают. Поэтому и при взаимодействии тел рассматривается только изменение их движения.
Из математики взято понятие вектор. Оно наиболее подходит для описания действия сил. В этом описании указывается: линия действия силы, точка приложения силы и собственно вектор силы.
Следует обратить внимание, что если можно указать точку приложения силы, то говорят о сосредоточенной силе, в противном случае говорят о распределённой нагрузке. В реальных механических системах взаимодействие тел осуществляется по поверхности, и даже более точно – в участке объёма тела. Это очередной раз доказывает, что сила – это модель, но эта модель хорошо работает, если за точку приложения силы брать центр контактирующей поверхности тела.
.

ОПЕРАЦИИ С ВЕКТОРАМИ
1.Сложение векторов.
2.Вычитание векторов.
3.Умножение вектора на скаляр.
4.Проецирование вектора на декартовые оси.
5.Выражение вектора через проекции и единичные векторы.
6.Скалярное произведение векторов.
7.Векторное произведение векторов.

ПЕРВАЯ АКСИОМА СТАТИКИ
Из повседневного опыта: силы имеют векторный характер, то есть величину, направление, линию действия, точку приложения. Условие равновесия сил, действующих на твёрдое тело, сводится к свойствам систем векторов.
Обобщая опыт изучения физических законов природы, Галилей и Ньютон сформулировали основные законы механики, которые могут рассматриваться как аксиомы механики, так как имеют в своей основе экспериментальные факты.
Аксиома 1. Действие на точку твёрдого тела нескольких сил равносильно действию одной равнодействующей силы, строящейся по правилу сложения векторов (рис.3).
Следствие. Силы, приложенные к точке твёрдого тела, складываются по правилу параллелограмма.
.
Рис. 3

Вторая и третья аксиомы
Аксиома 2. Две силы, приложенные к твёрдому телу, взаимно уравновешиваются тогда и только тогда, когда они равны по величине, направлены в противоположные стороны и лежат на одной прямой.
Аксиома 3. Действие на твёрдое тело системы сил не изменится, если добавить к этой системе или отбросить от неё две силы, равные по величине, направленные в противоположные стороны и лежащие на одной прямой.
Следствие. Силу, действующую на точку твёрдого тела, можно переносить вдоль линии действия силы без изменения равновесия (то есть, сила является скользящим вектором, рис.4)
Рис. 4
.

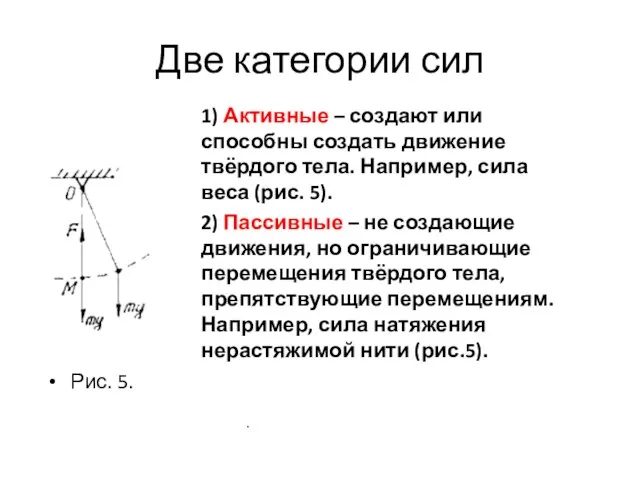
Две категории сил
.
Рис. 5.
1) Активные – создают или способны создать движение твёрдого тела. Например, сила веса (рис. 5).
2) Пассивные – не создающие движения, но ограничивающие перемещения твёрдого тела, препятствующие перемещениям. Например, сила натяжения нерастяжимой нити (рис.5).
.

АКСИОМЫ СТАТИКИ
(ПРОДОЛЖЕНИЕ)
Четвёртая аксиома
Действие одного тела на второе равно и противоположно действию этого второго тела на первое (действие равно противодействию).
Связи – тела, ограничивающие движение данного тела. Внутренние связи – взаимоограничение движения между телами внутри системы.
Пятая аксиома
Связи, наложенные на систему материальных точек, можно заменить силами реакций, действие которых эквивалентно действию связей.
Когда пассивные силы не могут уравновесить действие активных сил, начинается движение.

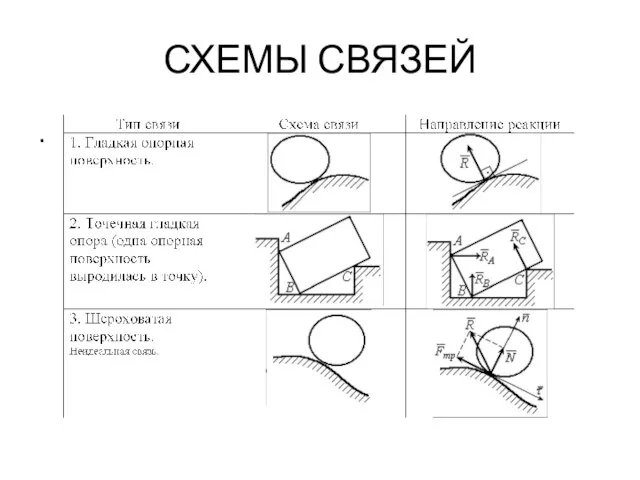
СВЯЗИ И РЕАКЦИИ
Связи – тела, ограничивающие движение данного тела.
Это определение сформулировано для случая одного тела. Если же рассматривается система тел, то практично ввести понятие внутренние связи – взаимоограничение движения между телами внутри системы.
Связи указывают на схемах механизмов условными обозначениями, из которых видно ограничение движения тела. Затем применяют принцип освобождения от связей.
Принцип освобождения от связей – связи мысленно отбрасывают, а их действие заменяют силами, направленными противоположно ограничению движения. Эти силы называют силами реакций или реакциями.

СХЕМЫ СВЯЗЕЙ
.

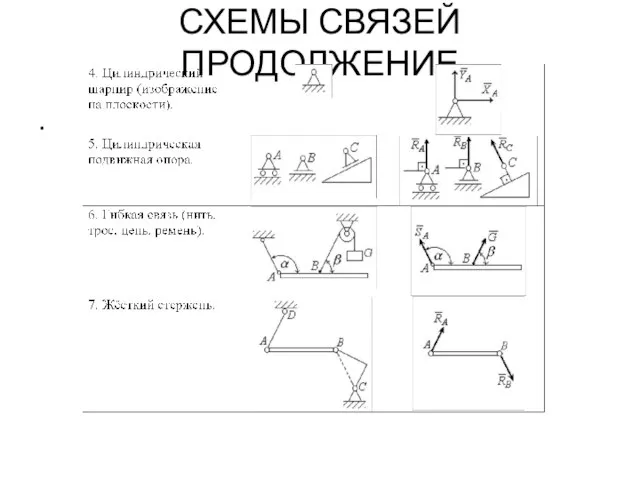
СХЕМЫ СВЯЗЕЙ ПРОДОЛЖЕНИЕ
.

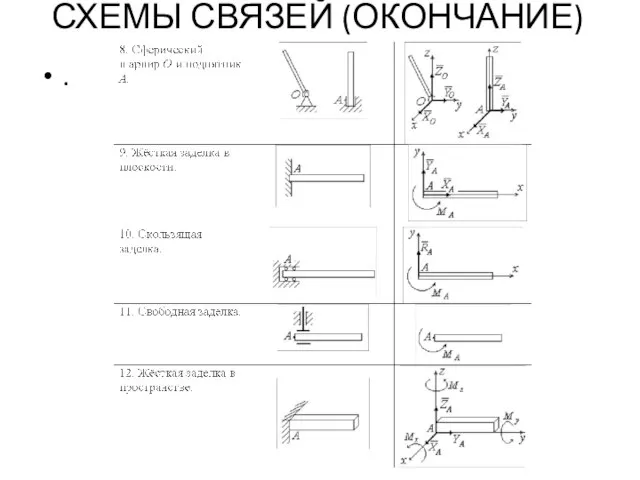
СХЕМЫ СВЯЗЕЙ (ОКОНЧАНИЕ)
.

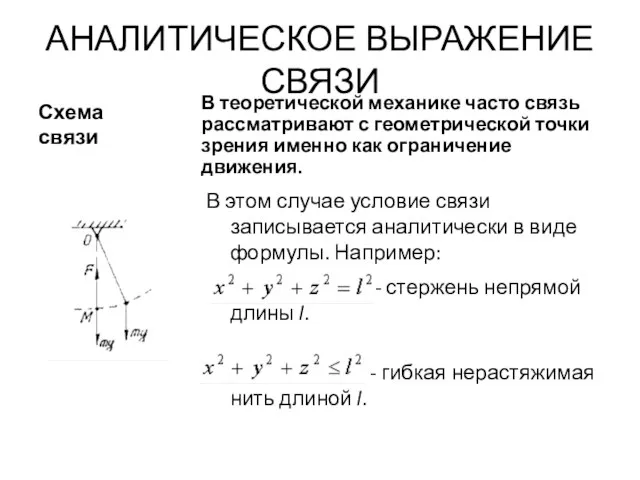
АНАЛИТИЧЕСКОЕ ВЫРАЖЕНИЕ СВЯЗИ
Схема связи
В теоретической механике часто связь рассматривают с геометрической точки зрения именно как ограничение движения.
В этом случае условие связи записывается аналитически в виде формулы. Например:
- стержень непрямой длины l.
- гибкая нерастяжимая нить длиной l.

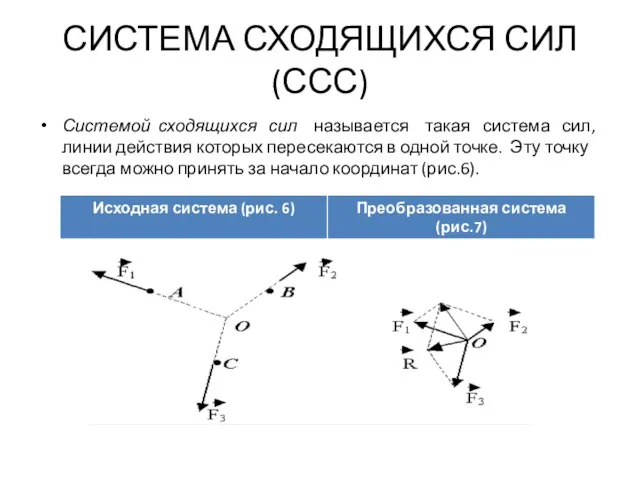
СИСТЕМА СХОДЯЩИХСЯ СИЛ (ССС)
Системой сходящихся сил называется такая система сил, линии действия которых пересекаются в одной точке. Эту точку всегда можно принять за начало координат (рис.6).

Приведение ССС к равнодействующей
Исходную систему сходящихся сил (рис. 6) можно преобразовать. На основании следствия третьей аксиомы статики точку приложения каждой силы перемещаем в точку О (рис. 7). Затем на основании первой аксиомы статики делаем следующие операции: складываем силы F1 и F2; к получившейся силе прибавляем F3; к получившейся силе прибавляем F4, и т.д.
В результате система сходящихся сил приводится к одной равнодействующей силе R (кратко, равнодействующая).

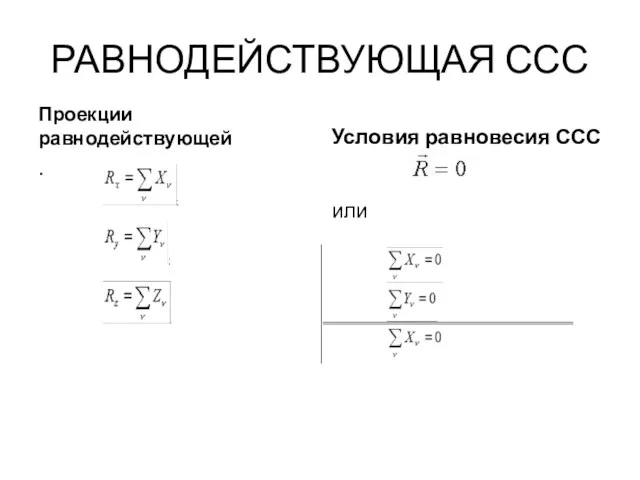
РАВНОДЕЙСТВУЮЩАЯ ССС
Проекции равнодействующей
.
Условия равновесия ССС
или

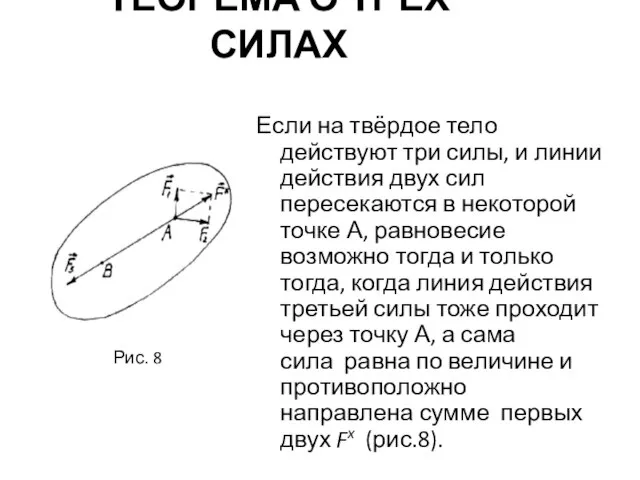
ТЕОРЕМА О ТРЁХ СИЛАХ
Если на твёрдое тело действуют три силы, и линии действия двух сил пересекаются в некоторой точке А, равновесие возможно тогда и только тогда, когда линия действия третьей силы тоже проходит через точку А, а сама сила равна по величине и противоположно направлена сумме первых двух Fx (рис.8).
Рис. 8

ПРИМЕРЫ НА ТЕОРЕМУ О ТРЁХ СИЛАХ
.
.
Задача 1. Груз M1 весом P (рис. 1.9) подвешен на гибком нерастяжимом тросе OM1, отклонённом от вертикали на угол α, и удерживается в равновесии с помощью другого нерастяжимого троса M1AM2, охватывающего идеальный блок A и несущего на свободном конце груз M2. Считая, что при равновесии участок троса M1A горизонтален, определить вес Q груза M1 и натяжение троса OM1. Размерами груза M1 и весом тросов пренебречь.
Решение. Рассмотрим равновесие груза M1. Активными силами являются вертикально направленная сила P и горизонтально направленная сила T2, равная по модулю весу груза Q, так как идеальны блок A изменяет только направление силы.
На груз M1 наложена связь, осуществляемая тросом OM1. Освободим его от связи. Реакция связи T1 направлена по тросу вверх. Таким образом, груз M1 находится в равновесии под действием плоской сходящейся системы трёх сил: P, T1 и T2, причём T2=Q (рис. 10).
.

РЕШЕНИЕ ЗАДАЧИ 1
.
.
Решим эту задачу двумя способами: геометрическим и аналитическим.
Геометрический способ. Так как точка M1 находится в равновесии под действием трёх сил, то силовой многоугольник, построенный на этих силах, должен быть замкнутым (рис. 11). Построение многоугольника следует начать с заданной силы P. Изобразив вектор P, проводим через его начало и конец прямые, параллельные направлением сил T1 и T2. Точка пересечения этих прямых определит третью вершину силового треугольника. Ориентация всех векторов должна быть такова, чтобы силовой треугольник был замкнутым. Это даст возможность проверить правильность направления неизвестных реакций.
Из силового треугольника находим
.

АНАЛИТИЧЕСКИЙ СПОСОБ
.
.
Выберем оси координат так, чтобы они совпадали с максимумом действующих сил, в этом случае уравнения равновесия будут иметь наипростейший вид.
Система приложенных сил P, T1 и T2 – плоская сходящаяся система, для которой существует два уравнения равновесия.
В полученной системе уравнений две неизвестные величины: T1 и T2, т.е. задача статически определима. Из этой системы уравнений находим:

Задача 2
Однородный цилиндр A весом P и радиусом r (рис. 12) опирается на гладкую поверхность цилиндра B радиусом R и удерживается в равновесии с помощью нити CD длиной l, расположенной в поперечной плоскости симметрии. Определить натяжение нити и реакцию цилиндрической поверхности.
Решение. Рассмотрим равновесие цилиндра A. На него действует сила P, направленная вертикально вниз. Связями являются гладкая цилиндрическая поверхность B и нить CD. Освободимся от связей. Реакция N цилиндрической поверхности направлена по общей нормали к цилиндрам и, следовательно, проходит через точку O1 (рис. 13). Реакция T направлена по нити CD. Так как на цилиндр A действуют три силы, то на основании теоремы о трёх силах их линии действия должны пересекаться в точке O1. Следовательно, цилиндр A при равновесии займёт такое положение, при котором нить CD будет продолжением его радиуса.
Построим силовой треугольник (рис. 14). Этот треугольник подобен треугольнику OO1C . Из подобия треугольников
Или
Откуда

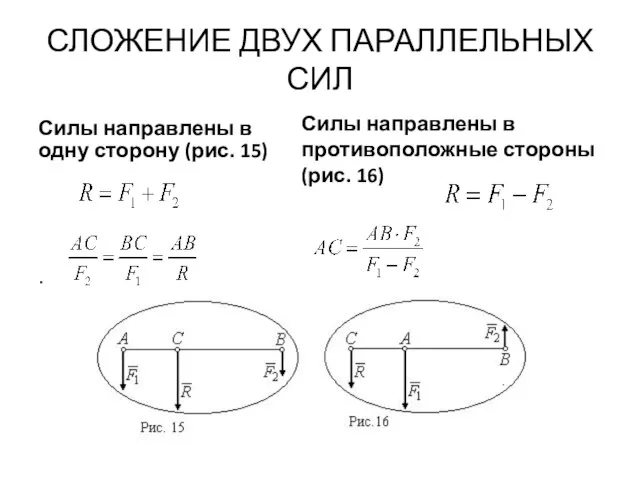
СЛОЖЕНИЕ ДВУХ ПАРАЛЛЕЛЬНЫХ СИЛ
Силы направлены в одну сторону (рис. 15)
.
Силы направлены в противоположные стороны (рис. 16)

ПАРА СИЛ
.
.
Пара сил - система двух равных по модулю, параллельных и противоположно направленных сил (рис. 17).
Плоскость действия пары сил – плоскость, в которой находятся линии действия сил.
Пара сил не имеет равнодействующей, однако силы пары не уравновешиваются, так как они не направлены по одной прямой. Пара стремится произвести вращение твёрдого тела, к которому она приложена.
Пара сил, не имея равнодействующей, очевидно, не может быть уравновешена силой.
Плечо пары сил – кратчайшее расстояние между линиями действия сил пары.
Действие пары сил на твёрдое тело характеризуется её моментом.
Момент пары сил – произведение одной из сил пары на её плечо.
M=Fd.

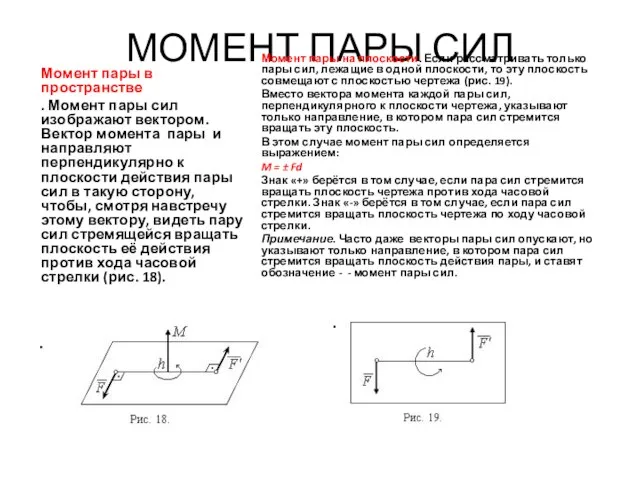
МОМЕНТ ПАРЫ СИЛ
Момент пары в пространстве
. Момент пары сил изображают вектором. Вектор момента пары и направляют перпендикулярно к плоскости действия пары сил в такую сторону, чтобы, смотря навстречу этому вектору, видеть пару сил стремящейся вращать плоскость её действия против хода часовой стрелки (рис. 18).
.
Момент пары на плоскости. Если рассматривать только пары сил, лежащие в одной плоскости, то эту плоскость совмещают с плоскостью чертежа (рис. 19).
Вместо вектора момента каждой пары сил, перпендикулярного к плоскости чертежа, указывают только направление, в котором пара сил стремится вращать эту плоскость.
В этом случае момент пары сил определяется выражением:
M = ± Fd
Знак «+» берётся в том случае, если пара сил стремится вращать плоскость чертежа против хода часовой стрелки. Знак «-» берётся в том случае, если пара сил стремится вращать плоскость чертежа по ходу часовой стрелки.
Примечание. Часто даже векторы пары сил опускают, но указывают только направление, в котором пара сил стремится вращать плоскость действия пары, и ставят обозначение - - момент пары сил.
.

ТЕОРЕМЫ О ПАРАХ
Теорема 1 . Две пары сил лежащие в одной плоскости, эквивалентны, если равны их алгебраические моменты.
Следствие: Пару сил можно перемещать в плоскости её действия.
Теорема 2 . Пару сил можно перемещать в любую плоскость, параллельную плоскости её действия.
Следствие теорем 1 и 2: Вектор момента пары сил – свободный вектор, т.е. его можно перемещать параллельно самому себе в любую точку тела.
Примечание1: следствия теорем 1 и 2 справедливы только для твёрдого тела и не справедливы для деформируемого тела, так как деформация тела зависит от места приложения пары сил.

ТРЕТЬЯ ТЕОРЕМА О ПАРАХ
Теорема 3 . Две пары сил можно заменять одной эквивалентной парой, момент которой равен геометрической сумме векторов моментов исходных пар.
Следствие 1: Любая система пар сил приводится к одной равнодействующей паре, момент которой равен геометрической сумме векторов моментов исходных пар.
Следствие 2 : Для равновесия системы пар, действующих на твёрдое тело, необходимо и достаточно, чтобы сумма моментов пар равнялась нулю, т.е. условие равновесия систем пар выглядит так:
- в случае пространственной системы пар:
- в случае системы пар, расположенных в одной плоскости :
Примечание: момент пары является математической моделью. Вектор момента пары аналогичен вектору момента силы, но имеет существенное отличие. Вектор момента пары является свободным вектором, т.е. его можно перемещать относительно твёрдого тела, не изменяя состояния тела.

Момент силы
относительно точки на плоскости
.
.
. Линия действия силы - это прямая, вдоль которой направлен вектор силы.
Плечо силы относительно точки - есть длина перпендикуляра, опущенного из точки на линию действия силы (рис. 20).
Выражение
читается - момент силы относительно точки А.

АЛГЕБРАИЧЕСКИЙ МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ
Пример 1
Пример 2
Алгебраический момент силы относительно точки - скалярная величина , равная произведению модуля силы на плечо, взятому со знаком плюс или минус. Знак плюс берут, когда сила вращает плечо вокруг точки против хода часовой стрелки и знак минус – по ходу часовой стрелки.

МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ в пространстве
.
(векторная величина)
Момент силы относительно точки изображается вектором , который перпендикулярен к плоскости, содержащей силу и точку, и направлен так, что, глядя навстречу вектору , видим силу , стремящейся вращать эту плоскость против хода часовой стрелки (рис. 23).
Модуль этого вектора равен произведению модуля силы на плечо относительно точки :
Плечо является кратчайшим расстоянием от этой точки до линии действия силы (длиной перпендикуляра, опущенного из точки на линию действия силы).
Модуль момента силы относительно точки может быть выражен удвоенной площадью треугольника .
Момент силы относительно точки равен нулю в том случае, если линия действия силы проходит через эту точку, т.е. . Если из точки в точку приложения силы провести радиус-вектор , то вектор момента силы выражается векторным произведением:

МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ
.
.
Правило определения момента силы относительно оси (например z). Чтобы вычислить момент этой силы относительно оси z (обозначается ) необходимо выполнить следующее (рис. 24):
Провести плоскость s перпендикулярно оси . Точка O - точка встречи оси z с плоскостью s.
Спроектировать силу F на плоскость - получается проекция Fι.
Момент силы F относительно оси z равен моменту проекции Fι относительно точки , т.е.
Момент силы относительно оси считается положительным, если, глядя навстречу оси z, можно видеть проекцию стремящейся вращать плоскость вокруг оси против хода часовой стрелки.

АНАЛИТИЧЕСКИЕ ВЫРАЖЕНИЯ МОМЕНТА
.

Аналитические выражения момента Продолжение
.

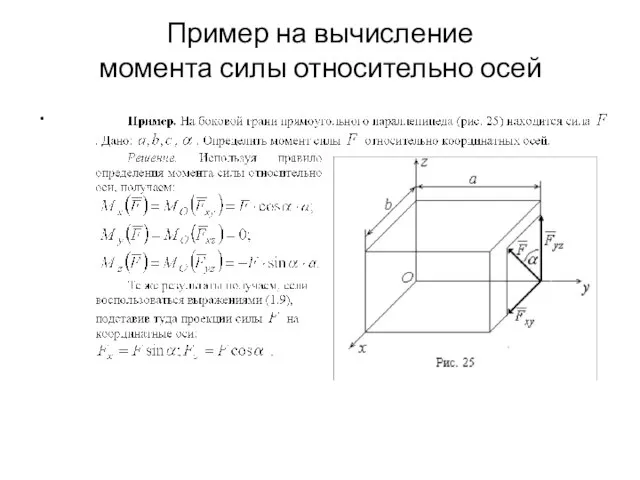
Пример на вычисление
момента силы относительно осей
.

ЛЕММА ПУАНСО
(лемма о параллельном переносе силы)
.

Основная теорема статики
(теорема Пуансо)
.

ОСНОВНАЯ ТЕОРЕМА СТАТИКИ
(доказательство)
.

УСЛОВИЯ РАВНОВЕСИЯ
ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ
.

УСЛОВИЯ РАВНОВЕСИЯ
СИСТЕМЫ ПАРАЛЛЕЛЬНЫХ СИЛ
.

УСЛОВИЯ РАВНОВЕСИЯ ПРОИЗВОЛЬНОЙ ПЛОСКОЙ СИСТЕМЫ СИЛ
.

ПЛОСКАЯ СИСТЕМА СИЛ
ТРИ ФОРМЫ УСЛОВИЙ РАВНОВЕСИЯ
.

ЦЕНТР ТЯЖЕСТИ
.

ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ
.

ОПРЕДЕЛЕНИЕ КООРДИНАТ ЦЕНТРА ПАРАЛЛЕЛЬНЫХ СИЛ
.

КООРДИНАТЫ ЦЕНТРА ТЯЖЕСТИ
.

СЦЕПЛЕНИЕ И ТРЕНИЕ СКОЛЬЖЕНИЯ
.

РАВНОВЕСИЕ СИСТЕМЫ ТЕЛ
.

РАВНОВЕСИЕ СИСТЕМЫ ТЕЛ
(продолжение)
.

СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ СИСТЕМЫ
Статически определимые системы – это такие системы тел, в которых число уравнений равно числу неизвестных сил. Если это условие не выполняется, то анализируют всю модель и приводят её к рассчитываемому виду, изменяя, как правило, внутренние связи механической системы.

КОНТРОЛЬНЫЕ ВОПРОСЫ ПО СТАТИКЕ
1. Назовите основные модели реальных тел в теоретической механике.
2. Сформулируйте аксиомы статики.
3. Что называется моментом силы относительно точки?
4. Перечислите элементарные операции над силами.
5. Какие системы сил называются эквивалентными?
6. Напишите общие условия равновесия твёрдого тела.
7. Что называется плоской системой сил?
8. Напишите условия равновесия плоской системы сил.
9. Какое твёрдое тело называется несвободным?
10. В каком случае три силы уравновешивают твёрдое тело?
11. Как выглядят условия равновесия тела с одной неподвижной точкой?
12. Напишите уравнения равновесия тела, способного вращаться вокруг неподвижной оси.
13. Назовите виды опор в схемах.
14. Чем отличаются шарнирно подвижная и шарнирно неподвижная опоры?
15. Какие уравнения являются наиболее удобными для нахождения реакций в брусе?

Соколов А.П.
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
(часть 2)
для студентов ЭНИН
направления 140100
ТЕПЛОЭНЕРГЕТИКА

КИНЕМАТИКА
Кинематика – раздел теоретической механики, в котором изучается движение тел без учёта действующих сил, т.е. движение с геометрической точки зрения.
Кинематикой называется та часть механики, в которой изучаются зависимости между величинами, характеризующими состояние систем, но не рассматриваются причины вызывающие изменение состояние движения.

КИНЕМАТИКА ТОЧКИ
Декартовы координаты.
С неподвижной системой отсчёта связываем декартовую ортогональную систему координат (правую, рис. 38).
Точка
, где
Рис.38

ТРАЕКТОРИЯ ТОЧКИ
.

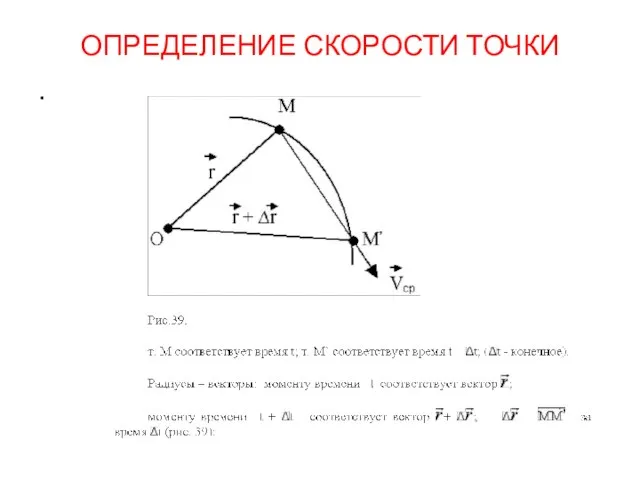
ОПРЕДЕЛЕНИЕ СКОРОСТИ ТОЧКИ
.

ОПРЕДЕЛЕНИЕ СКОРОСТИ
(продолжение)
.

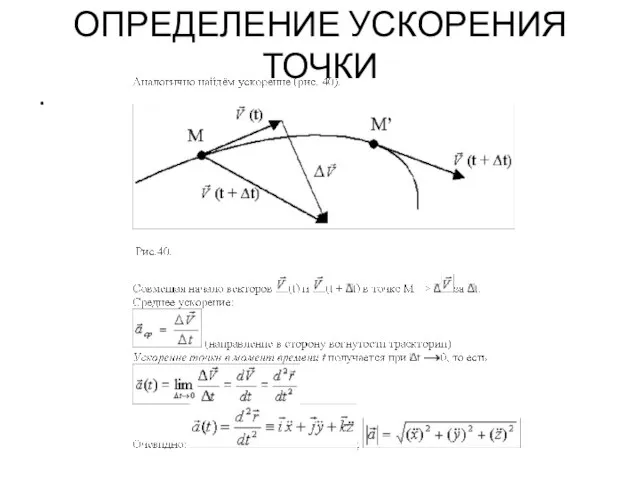
ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ ТОЧКИ
.

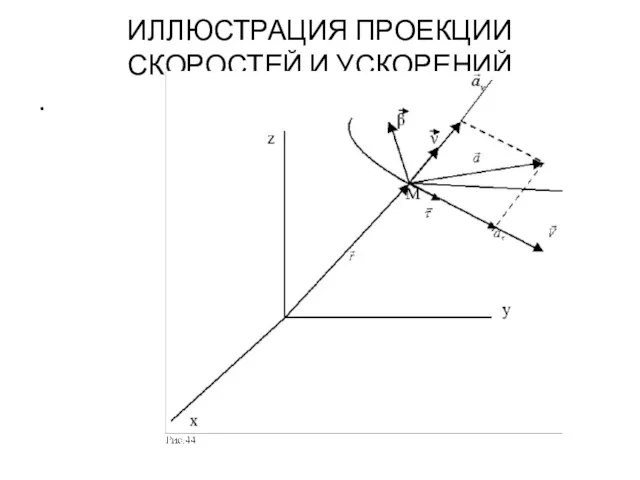
УСКОРЕНИЕ ТОЧКИ
(продолжение)
.

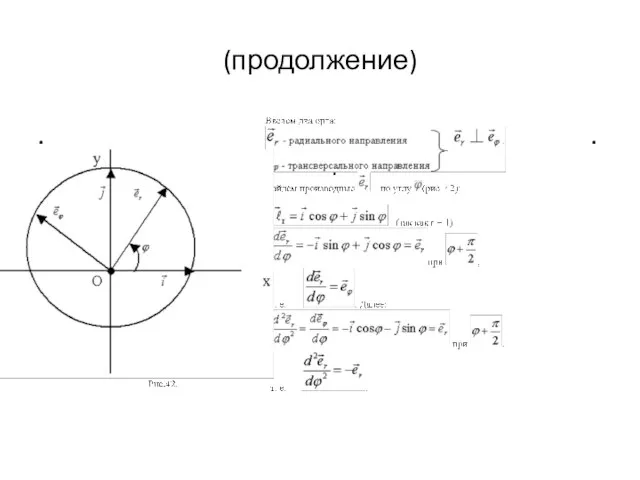
ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ В ПОЛЯРНЫХ КООРДИНАТАХ
.

(продолжение)
.
.
.
.

ОКОНЧАНИЕ
Проекции скорости:
Проекции ускорения:

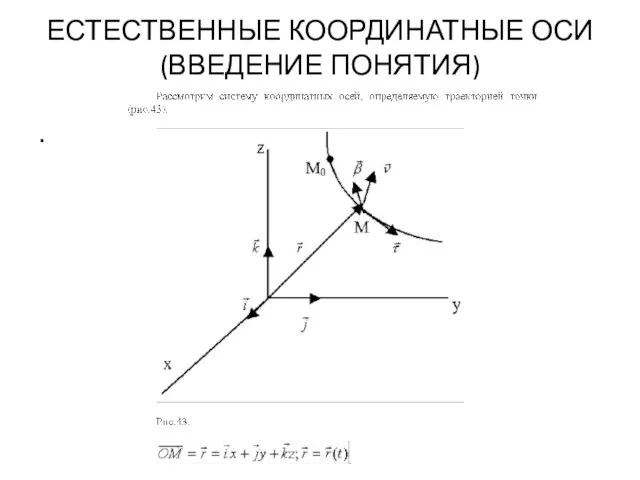
ЕСТЕСТВЕННЫЕ КООРДИНАТНЫЕ ОСИ
(ВВЕДЕНИЕ ПОНЯТИЯ)
.

ЕСТЕСТВЕННЫЕ КООРДИНАТНЫЕ ОСИ
.

ПРОЕКЦИИ СКОРОСТИ
НА ЕСТЕСТВЕННЫЕ ОСИ
.

ПРОЕКЦИЯ УСКОРЕНИЯ
НА ЕСТЕСТВЕННЫЕ ОСИ
.

ИЛЛЮСТРАЦИЯ ПРОЕКЦИИ СКОРОСТЕЙ И УСКОРЕНИЙ
.

Задача
.

КИНЕМАТИКА ТЕЛА
.

ВЗАИМОСВЯЗЬ ПОДВИЖНЫХ И НЕПОДВИЖНЫХ ОСЕЙ
.

ДОКАЗАТЕЛЬСТВО НЕОБХОДИМОСТИ ШЕСТИ НЕЗАВИСИМЫХ КООРДИНАТ ДЛЯ СВОБОДНОГО ТВЁРДОГО ТЕЛА
.

ДОКАЗАТЕЛЬСТВО НЕОБХОДИМОСТИ ШЕСТИ НЕЗАВИСИМЫХ КООРДИНАТ ДЛЯ СВОБОДНОГО ТВЁРДОГО ТЕЛА (окончание)
.

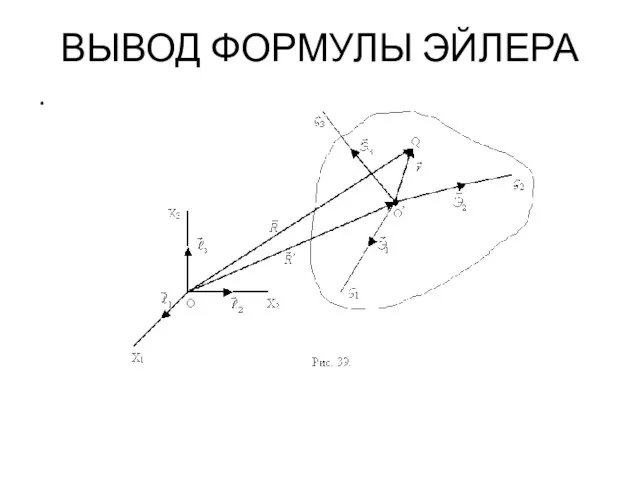
ВЫВОД ФОРМУЛЫ ЭЙЛЕРА
.

ПЕРЕХОД К АБСОЛЮТНОЙ СКОРОСТИ
.

ФОРМА РАСПРЕДЕЛЕНИЯ СКОРОСТЕЙ
.

Учёт свойств симметрии уравнений
.

Учёт движения относительно полюса
.

Учёт угловых скоростей движения тела
.

ФОРМУЛА ЭЙЛЕРА В ВЕКТОРНОЙ ЗАПИСИ
.

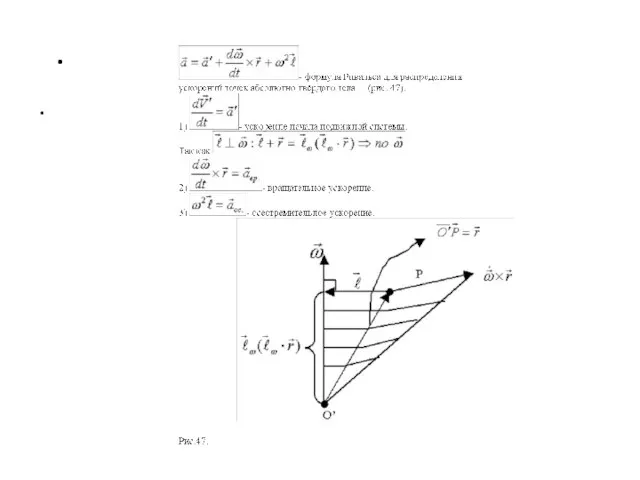
НАХОЖДЕНИЕ РАСПРЕДЕЛЕНИЯ УСКОРЕНИЙ
.

.
.

ЧАСТНЫЕ СЛУЧАИ ДВИЖЕНИЯ ТЕЛА
.

ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ О СКОРОСТЯХ ТОЧЕК ПРИ ПОСТУПАТЕЛЬНОМ ДВИЖЕНИИ
.

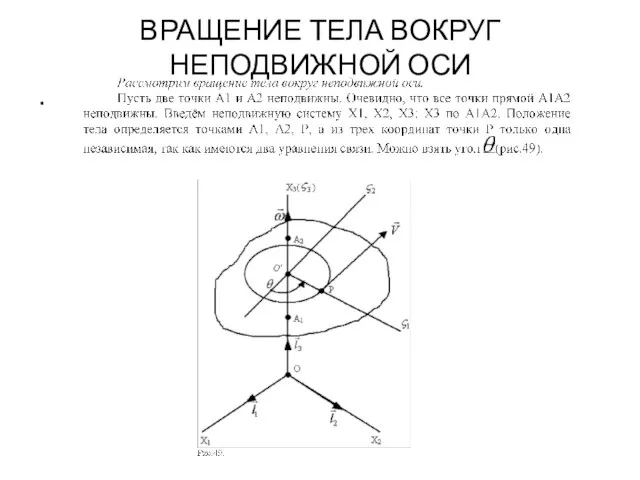
ВРАЩЕНИЕ ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
.

Нахождение скоростей и ускорений при вращательном движении
.

Распределение скоростей и ускорений при вращательном движении
.

ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ
.

ИЛЛЮСТРАЦИЯ ПЛОСКОПАРАЛЛЕЛЬНОГО ДВИЖЕНИЯ
.

АНАЛИТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ МЦС
.

АНАЛИТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ МЦС
(продолжение)
.

ПРИМЕР ОПРЕДЕЛЕНИЯ МЦС
.

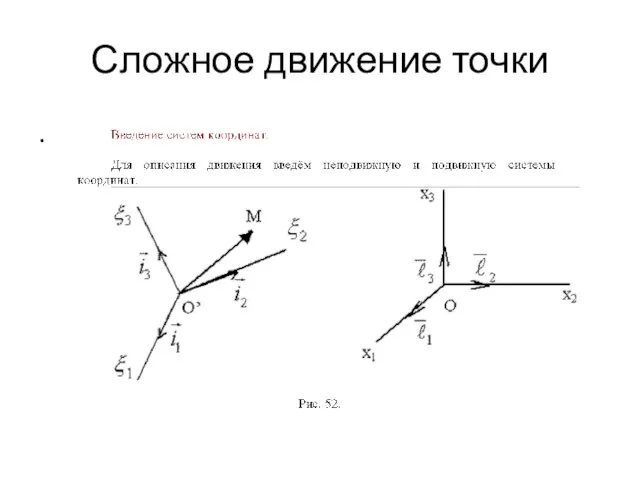
Сложное движение точки
.

Движение в подвижной системе координат
.

Определение относительной скорости

Определение абсолютной скорости
.

ОПРЕДЕЛЕНИЕ АБСОЛЮТНОГО УСКОРЕНИЯ
.

Формула Кориолиса
.

Соколов А.П.
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
(часть 3)
для студентов ЭНИН
направления 140100
ТЕПЛОЭНЕРГЕТИКА

ДИНАМИКА ТОЧКИ
.

Меры
движения
.

Кинетическая энергия материальной точки
.

ЗАКОНЫ НЬЮТОНА
.

ТРЕТИЙ ЗАКОН НЬЮТОНА
.

ПРИНЦИП СУПЕРПОЗИЦИИ
.

ИДЕАЛИЗАЦИЯ СИЛ
.

ЗАДАЧИ ДИНАМИКИ ТОЧКИ
.

ТЕОРЕМА ОБ ИЗМЕНЕНИИ
МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ
.

Теорема об изменении кинетической энергии
.

ЗАКОНЫ СОХРАНЕНИЯ
.

С учётом потенциала силового поля
.

С учётом уравнения кинетической энергии в полных дифференциалах
.

ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
.

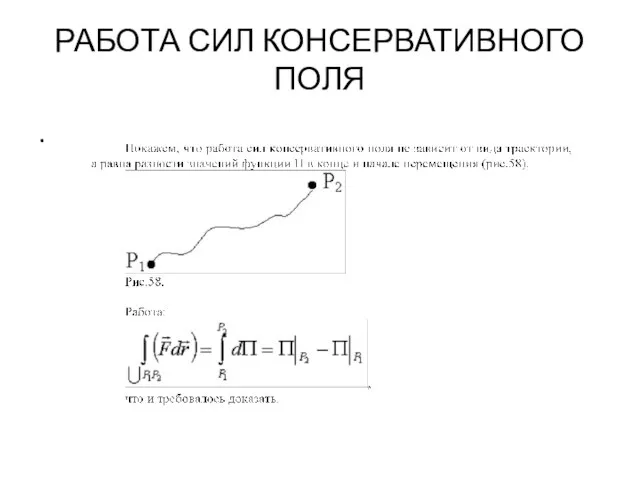
РАБОТА СИЛ КОНСЕРВАТИВНОГО ПОЛЯ
.

Работа сил консервативного поля на замкнутом перемещении
.

Решение уравнений движения для частных случаев силовых полей
.

.
.

.
.

ДИНАМИКА МЕХАНИЧЕСКОЙ СИСТЕМЫ
.

МАССОВЫЕ ХАРАКТЕРИСТИКИ СИСТЕМЫ
.

ОСНОВНЫЕ МЕРЫ ДВИЖЕНИЯ СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
.

Кинетический момент и кинетическая энергия системы
.

СИЛЫ ВНЕШНИЕ И ВНУТРЕННИЕ
.

СВОЙСТВА ВНУТРЕННИХ СИЛ
.

Сумма элементарных работ внутренних сил
.

Общие (основные) теоремы динамики системы
.

.
.

.
.

.
.

ЗАКОНЫ СОХРАНЕНИЯ
.

УРАВНЕНИЯ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
.

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
.

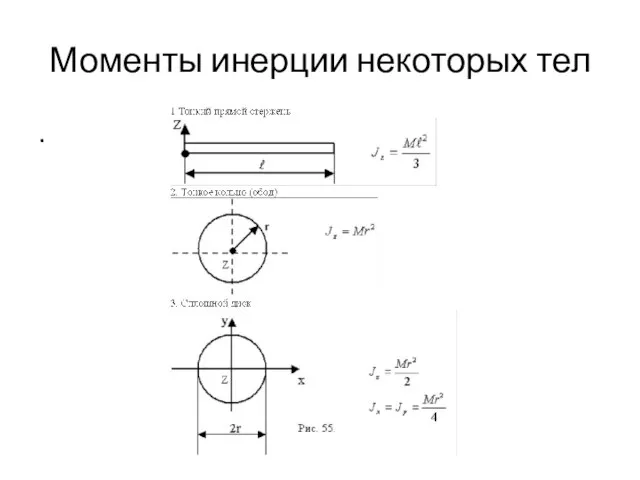
Моменты инерции некоторых тел
.

ПРИМЕР
.