Способы решений логических задач

Задача
Три свидетеля ограбления банка сообщили сведения о грабителе: цвет волос и особые приметы. Первый утверждает, что был брюнет в очках. Второй, сказал, что грабитель – шатен с бородой, а третий показал, что грабитель точно не брюнет и, по всей видимости был в шляпе. Когда удалось взять грабителя, выяснилось, что каждый из свидетелей точно определил только одну из примет грабителя, а в другой ошибся.
Ответ запишите в виде двух слов, разделенных пробелом: цвет волос примета.
Например: БЛОНДИН С УСАМИ.

средствами алгебры логики;
с помощью рассуждений;
табличный;
другие.
Способы решения задач

1. Средствами алгебры логики
Схема решения:
изучается условие задачи;
вводится система обозначений для логических высказываний;
конструируется логическая формула, описывающая логические связи между всеми высказываниями условия задачи;
определяются значения истинности этой логической формулы;
из полученных значений истинности формулы определяются значения истинности введённых логических высказываний, на основании которых делается заключение о решении.

Обозначим высказывания:
А=«грабитель брюнет»
В=«грабитель был в очках»
С=«грабитель шатен»
D=«грабитель с бородой»
Е=«грабитель был в шляпе»
Согласно условию:
Из показаний 1-го свидетеля следует, что истинно;
Из показаний 2-го свидетеля следует, что истинно;
Из показаний 3-го свидетеля следует, что истинно;
Следовательно, истинна и конъюнкция

Раскрывая скобки , получаем:
Из полученных восьми слагаемых семь (согласно условию являются ложными, остается единственное истинное слагаемое:

А=«грабитель брюнет»
В=«грабитель был в очках»
С=«грабитель шатен»
D=«грабитель с бородой»
Е=«грабитель был в шляпе»
Значит, грабитель - шатен в очках.
Ответ: шатен в очках.

2. Решение логических задач с помощью рассуждений
Этим способом обычно решают несложные логические задачи.
Предположим, что первый свидетель правильно сообщил, что грабитель был брюнет, но ошибся в том, что тот бы в очках. Следовательно, грабитель брюнет, но не в очках. Тогда неверны оба утверждения второго свидетеля, что противоречит условию задачи. Следовательно, первый свидетель правильно сообщил, что грабитель был в очках, но не брюнет. Тогда из показаний третьего свидетеля- грабитель в шляпе – неверно. А из показаний второго свидетеля следует, что грабитель - шатен в очках.
.

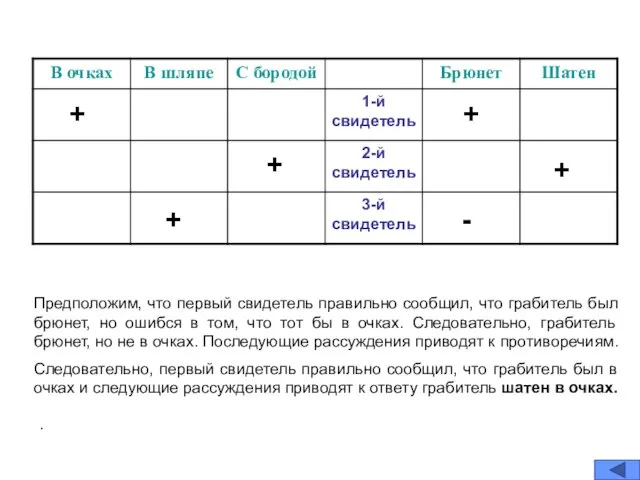
Предположим, что первый свидетель правильно сообщил, что грабитель был брюнет, но ошибся в том, что тот бы в очках. Следовательно, грабитель брюнет, но не в очках. Последующие рассуждения приводят к противоречиям.
Следовательно, первый свидетель правильно сообщил, что грабитель был в очках и следующие рассуждения приводят к ответу грабитель шатен в очках.
+
+
+
+
+
-
.

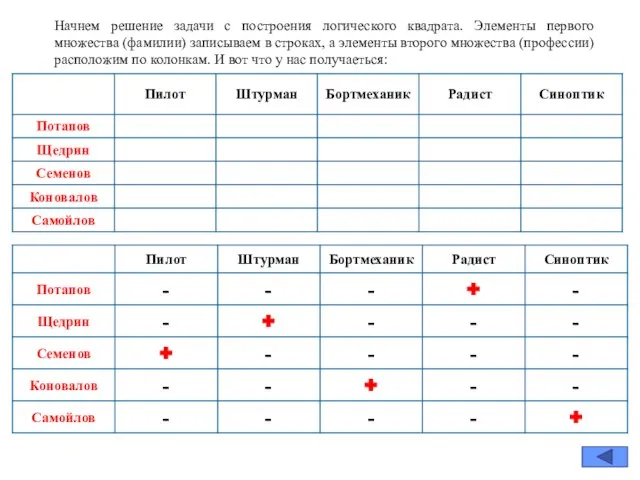
В авиационном подразделении служат Потапов, Щедрин, Семенов, Коновалов и Самойлов. Их специальности (они перечислены не в том же порядке, что и фамилии): пилот, штурман, бортмеханик, радист и синоптик. Об этих людях известно следующее:
1. Щедрин и Коновалов не умеют управлять самолетом.
2. Потапов и Коновалов готовятся стать штурманами.
3. Щедрин и Самойлов живут в одном доме с радистом.
4. Семенов был в доме отдыха вместе со Щедриным и сыном синоптика.
5. Потапов и Щедрин в свободное время любят играть в шахматы с бортмехаником.
6. Коновалов, Семенов и синоптик увлекаются боксом.
7. Радист боксом не увлекается.
Задача-2

3. Решение данной задачи табличным способом
При использовании этого способа условия, которые содержит задача, и результаты рассуждений фиксируются с помощью специально составленных таблиц.

Начнем решение задачи с построения логического квадрата. Элементы первого множества (фамилии) записываем в строках, а элементы второго множества (профессии) расположим по колонкам. И вот что у нас получаеться: