Работу выполнили учащиеся 8 класса Фирсова Маргарита и Колупаева Ольга под руководством учителя Васильевой Т. Г.

О теореме Пифагора написано огромное количество научной литературы. В ней присутствуют, в основном, современные доказательства.

Проблема:
Как возникла теорема Пифагора?

Цель:
изучить эпоху возникновения теоремы Пифагора и способы её доказательства

Задачи:
1.Выяснить историю возникновения теоремы.
2.Изучить разные способы доказательства теоремы.

Гипотеза
Мы думаем, что теорема Пифагора возникла прежде всего из практических нужд, когда ученые древности наблюдали за различными построениями на земле.

Еще в древности возникла необходимость вычислять стороны прямоугольных треугольников по двум известным сторонам. Построение прямых углов египтянами. Нахождение высоты объекта и определение расстояния до недоступного предмета.
Такие задачи решаются
и в нашей повседневной жизни

Пифагор – великий математик
Обычно открытие теоремы Пифагора приписывают древнегреческому философу и математику Пифагору (VI в до н. э.).
Но изучение вавилонских клинописных таблиц и древнекитайских рукописей показало, что утверждение было известно задолго до Пифагора.

Взгляды Кантора
Кантор (крупнейший немецкий историк математики) считает, что равенство 32 +42 = 52 было известно уже египтянам ещё около 2300 г до н.э.
По мнению Кантора, гарпедонапты, или «натягиватели веревок» строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5

Взгляды вавилонян
Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте, относимом ко времени Хаммураби, т. е. к 2000 г. до н. э., приводится приближенное вычисление гипотенузы прямоугольного треугольника. Отсюда можно сделать вывод, что в Двуречье умели производить вычисления с прямоугольными треугольниками, по крайней мере в некоторых случаях. Основываясь, с одной стороны, на сегодняшнем уровне знаний о египетской и вавилонской математике, а с другой-на критическом изучении греческих источников, Ван-дер-Варден (голландский математик) сделал следующий вывод:

"Заслугой первых греческих математиков, таких как Фалес, Пифагор и пифагорейцы, является не открытие математики, но ее систематизация и обоснование. В их руках вычислительные рецепты, основанные на смутных представлениях, превратились в точную науку."

Доказательство для равнобедренных треугольников
Достаточно взглянуть на мозаику из черных и светлых треугольников, изображенную на рисунке, чтобы убедиться в справедливости теоремы для треугольника АВС: квадрат построенный на гипотенузе, содержит 4 треугольника, а на каждом катете построен квадрат, содержащий 2 треугольника.

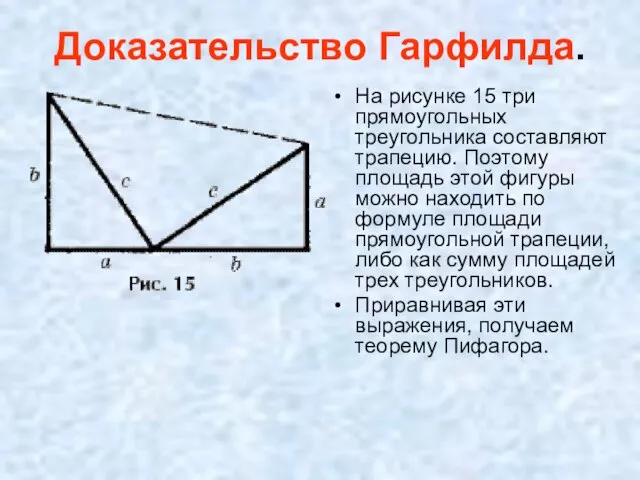
Доказательство Гарфилда.
На рисунке 15 три прямоугольных треугольника составляют трапецию. Поэтому площадь этой фигуры можно находить по формуле площади прямоугольной трапеции, либо как сумму площадей трех треугольников.
Приравнивая эти выражения, получаем теорему Пифагора.

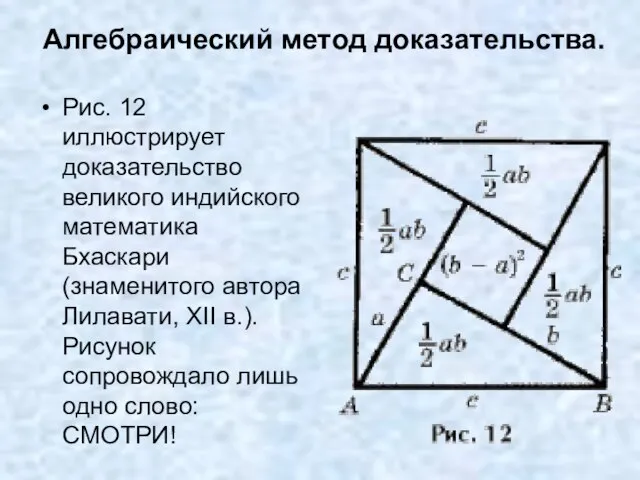
Алгебраический метод доказательства.
Рис. 12 иллюстрирует доказательство великого индийского математика Бхаскари (знаменитого автора Лилавати, XII в.). Рисунок сопровождало лишь одно слово: СМОТРИ!

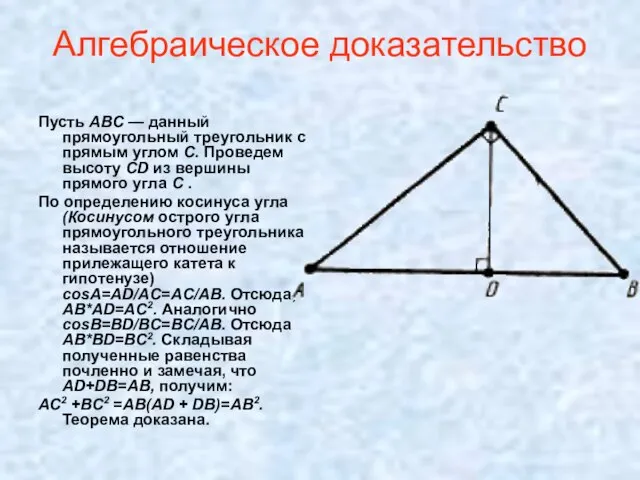
Алгебраический метод
На рис. 13 ABC – прямоугольный треугольник, C – прямой угол, AB - гипотенуза, b1 – проекция катета b на гипотенузу, a1 – проекция катета a на гипотенузу, h – высота треугольника, проведенная к гипотенузе.
Из того, что ABC подобен ACM следует ; (1)
из того, что ABC подобен BCM следует 2)
Складывая почленно равенства (1) и (2), получим

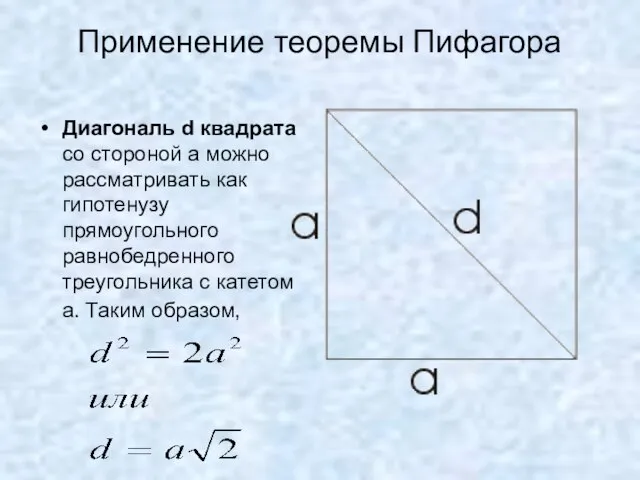
Применение теоремы Пифагора
Диагональ d квадрата со стороной а можно рассматривать как гипотенузу прямоугольного равнобедренного треугольника с катетом а. Таким образом,

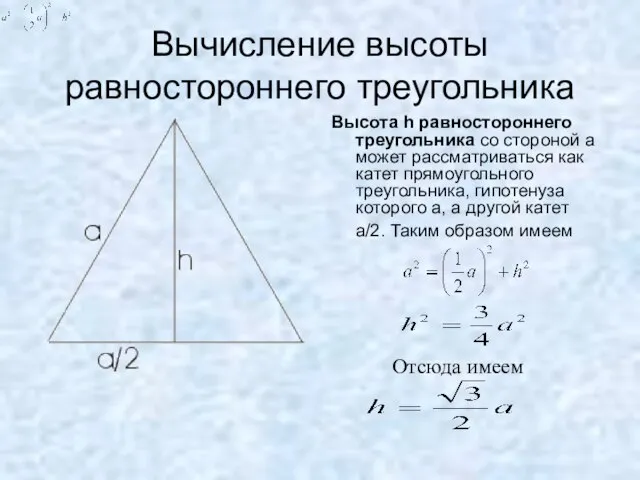
Вычисление высоты равностороннего треугольника
Высота h равностороннего треугольника со стороной а может рассматриваться как катет прямоугольного треугольника, гипотенуза которого а, а другой катет a/2. Таким образом имеем
Отсюда имеем

З а к л ю ч е н и е
Если дан нам
треугольник
И притом с прямым углом
То квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим.
И таким простым путем
К результату мы придем.

Спасибо
за внимание

Используемая литература:
1. Геометрия: учебн. для 7-9 кл. средн. школы авт. Л. С. Атанасян
2. Геометрия: учебн. для 10-11 кл. средн. школы авт. Л. С. Атанасян
3. Энциклопедический словарь юного математика.
Авт. А. П. Савин.
4. Энциклопедия для детей. Глав. ред. М. Д. Аксенова
5. Волошина А.В. Математика и искусство. М.,Просвещение,1992
6. Волошина А.В. Пифагор.,1992
7. Глейзер Г.И. История математики в школе.М.,1982
8. Литцман В. Теорема Пифагора.М.,1960

Алгебраическое доказательство
Пусть АВС — данный прямоугольный треугольник с прямым углом С. Проведем высоту CD из вершины прямого угла С .
По определению косинуса угла (Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе) соsА=AD/AC=AC/AB. Отсюда, AB*AD=AC2. Аналогично соsВ=BD/BC=BC/AB. Отсюда AB*BD=ВС2. Складывая полученные равенства почленно и замечая, что AD+DB=AB, получим:
АС2 +ВС2 =АВ(AD + DB)=АВ2. Теорема доказана.

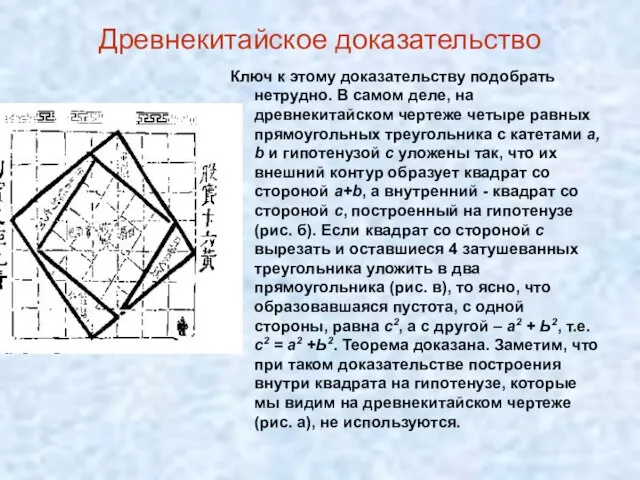
Древнекитайское доказательство
Ключ к этому доказательству подобрать нетрудно. В самом деле, на древнекитайском чертеже четыре равных прямоугольных треугольника с катетами а, b и гипотенузой с уложены так, что их внешний контур образует квадрат со стороной а+b, а внутренний - квадрат со стороной с, построенный на гипотенузе (рис. б). Если квадрат со стороной с вырезать и оставшиеся 4 затушеванных треугольника уложить в два прямоугольника (рис. в), то ясно, что образовавшаяся пустота, с одной стороны, равна с2, а с другой – а2 + Ь2, т.е. с2 = а2 +Ь2. Теорема доказана. Заметим, что при таком доказательстве построения внутри квадрата на гипотенузе, которые мы видим на древнекитайском чертеже (рис. а), не используются.