Содержание
- 2. Цель работы Целью данной работы было достижение максимальной эффективности при распараллеливании данного класса задач. Две парадигмы
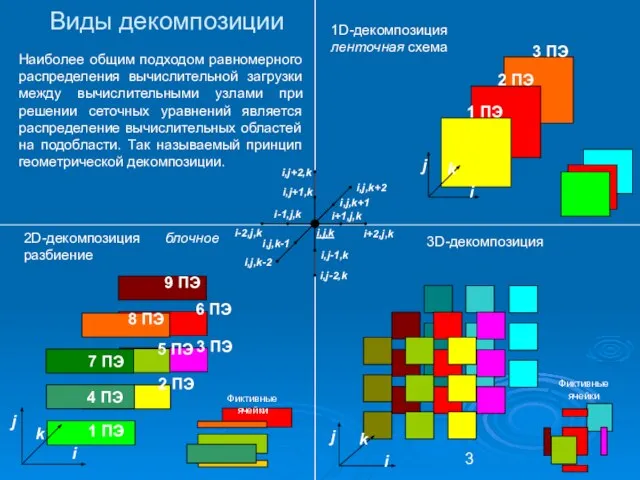
- 3. 1D-декомпозиция ленточная схема 2D-декомпозиция блочное разбиение 3D-декомпозиция Виды декомпозиции Наиболее общим подходом равномерного распределения вычислительной загрузки
- 4. Математическая постановка Требуется решить трехмерное уравнение переноса в единичном кубе с граничными условиями второго рода и
- 5. Аппроксимация Аппроксимация дифференциальной задачи осуществляется на основе метода конечного объема. Аппроксимация конвективных членов уравнений переноса выполняется
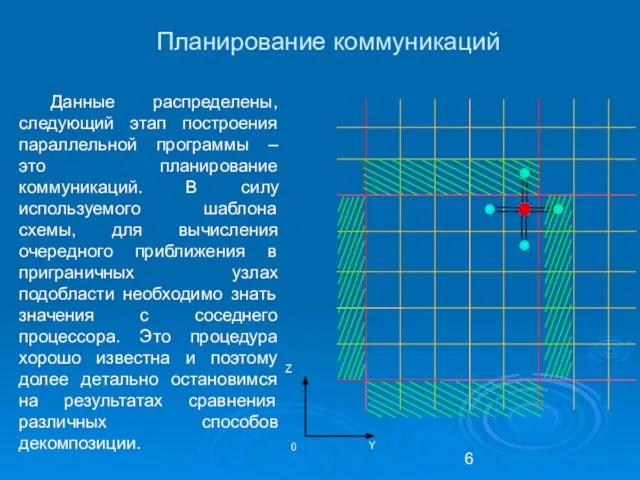
- 6. Данные распределены, следующий этап построения параллельной программы – это планирование коммуникаций. В силу используемого шаблона схемы,
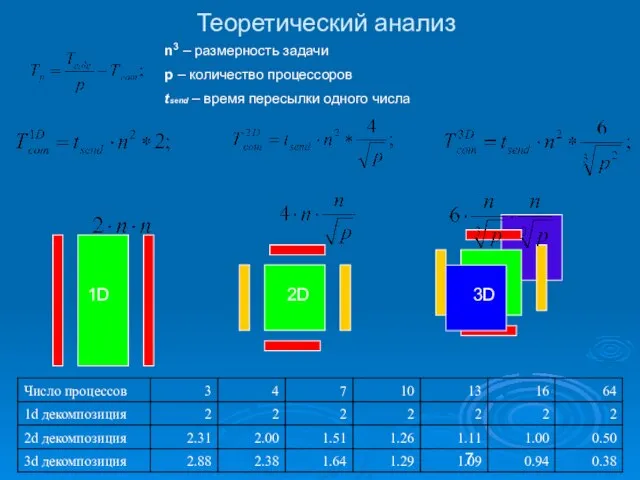
- 7. Теоретический анализ n3 – размерность задачи p – количество процессоров tsend – время пересылки одного числа
- 8. Вычислительный кластер имеет 283 вычислительных узла, один узел включает два двухъядерных процессора Intel 5150, 2,66ГГц, 4
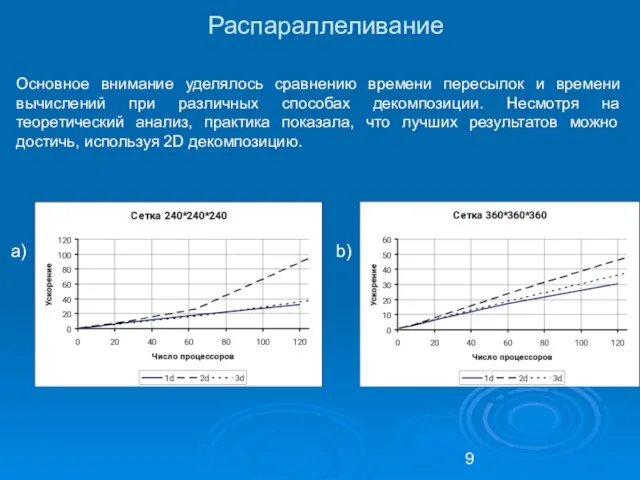
- 9. Распараллеливание Основное внимание уделялось сравнению времени пересылок и времени вычислений при различных способах декомпозиции. Несмотря на
- 10. Для оценки состоятельности первого допущения был рассмотрен случай, когда программа запускалась в однопроцессорном варианте, и при
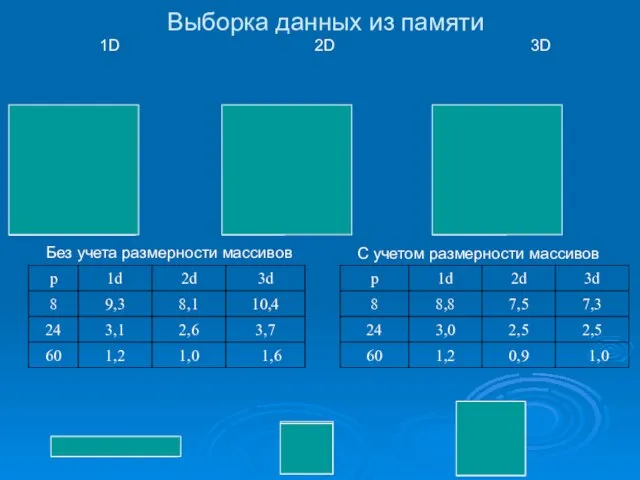
- 11. Выборка данных из памяти Без учета размерности массивов C учетом размерности массивов 1D 2D 3D
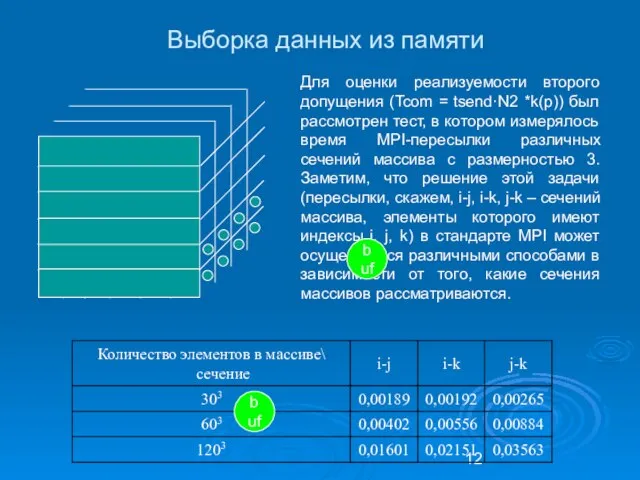
- 12. Для оценки реализуемости второго допущения (Tcom = tsend·N2 *k(p)) был рассмотрен тест, в котором измерялось время
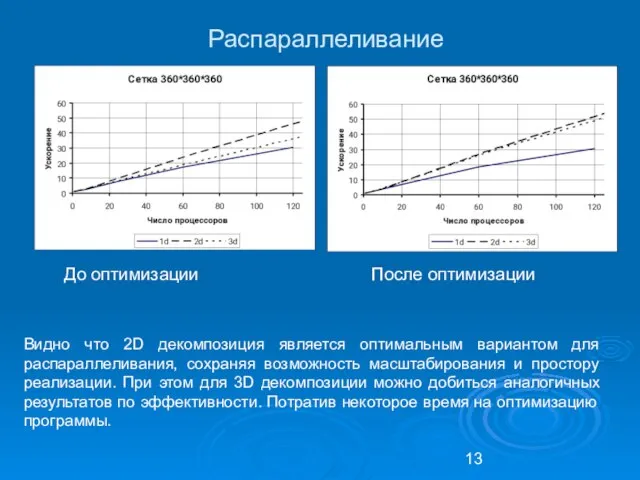
- 13. Распараллеливание Видно что 2D декомпозиция является оптимальным вариантом для распараллеливания, сохраняя возможность масштабирования и простору реализации.
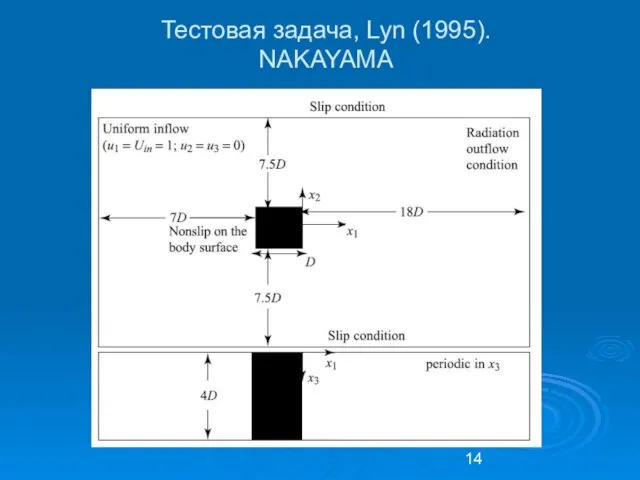
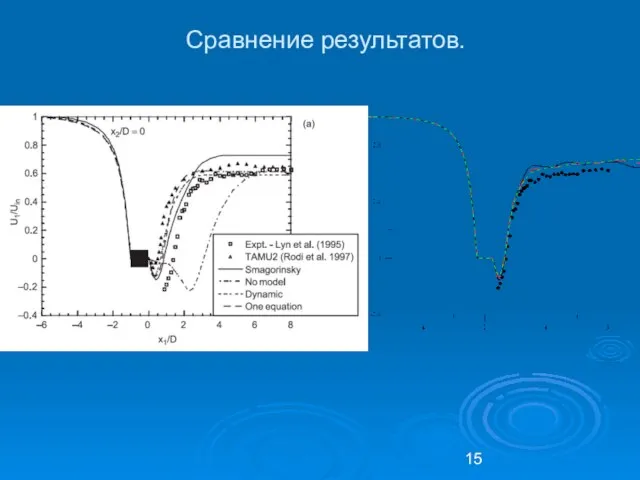
- 14. Тестовая задача, Lyn (1995). NAKAYAMA
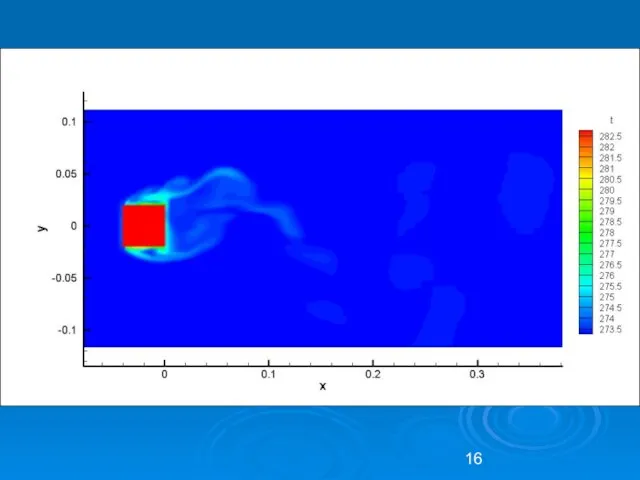
- 15. Сравнение результатов.
- 18. Скачать презентацию





 THE CHRISTIAN WORKER
THE CHRISTIAN WORKER 1665678763032__30ro86
1665678763032__30ro86 Агрессия (4 класс)
Агрессия (4 класс) 1.1 + 1.2
1.1 + 1.2 История носового платка
История носового платка Поля листа
Поля листа Вкусное и красивое лакомство для неожиданных гостей
Вкусное и красивое лакомство для неожиданных гостей Добро пожаловать
Добро пожаловать Независимое распределение затрат в управленческом и регламентированном учете
Независимое распределение затрат в управленческом и регламентированном учете Абсолютные показатели оценки риска
Абсолютные показатели оценки риска Кипение
Кипение Страны Северной Европы
Страны Северной Европы Конструкция головы человека и её пропорции (6 класс)
Конструкция головы человека и её пропорции (6 класс) Энтеровирусная инфекция
Энтеровирусная инфекция Конвекция
Конвекция САНИТАРНО-ЭПИДЕМИОЛОГИЧЕСКИЕ ТРЕБОВАНИЯ К УСЛОВИЯМИ ОРГАНИЗАЦИИ ОБУЧЕНИЯ В ОБЩЕОБРАЗОВАТЕЛЬНЫХ УЧРЕЖДЕНИЯХ
САНИТАРНО-ЭПИДЕМИОЛОГИЧЕСКИЕ ТРЕБОВАНИЯ К УСЛОВИЯМИ ОРГАНИЗАЦИИ ОБУЧЕНИЯ В ОБЩЕОБРАЗОВАТЕЛЬНЫХ УЧРЕЖДЕНИЯХ Ассоциация «МЫ»
Ассоциация «МЫ»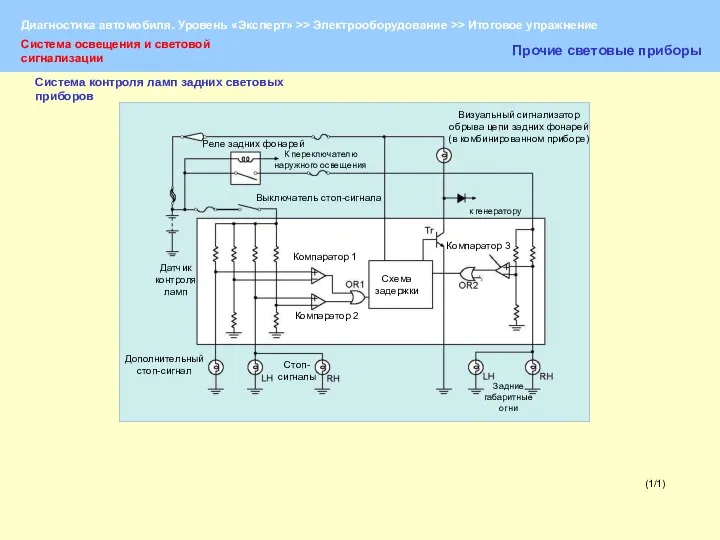 Диагностика автомобиля. Диагностирование осветительных приборов
Диагностика автомобиля. Диагностирование осветительных приборов Денис Васильевич Давыдов
Денис Васильевич Давыдов Рекомендую как пособие по медицинской генетике
Рекомендую как пособие по медицинской генетике Любимый семейный завтрак семьи Пьянковых
Любимый семейный завтрак семьи Пьянковых Доброта
Доброта О РЕЗУЛЬТАТАХ ЕГЭ в г. Сочи в 2011 ГОДУ
О РЕЗУЛЬТАТАХ ЕГЭ в г. Сочи в 2011 ГОДУ Психологические закономерности формирования личности в тренировочном процессе.
Психологические закономерности формирования личности в тренировочном процессе. Базовый межшкольный методический центр 26311
Базовый межшкольный методический центр 26311 Сложение и вычитание двузначных чисел 2 класс
Сложение и вычитание двузначных чисел 2 класс Выявление и устройство детей-сирот и детей оставшихся без попечения родителей.
Выявление и устройство детей-сирот и детей оставшихся без попечения родителей. Создание единого китайского государства
Создание единого китайского государства