Содержание
- 2. Статически определимой называется система, в которой для нахождения всех силовых факторов (реакций внешних и внутренних связей
- 3. РЕЗЮМЕ О СТАТИЧЕСКОЙ ОПРЕДЕЛИМОСТИ В строгом смысле, свойством статической определимости (или неопределимости) обладает не сама система,
- 4. Общие свойства статически определимых систем (СОС) 1. Все силовые факторы в статически определимой системе могут быть
- 5. ОСНОВНЫЕ ТИПЫ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ СИСТЕМ Многопролётные балки Фермы Арки Рамы Трёхшарнирные системы К о м б
- 6. МНОГОПРОЛЁТНЫЕ СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ БАЛКИ
- 7. Многопролётная балка – это геометрически неизменяемая система, состоящая из прямолинейных стержней – одного или нескольких, шарнирно
- 8. Основные структурные схемы многопролётных СО балок …ш-ш – о-о – ш-ш – о-о… …ш – о
- 9. Особенности работы МСОБ под нагрузками 1) нагрузка, приложенная к главной части, вызывает усилия (изгибающие моменты и
- 10. 1) нагрузка, приложенная к главной части, вызывает усилия (изгибающие моменты и поперечные силы) только в загруженной
- 11. Расчёт МСОБ на действие неподвижной (постоянной) нагрузки – п р и м е р ГЧ1 УГЧ2
- 12. Расчёт МСОБ на действие неподвижной (постоянной) нагрузки – п р и м е р ГЧ1 УГЧ2
- 13. Расчёт МСОБ на действие неподвижной (постоянной) нагрузки – п р и м е р ГЧ1 УГЧ2
- 14. Расчёт МСОБ на действие неподвижной (постоянной) нагрузки – п р и м е р ГЧ1 УГЧ2
- 15. Расчёт МСОБ на действие неподвижной (постоянной) нагрузки – п р и м е р ГЧ1 УГЧ2
- 16. Расчёт МСОБ на временные (подвижные) нагрузки с помощью линий влияния Построение линий влияния опорных реакций и
- 17. Расчёт МСОБ на временные (подвижные) нагрузки с помощью линий влияния Построение линий влияния опорных реакций и
- 18. Расчёт МСОБ на временные (подвижные) нагрузки с помощью линий влияния Построение линий влияния опорных реакций и
- 19. Расчёт МСОБ на временные (подвижные) нагрузки с помощью линий влияния Построение линий влияния опорных реакций и
- 20. Расчёт МСОБ на временные (подвижные) нагрузки с помощью линий влияния Построение линий влияния опорных реакций и
- 21. Расчёт МСОБ на временные (подвижные) нагрузки с помощью линий влияния Построение линий влияния опорных реакций и
- 22. Расчёт МСОБ на временные (подвижные) нагрузки с помощью линий влияния Построение линий влияния опорных реакций и
- 23. Расчёт МСОБ на временные (подвижные) нагрузки с помощью линий влияния Построение линий влияния опорных реакций и
- 24. Расчёт МСОБ на временные (подвижные) нагрузки с помощью линий влияния Построение линий влияния опорных реакций и
- 25. К о н т р о л ь н ы е в о п р о
- 27. Скачать презентацию
Слайд 2Статически определимой называется система,
в которой для нахождения всех силовых факторов
(реакций
Статически определимой называется система,
в которой для нахождения всех силовых факторов
(реакций
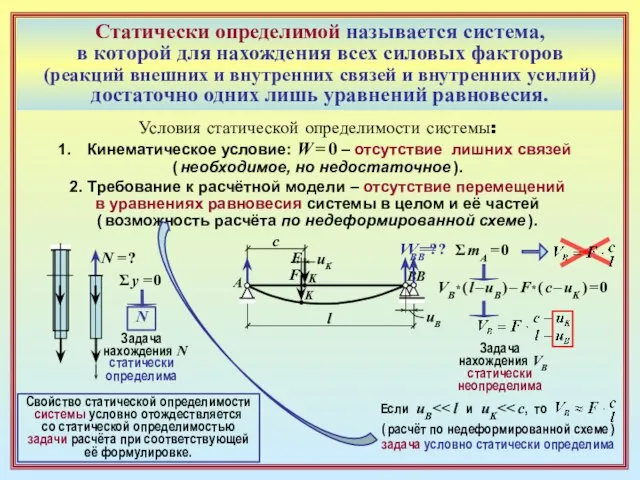
Условия статической определимости системы:
Кинематическое условие: W = 0 – отсутствие лишних связей
( необходимое, но недостаточное ).
2. Требование к расчётной модели – отсутствие перемещений
в уравнениях равновесия системы в целом и её частей
( возможность расчёта по недеформированной схеме ).
N = ?
l
Σ y = 0
N
Задача
нахождения N статически
определима
c
A
B
B
K
K
F
F
VB = ?
VB = ?
Σ mA = 0
uB
uK
VB* ( l – uB ) – F* ( c – uK ) = 0
Задача
нахождения VB статически
неопределима
Если uB<< l и uK<< c, то
( расчёт по недеформированной схеме )
задача условно статически определима
Свойство статической определимости
системы условно отождествляется
со статической определимостью
задачи расчёта при соответствующей
её формулировке.
Слайд 3РЕЗЮМЕ О СТАТИЧЕСКОЙ ОПРЕДЕЛИМОСТИ
В строгом смысле, свойством статической определимости
(или неопределимости) обладает
РЕЗЮМЕ О СТАТИЧЕСКОЙ ОПРЕДЕЛИМОСТИ
В строгом смысле, свойством статической определимости
(или неопределимости) обладает

а задача ее расчёта, сформулированная с использованием
тех или иных гипотез и предпосылок.
Но формально понятие «статическая определимость»
можно отнести к системе без лишних связей в случае,
когда в записанных для неё уравнениях равновесия
отсутствуют перемещения в множителях
при силовых факторах.
Это имеет место в так называемых
расчётах по недеформированной схеме системы,
когда в уравнениях статики не учитываются
малые в сравнении с габаритами системы
изменения её геометрии ( координат точек )
в результате деформации элементов.
Слайд 4Общие свойства статически определимых систем (СОС)
1. Все силовые факторы в статически определимой
Общие свойства статически определимых систем (СОС)
1. Все силовые факторы в статически определимой
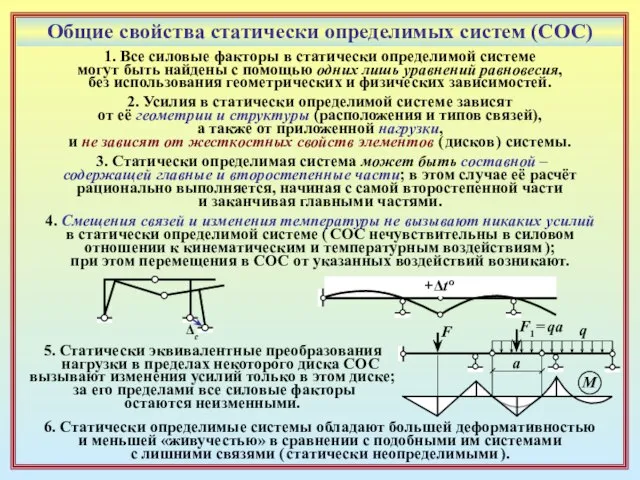
могут быть найдены с помощью одних лишь уравнений равновесия,
без использования геометрических и физических зависимостей.
5. Статически эквивалентные преобразования
нагрузки в пределах некоторого диска СОС
вызывают изменения усилий только в этом диске;
за его пределами все силовые факторы
остаются неизменными.
2. Усилия в статически определимой системе зависят
от её геометрии и структуры (расположения и типов связей),
а также от приложенной нагрузки,
и не зависят от жесткостных свойств элементов ( дисков ) системы.
3. Статически определимая система может быть составной –
содержащей главные и второстепенные части; в этом случае её расчёт
рационально выполняется, начиная с самой второстепенной части
и заканчивая главными частями.
4. Смещения связей и изменения температуры не вызывают никаких усилий
в статически определимой системе ( СОС нечувствительны в силовом
отношении к кинематическим и температурным воздействиям );
при этом перемещения в СОС от указанных воздействий возникают.
Δc
+Δt o
6. Статически определимые системы обладают большей деформативностью
и меньшей «живучестью» в сравнении с подобными им системами
с лишними связями ( статически неопределимыми ).
F
q
a
F1 = qa
M
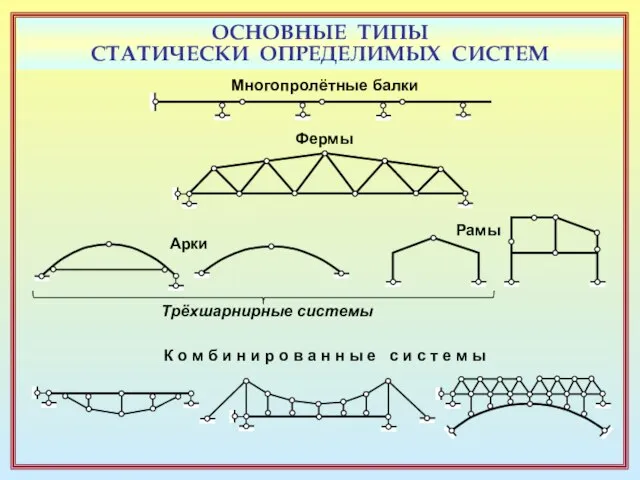
Слайд 5ОСНОВНЫЕ ТИПЫ
СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ СИСТЕМ
Многопролётные балки
Фермы
Арки
Рамы
Трёхшарнирные системы
К о м б и н
ОСНОВНЫЕ ТИПЫ
СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ СИСТЕМ
Многопролётные балки
Фермы
Арки
Рамы
Трёхшарнирные системы
К о м б и н
Слайд 6МНОГОПРОЛЁТНЫЕ
СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ
БАЛКИ
МНОГОПРОЛЁТНЫЕ
СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ
БАЛКИ

Слайд 7Многопролётная балка – это геометрически неизменяемая система,
состоящая из прямолинейных стержней –
Многопролётная балка – это геометрически неизменяемая система,
состоящая из прямолинейных стержней –

и расположенных так, что их продольные оси образуют единую прямую, с внешними связями (опорами) более чем в двух точках;
предназначена для работы на изгиб.
Кинематический анализ
а) количественный анализ:
W = 3D – 2H – C0
б) структурный анализ –
правила расположения связей:
– в пролёте не может быть более двух шарниров (в том числе более одного поступательного);
– суммарное число шарниров в двух смежных пролётах – не более трёх
(шарниры – цилиндрические или поперечные поступательные).
Для статически определимой многопролётной балки (МСОБ):
W = 0 С0 = 3D – 2H – необходимое число опорных связей.
M
Q
Q + dQ
M + dM
Слайд 8Основные структурные схемы многопролётных СО балок
…ш-ш – о-о – ш-ш – о-о…
…ш
Основные структурные схемы многопролётных СО балок
…ш-ш – о-о – ш-ш – о-о…
…ш
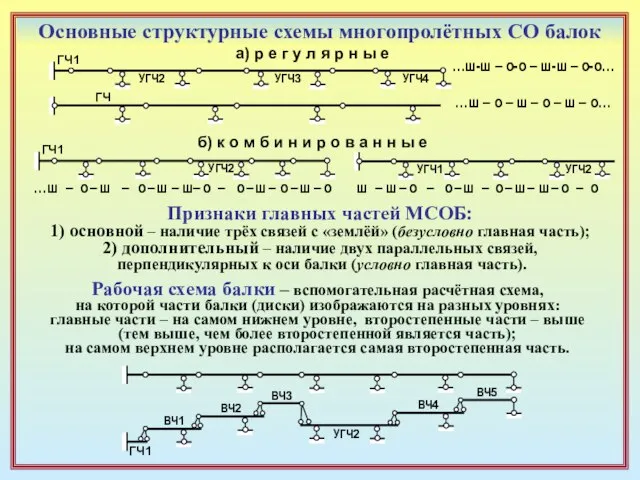
а) р е г у л я р н ы е
б) к о м б и н и р о в а н н ы е
…ш – о – ш – о – ш – ш– о – о – ш – о – ш – о
ш – ш – о – о – ш – о – ш – ш – о – о
Признаки главных частей МСОБ:
1) основной – наличие трёх связей с «землёй» (безусловно главная часть);
2) дополнительный – наличие двух параллельных связей,
перпендикулярных к оси балки (условно главная часть).
ГЧ1
ГЧ1
УГЧ1
УГЧ2
УГЧ2
УГЧ3
УГЧ4
ГЧ
УГЧ2
Рабочая схема балки – вспомогательная расчётная схема,
на которой части балки (диски) изображаются на разных уровнях:
главные части – на самом нижнем уровне, второстепенные части – выше
(тем выше, чем более второстепенной является часть);
на самом верхнем уровне располагается самая второстепенная часть.
ГЧ1
УГЧ2
ВЧ1
ВЧ2
ВЧ3
ВЧ4
ВЧ5
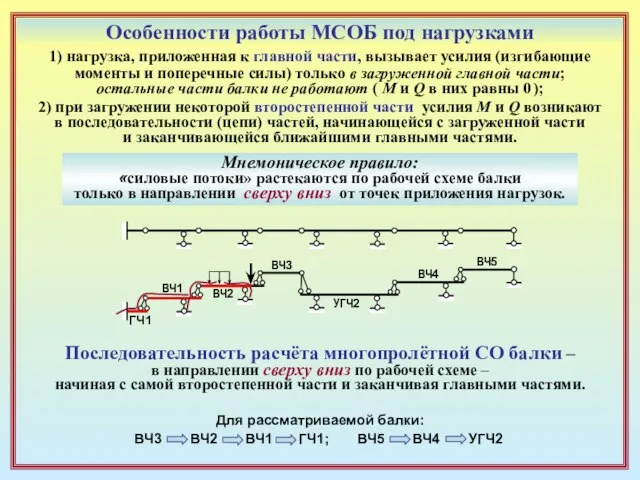
Слайд 9Особенности работы МСОБ под нагрузками
1) нагрузка, приложенная к главной части, вызывает усилия
Особенности работы МСОБ под нагрузками
1) нагрузка, приложенная к главной части, вызывает усилия

моменты и поперечные силы) только в загруженной главной части;
остальные части балки не работают ( M и Q в них равны 0 );
2) при загружении некоторой второстепенной части усилия M и Q возникают
в последовательности (цепи) частей, начинающейся с загруженной части
и заканчивающейся ближайшими главными частями.
ГЧ1
УГЧ2
ВЧ1
ВЧ2
ВЧ3
ВЧ4
ВЧ5
Мнемоническое правило:
«силовые потоки» растекаются по рабочей схеме балки
только в направлении сверху вниз от точек приложения нагрузок.
Слайд 101) нагрузка, приложенная к главной части, вызывает усилия (изгибающие
моменты и поперечные силы)
1) нагрузка, приложенная к главной части, вызывает усилия (изгибающие
моменты и поперечные силы)
остальные части балки не работают ( M и Q в них равны 0 );
2) при загружении некоторой второстепенной части усилия M и Q возникают
в последовательности (цепи) частей, начинающейся с загруженной части
и заканчивающейся ближайшими главными частями.
Последовательность расчёта многопролётной СО балки –
в направлении сверху вниз по рабочей схеме –
начиная с самой второстепенной части и заканчивая главными частями.
ГЧ1
УГЧ2
ВЧ1
ВЧ2
ВЧ3
ВЧ4
ВЧ5
Мнемоническое правило:
«силовые потоки» растекаются по рабочей схеме балки
только в направлении сверху вниз от точек приложения нагрузок.
Для рассматриваемой балки:
ВЧ3
ВЧ2
ВЧ1
ГЧ1;
ВЧ5
ВЧ4
УГЧ2
Особенности работы МСОБ под нагрузками
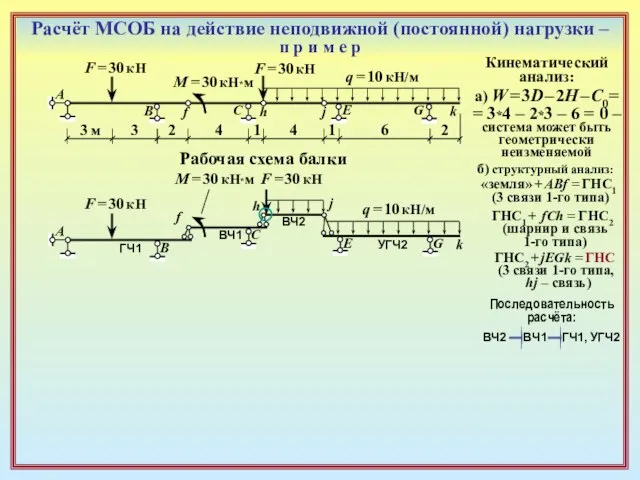
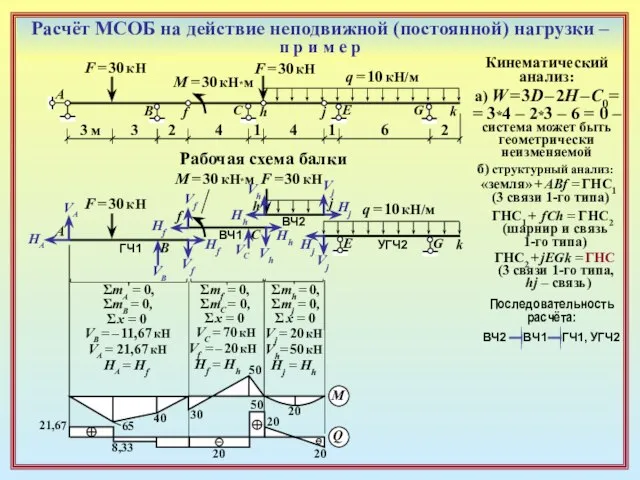
Слайд 11Расчёт МСОБ на действие неподвижной (постоянной) нагрузки – п р и м
Расчёт МСОБ на действие неподвижной (постоянной) нагрузки – п р и м
ГЧ1
УГЧ2
ВЧ2
ВЧ1
Кинематический
анализ:
а) W = 3D – 2H – C0=
= 3*4 – 2*3 – 6 = 0 – система может быть
геометрически
неизменяемой
A
B
C
E
G
f
h
k
j
б) структурный анализ:
«земля» + ABf = ГНС1
(3 связи 1-го типа)
ГНС1 + fCh = ГНС2
(шарнир и связь
1-го типа)
ГНС2 + jEGk = ГНС
(3 связи 1-го типа,
hj – связь)
Рабочая схема балки
A
B
C
E
G
f
h
k
j
F = 30 кН
F = 30 кН
F = 30 кН
F = 30 кН
М = 30 кН*м
М = 30 кН*м
q = 10 кН/м
q = 10 кН/м
3 м
6
3
2
4
4
2
1
1
Последовательность
расчёта:
ВЧ2
ВЧ1
ГЧ1,
УГЧ2
Слайд 12Расчёт МСОБ на действие неподвижной (постоянной) нагрузки – п р и м
Расчёт МСОБ на действие неподвижной (постоянной) нагрузки – п р и м
ГЧ1
УГЧ2
ВЧ2
ВЧ1
Кинематический
анализ:
а) W = 3D – 2H – C0=
= 3*4 – 2*3 – 6 = 0 – система может быть
геометрически
неизменяемой
A
B
C
E
G
f
h
k
j
б) структурный анализ:
«земля» + ABf = ГНС1
(3 связи 1-го типа)
ГНС1 + fCh = ГНС2
(шарнир и связь
1-го типа)
ГНС2 + jEGk = ГНС
(3 связи 1-го типа,
hj – связь)
Рабочая схема балки
A
B
C
E
G
f
h
k
j
F = 30 кН
F = 30 кН
F = 30 кН
F = 30 кН
М = 30 кН*м
q = 10 кН/м
q = 10 кН/м
3 м
6
3
2
4
4
2
1
1
Последовательность
расчёта:
ВЧ2
ВЧ1
ГЧ1,
УГЧ2
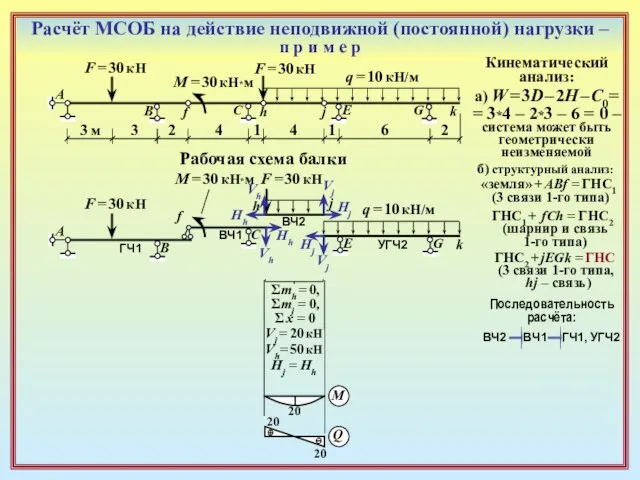
Vh
Vh
Vj
Vj
Hh
Hh
Hj
Hj
Σmh = 0,
Σmj = 0,
Σ x = 0
Vj = 20 кН
Vh= 50 кН
Hj = Hh
20
20
20
M
Q
М = 30 кН*м
Слайд 13Расчёт МСОБ на действие неподвижной (постоянной) нагрузки – п р и м
Расчёт МСОБ на действие неподвижной (постоянной) нагрузки – п р и м
ГЧ1
УГЧ2
ВЧ2
ВЧ1
Кинематический
анализ:
а) W = 3D – 2H – C0=
= 3*4 – 2*3 – 6 = 0 – система может быть
геометрически
неизменяемой
A
B
C
E
G
f
h
k
j
б) структурный анализ:
«земля» + ABf = ГНС1
(3 связи 1-го типа)
ГНС1 + fCh = ГНС2
(шарнир и связь
1-го типа)
ГНС2 + jEGk = ГНС
(3 связи 1-го типа,
hj – связь)
Рабочая схема балки
A
B
C
E
G
f
h
k
j
F = 30 кН
F = 30 кН
F = 30 кН
F = 30 кН
М = 30 кН*м
q = 10 кН/м
q = 10 кН/м
3 м
6
3
2
4
4
2
1
1
Последовательность
расчёта:
ВЧ2
ВЧ1
ГЧ1,
УГЧ2
Vh
Vh
Vj
Vj
Hh
Hh
Hj
Hj
Σmh = 0,
Σmj = 0,
Σ x = 0
Vj = 20 кН
Vh= 50 кН
Hj = Hh
20
20
20
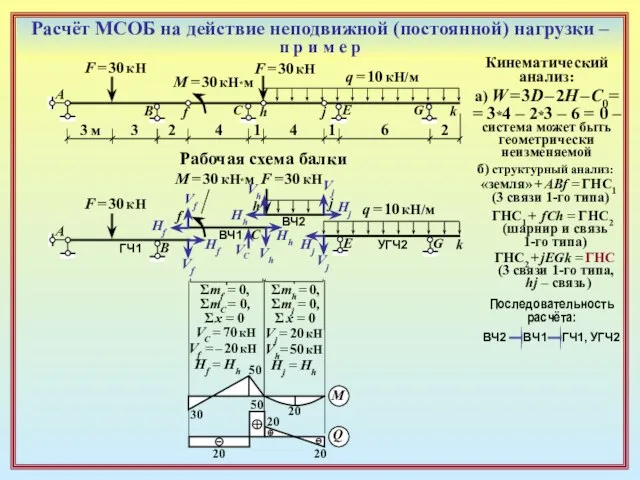
Σmf = 0,
ΣmC = 0,
Σ x = 0
VC = 70 кН
Vf = – 20 кН
Hf = Hh
M
Q
Vf
Hf
Hf
Vf
VC
50
30
50
20
М = 30 кН*м
Слайд 14Расчёт МСОБ на действие неподвижной (постоянной) нагрузки – п р и м
Расчёт МСОБ на действие неподвижной (постоянной) нагрузки – п р и м
ГЧ1
УГЧ2
ВЧ2
ВЧ1
Кинематический
анализ:
а) W = 3D – 2H – C0=
= 3*4 – 2*3 – 6 = 0 – система может быть
геометрически
неизменяемой
A
B
C
E
G
f
h
k
j
б) структурный анализ:
«земля» + ABf = ГНС1
(3 связи 1-го типа)
ГНС1 + fCh = ГНС2
(шарнир и связь
1-го типа)
ГНС2 + jEGk = ГНС
(3 связи 1-го типа,
hj – связь)
Рабочая схема балки
A
B
C
E
G
f
h
k
j
F = 30 кН
F = 30 кН
F = 30 кН
F = 30 кН
М = 30 кН*м
q = 10 кН/м
q = 10 кН/м
3 м
6
3
2
4
4
2
1
1
Последовательность
расчёта:
ВЧ2
ВЧ1
ГЧ1,
УГЧ2
Vh
Vh
Vj
Vj
Hh
Hh
Hj
Hj
Σmh = 0,
Σmj = 0,
Σ x = 0
Vj = 20 кН
Vh= 50 кН
Hj = Hh
20
20
20
Σmf = 0,
ΣmC = 0,
Σ x = 0
VC = 70 кН
Vf = – 20 кН
Hf = Hh
M
Q
Vf
Hf
Hf
Vf
VC
50
30
50
20
VA
HA
VB
ΣmA = 0,
ΣmB = 0,
Σ x = 0
VB = – 11,67 кН
VA = 21,67 кН
HA = Hf
65
40
21,67
8,33
М = 30 кН*м
Слайд 15Расчёт МСОБ на действие неподвижной (постоянной) нагрузки – п р и м
Расчёт МСОБ на действие неподвижной (постоянной) нагрузки – п р и м
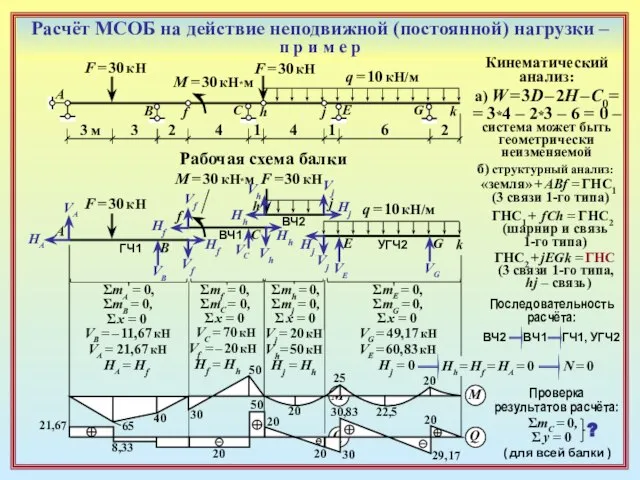
ГЧ1
УГЧ2
ВЧ2
ВЧ1
Кинематический
анализ:
а) W = 3D – 2H – C0=
= 3*4 – 2*3 – 6 = 0 – система может быть
геометрически
неизменяемой
A
B
C
E
G
f
h
k
j
б) структурный анализ:
«земля» + ABf = ГНС1
(3 связи 1-го типа)
ГНС1 + fCh = ГНС2
(шарнир и связь
1-го типа)
ГНС2 + jEGk = ГНС
(3 связи 1-го типа,
hj – связь)
Рабочая схема балки
A
B
C
E
G
f
h
k
j
F = 30 кН
F = 30 кН
F = 30 кН
F = 30 кН
М = 30 кН*м
q = 10 кН/м
q = 10 кН/м
3 м
6
3
2
4
4
2
1
1
Последовательность
расчёта:
ВЧ2
ВЧ1
ГЧ1,
УГЧ2
Vh
Vh
Vj
Vj
Hh
Hh
Hj
Hj
Σmh = 0,
Σmj = 0,
Σ x = 0
Vj = 20 кН
Vh= 50 кН
Hj = Hh
20
20
20
Σmf = 0,
ΣmC = 0,
Σ x = 0
VC = 70 кН
Vf = – 20 кН
Hf = Hh
M
Q
Vf
Hf
Hf
Vf
VC
50
30
50
20
VA
HA
VB
ΣmA = 0,
ΣmB = 0,
Σ x = 0
VB = – 11,67 кН
VA = 21,67 кН
HA = Hf
65
40
21,67
8,33
VE
VG
ΣmE = 0,
ΣmG = 0,
Σ x = 0
VG = 49,17 кН
VE = 60,83 кН
Hj = 0
Hh = Hf = HA = 0
N = 0
M
Q
20
25
22,5
30
20
30,83
29,17
Проверка
результатов расчёта:
ΣmС = 0,
Σ y = 0
?
( для всей балки )
М = 30 кН*м
Слайд 16Расчёт МСОБ на временные (подвижные) нагрузки
с помощью линий влияния
Построение линий влияния
Расчёт МСОБ на временные (подвижные) нагрузки
с помощью линий влияния
Построение линий влияния

статическим методом
Варианты:
1) полное решение – выявление линейных выражений S(x) по характерным участкам
расположения единичного груза F = 1; границы участков – границы дисков (элементов
балки) + сечение с определяемым усилием S(x);
2) использование типовых линий влияния для однопролётной балки.
A
B
1
1
l
a
b
c
d
F = 1
x
VA
VB
Линии влияния опорных реакций
Груз F =1 – в произвольной точке балки
ΣmА = 0,
ΣmВ = 0
VB = x / l;
VA = 1 – x / l;
при х = 0: VA = 1; VB = 0;
при х = l : VA = 0; VB = 1.
Линии влияния M1 и Q1 в межопорном сечении 1-1
а) груз F =1 слева от сечения
уравнения
левых
прямых
при х = 0: M1 = 0; Q1 = 0;
при х = a – 0: M1 = ab/l; Q1 = – a/l
Л.В. VA
Л.В. VB
б) груз F =1 справа от сечения
уравнения
правых
прямых
при х = l: M1 = 0; Q1 = 0.
при х = a + 0: M1 = ab/l; Q1 = b/l ;
0
0
1
1
0
0
a
b
Л.В. M1
Левая
прямая
Правая прямая
Правая прямая
0
0
Левая
прямая
Л.В. Q1
a/l
b/l
Параллельные
1
Слайд 17Расчёт МСОБ на временные (подвижные) нагрузки
с помощью линий влияния
Построение линий влияния
Расчёт МСОБ на временные (подвижные) нагрузки
с помощью линий влияния
Построение линий влияния
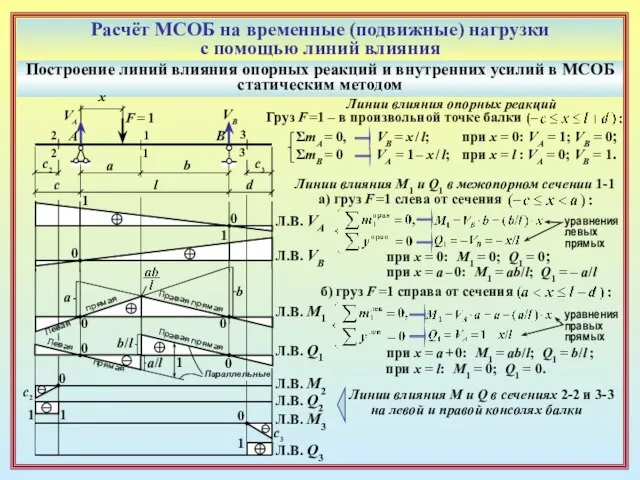
статическим методом
A
B
1
1
2
2
3
3
l
a
b
c
d
F = 1
x
VA
VB
Линии влияния опорных реакций
Груз F =1 – в произвольной точке балки
ΣmА = 0,
ΣmВ = 0
VB = x / l;
VA = 1 – x / l;
при х = 0: VA = 1; VB = 0;
при х = l : VA = 0; VB = 1.
Линии влияния M1 и Q1 в межопорном сечении 1-1
а) груз F =1 слева от сечения
уравнения
левых
прямых
при х = 0: M1 = 0; Q1 = 0;
при х = a – 0: M1 = ab/l; Q1 = – a/l
Л.В. VA
Л.В. VB
б) груз F =1 справа от сечения
уравнения
правых
прямых
при х = l: M1 = 0; Q1 = 0.
при х = a + 0: M1 = ab/l; Q1 = b/l ;
0
0
1
1
0
0
a
b
Л.В. M1
Левая
прямая
Правая прямая
Правая прямая
0
0
Левая
прямая
Л.В. Q1
a/l
b/l
Параллельные
1
Линии влияния M и Q в сечениях 2-2 и 3-3
на левой и правой консолях балки
c2
c3
Л.В. Q2
Л.В. Q3
Л.В. M2
Л.В. M3
c2
1
0
1
0
c3
1
Слайд 18Расчёт МСОБ на временные (подвижные) нагрузки
с помощью линий влияния
Построение линий влияния
Расчёт МСОБ на временные (подвижные) нагрузки
с помощью линий влияния
Построение линий влияния
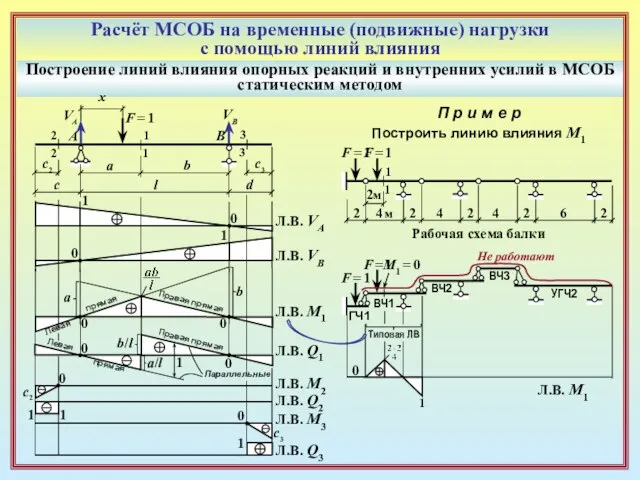
статическим методом
A
B
1
1
2
2
3
3
l
a
b
c
d
F = 1
x
VA
VB
Л.В. VA
Л.В. VB
0
0
1
1
0
0
a
b
Л.В. M1
Левая
прямая
Правая прямая
Правая прямая
0
0
Левая
прямая
Л.В. Q1
a/l
b/l
Параллельные
1
c2
c3
Л.В. Q2
Л.В. Q3
Л.В. M2
Л.В. M3
c2
1
0
1
0
c3
1
ГЧ1
УГЧ2
ВЧ1
ВЧ2
ВЧ3
2
2
2
2
2
4 м
6
4
4
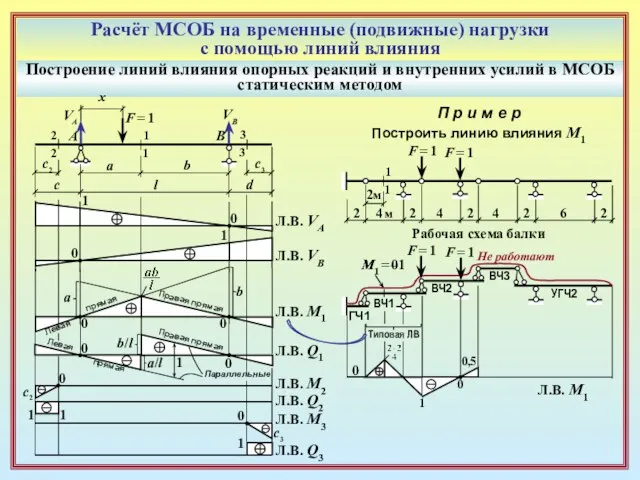
П р и м е р
Построить линию влияния М1
1
1
2м
Рабочая схема балки
F = 1
F = 1
Не работают
М1 = 0
0
F = 1
F = 1
Л.В. M1
Типовая ЛВ
1
Слайд 19Расчёт МСОБ на временные (подвижные) нагрузки
с помощью линий влияния
Построение линий влияния
Расчёт МСОБ на временные (подвижные) нагрузки
с помощью линий влияния
Построение линий влияния
статическим методом
A
B
1
1
2
2
3
3
l
a
b
c
d
F = 1
x
VA
VB
Л.В. VA
Л.В. VB
0
0
1
1
0
0
a
b
Л.В. M1
Левая
прямая
Правая прямая
Правая прямая
0
0
Левая
прямая
Л.В. Q1
a/l
b/l
Параллельные
1
c2
c3
Л.В. Q2
Л.В. Q3
Л.В. M2
Л.В. M3
c2
1
0
1
0
c3
1
ГЧ1
УГЧ2
ВЧ1
ВЧ2
ВЧ3
2
2
2
2
2
4 м
6
4
4
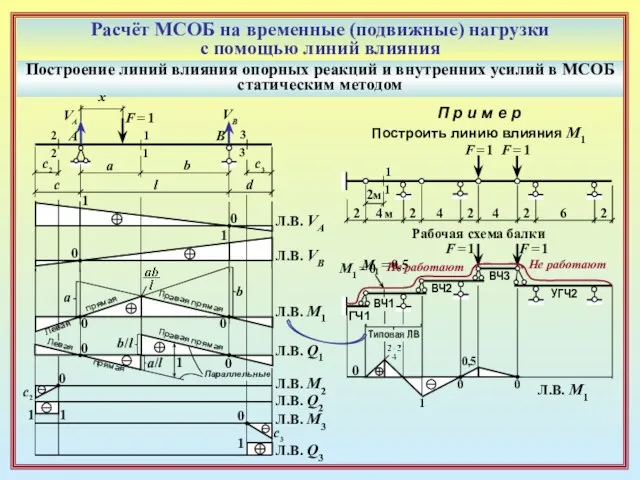
П р и м е р
Построить линию влияния М1
1
1
2м
Рабочая схема балки
F = 1
Не работают
М1 = 0
0
F = 1
F = 1
Типовая ЛВ
1
F = 1
М1 = –1
0
0,5
Л.В. M1
Слайд 20Расчёт МСОБ на временные (подвижные) нагрузки
с помощью линий влияния
Построение линий влияния
Расчёт МСОБ на временные (подвижные) нагрузки
с помощью линий влияния
Построение линий влияния
статическим методом
A
B
1
1
2
2
3
3
l
a
b
c
d
F = 1
x
VA
VB
Л.В. VA
Л.В. VB
0
0
1
1
0
0
a
b
Л.В. M1
Левая
прямая
Правая прямая
Правая прямая
0
0
Левая
прямая
Л.В. Q1
a/l
b/l
Параллельные
1
c2
c3
Л.В. Q2
Л.В. Q3
Л.В. M2
Л.В. M3
c2
1
0
1
0
c3
1
ГЧ1
УГЧ2
ВЧ1
ВЧ2
ВЧ3
2
2
2
2
2
4 м
6
4
4
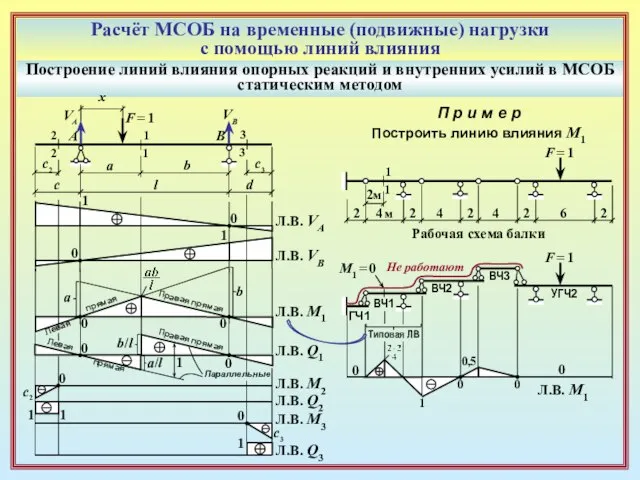
П р и м е р
Построить линию влияния М1
1
1
2м
Рабочая схема балки
F = 1
Не работают
М1 = 0,5
0
F = 1
F = 1
Типовая ЛВ
1
F = 1
0
0,5
Не работают
М1 = 0
0
Л.В. M1
Слайд 21Расчёт МСОБ на временные (подвижные) нагрузки
с помощью линий влияния
Построение линий влияния
Расчёт МСОБ на временные (подвижные) нагрузки
с помощью линий влияния
Построение линий влияния
статическим методом
A
B
1
1
2
2
3
3
l
a
b
c
d
F = 1
x
VA
VB
Л.В. VA
Л.В. VB
0
0
1
1
0
0
a
b
Л.В. M1
Левая
прямая
Правая прямая
Правая прямая
0
0
Левая
прямая
Л.В. Q1
a/l
b/l
Параллельные
1
c2
c3
Л.В. Q2
Л.В. Q3
Л.В. M2
Л.В. M3
c2
1
0
1
0
c3
1
ГЧ1
УГЧ2
ВЧ1
ВЧ2
ВЧ3
2
2
2
2
2
4 м
6
4
4
П р и м е р
Построить линию влияния М1
1
1
2м
Рабочая схема балки
F = 1
0
Типовая ЛВ
1
F = 1
0
0,5
Не работают
М1 = 0
0
0
Л.В. M1
Слайд 22Расчёт МСОБ на временные (подвижные) нагрузки
с помощью линий влияния
Построение линий влияния
Расчёт МСОБ на временные (подвижные) нагрузки
с помощью линий влияния
Построение линий влияния

алгоритм и пример рассмотрены в теме
«Построение линий влияния силовых факторов кинематическим методом»
1
2
3
c
D
F = 20 кН
Требуется построить объемлющую эпюру М
на участке cD
Л.В. M2
Расчётные усилия в МСОБ и их эпюры ( объемлющие эпюры )
Mрасч=
Mmax = Mconst+ Σ Mtemp,max
Qрасч=
Mсоотв
F = 20 кН
q = 12 кН/м
F2
F1
p = 10 кН/м
p = 10 кН/м
q , F – постоянные нагрузки
p , F1 , F2 – временные нагрузки
F1 = 16 кН,
F2 = 18 кН
3
7
5
6
4
2 м
4
6
2
2
2
2
2
Mmin = Mconst+ Σ Mtemp,min
Qmax= Qconst+ Σ Qtemp,max
Qmin = Qconst+ Σ Qtemp,min
Расчётные сечения 1, 2, … ,7
1
1
1,5
1,5
1,5
1,5
20
20
52
18
12,5
3,5
Эпюра Mconst
( кН*м )
1
2
1
0,5
Л.В. M3
Л.В. M4
1,125
1,5
0,75
0,5
Слайд 23Расчёт МСОБ на временные (подвижные) нагрузки
с помощью линий влияния
Построение линий влияния
Расчёт МСОБ на временные (подвижные) нагрузки
с помощью линий влияния
Построение линий влияния

алгоритм и пример рассмотрены в теме
«Построение линий влияния силовых факторов кинематическим методом»
1
2
3
c
D
F = 20 кН
Требуется построить объемлющую эпюру М
на участке cD
Расчётные усилия в МСОБ и их эпюры ( объемлющие эпюры )
Mрасч=
Mmax = Mconst+ Σ Mtemp,max
Qрасч=
Mсоотв
F = 20 кН
q = 12 кН/м
F2
F1
p = 10 кН/м
p = 10 кН/м
q , F – постоянные нагрузки
p , F1 , F2 – временные нагрузки
F1 = 16 кН,
F2 = 18 кН
3
7
5
6
4
2 м
4
6
2
2
2
2
2
Mmin = Mconst+ Σ Mtemp,min
Qmax= Qconst+ Σ Qtemp,max
Qmin = Qconst+ Σ Qtemp,min
Расчётные сечения 1, 2, … ,7
1
1
1,5
1,5
1,5
1,5
20
20
52
18
12,5
3,5
Эпюра Mconst
( кН*м )
Л.В. M4
1,125
1,5
0,75
0,5
F2
F1
p
p
F2
F1
p
p
Загружение
на max M4, temp
Загружение
на min M4, temp
M4, temp,max= 66 кН*м
M4, temp,min= – 93 кН*м
M4, max= M4, const + M4, temp, max=
= – 3,5 + 66 = 62,5 кН*м
M4, min= M4, const + M4, temp, min=
= – 3,5 – 93 = – 96,5 кН*м
Аналогично
для остальных сечений
Слайд 24Расчёт МСОБ на временные (подвижные) нагрузки
с помощью линий влияния
Построение линий влияния
Расчёт МСОБ на временные (подвижные) нагрузки
с помощью линий влияния
Построение линий влияния

алгоритм и пример рассмотрены в теме
«Построение линий влияния силовых факторов кинематическим методом»
1
2
3
c
D
F = 20 кН
Требуется построить объемлющую эпюру М
на участке cD
Расчётные усилия в МСОБ и их эпюры ( объемлющие эпюры )
Mрасч=
Mmax = Mconst+ Σ Mtemp,max
Qрасч=
Mсоотв
F = 20 кН
q = 12 кН/м
F2
F1
p = 10 кН/м
p = 10 кН/м
q , F – постоянные нагрузки
p , F1 , F2 – временные нагрузки
F1 = 16 кН,
F2 = 18 кН
3
7
5
6
4
2 м
4
6
2
2
2
2
2
Mmin = Mconst+ Σ Mtemp,min
Qmax= Qconst+ Σ Qtemp,max
Qmin = Qconst+ Σ Qtemp,min
1
1
1,5
1,5
1,5
1,5
20
20
52
18
12,5
3,5
Эпюра Mconst
( кН*м )
Объемлющая
эпюра M
( кН*м )
146
122
95
Mmin
Mmax
Слайд 25К о н т р о л ь н ы е в
К о н т р о л ь н ы е в

( в скобках даны номера слайдов, на которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 25» )
1. Какие системы называются статически определимыми? ( 2 )
2. При выполнении каких условий система может рассматриваться как статически определимая? ( 2 )
3. Может ли быть статически неопределимой задача определения усилий в системе
без лишних связей? ( 2 )
4. Является ли статически определимой система без лишних связей, рассчитываемая
по деформированной схеме? ( 2, 3 )
5. Какими общими свойствами обладают все статически определимые системы? ( 4 )
6. Если в статически определимой системе изменить жёсткости некоторых элементов,
то приведет ли это к изменению силовых факторов при той же нагрузке? ( 4 )
7. Как статически определимая система реагирует на изменение температуры или смещения связей? Оценить статически и кинематически. ( 4 ) 7. Как статически определимая система реагирует на изменение температуры или смещения связей? Оценить статически и кинематически. ( 4 )
8. Каковы основные типы статически определимых систем? ( 5 )
9. Что такое многопролётная балка? ( 7 )
10. Особенности кинематического анализа многопролётных балок. ( 7 )
Правила расположения опор и шарниров в многопролётной статически определимой
балке ( МСОБ ). ( 7 )
11. Каковы основные структурные схемы МСОБ? ( 8 )
12. По каким признакам определяются главные части МСОБ? ( 8 )
13. Что такое рабочая схема многопролётной СО балки? ( 8 )
14. Как располагаются на рабочей схеме главные и второстепенные части балки? ( 8 )
15. Как работают части МСОБ при локальном загружении
а) главной части? ( 9 ) а) главной части? ( 9 ) б) второстепенной части? ( 9 )
_____________________________________________________________
*) Только в режиме «Показ слайдов»
 Процессы жизнедеятельности одноклеточных животных
Процессы жизнедеятельности одноклеточных животных Живой организм и его свойства
Живой организм и его свойства Финансирование научных исследований
Финансирование научных исследований Операционные системы и сети ЭВМ Operating Systems and Networking Лекция 26
Операционные системы и сети ЭВМ Operating Systems and Networking Лекция 26 АЙСБЕРГ
АЙСБЕРГ Морфология культуры
Морфология культуры Онлайн-курс СПбПУ. Введение в инженерную деятельность. Трек 2
Онлайн-курс СПбПУ. Введение в инженерную деятельность. Трек 2 Органическая химия. Предельные углеводороды
Органическая химия. Предельные углеводороды Безопасность жизни
Безопасность жизни Май 2012
Май 2012 Реализация производственной системы Сбербанка в Западно-Уральском банке ОАО Сбербанка России: задачи, инструменты, достижения
Реализация производственной системы Сбербанка в Западно-Уральском банке ОАО Сбербанка России: задачи, инструменты, достижения кодировка
кодировка Сырные палочки
Сырные палочки Первая встреча Костромского Клуба Тестировщиков (ClubQA)Что должен знать тестировщик
Первая встреча Костромского Клуба Тестировщиков (ClubQA)Что должен знать тестировщик Сущность и содержание миссии. Формулирование миссии
Сущность и содержание миссии. Формулирование миссии 3_urok_9-e_kl_informatika
3_urok_9-e_kl_informatika Dlya_postera
Dlya_postera Схема расположения участка в структуре города
Схема расположения участка в структуре города От газеты Телесемь в Краснодаре
От газеты Телесемь в Краснодаре Презентация на тему: Красная Шапочка
Презентация на тему: Красная Шапочка Решение нестандартных уравнений
Решение нестандартных уравнений СЧЕТ ОТ 0 ДО 10
СЧЕТ ОТ 0 ДО 10 Модель психологической службы ГБОУ СОШ № 426
Модель психологической службы ГБОУ СОШ № 426 Где живут люди? ИЗО 4 класс
Где живут люди? ИЗО 4 класс С ДНЕМ УЧИТЕЛЯ! В большую жизнь Вы нам открыли двери,Вы нас не только азбуке учили.Учитель! Мы Вас любим, мы Вам верим!Мы доброты ур
С ДНЕМ УЧИТЕЛЯ! В большую жизнь Вы нам открыли двери,Вы нас не только азбуке учили.Учитель! Мы Вас любим, мы Вам верим!Мы доброты ур Простые механизмы. Рычаг.
Простые механизмы. Рычаг. MTC Skills
MTC Skills Исторические лица земли Тверской, их жизнь и деяния, составляющие гордость региона
Исторические лица земли Тверской, их жизнь и деяния, составляющие гордость региона