Содержание
- 2. План 1. Означення степеневої функції. 2. Властивості та графік функції де 3. Властивості та графік функції
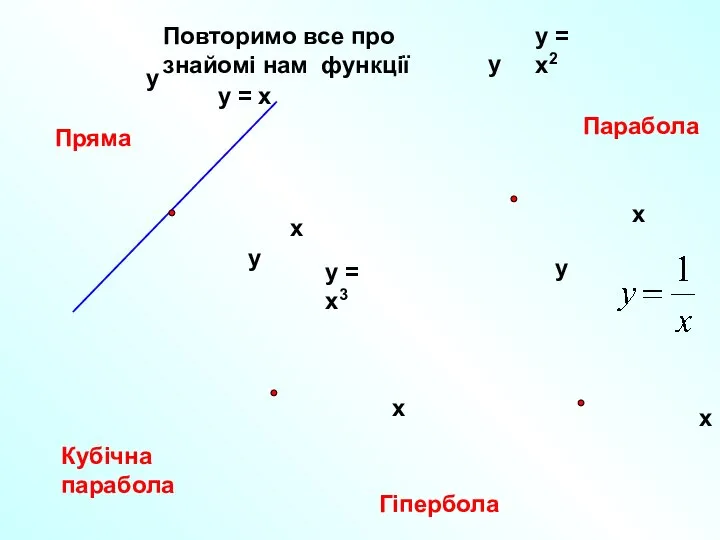
- 4. Повторимо все про знайомі нам функції Пряма Парабола Кубічна парабола Гіпербола
- 5. Всі ці функції є частковими випадками степеневої функції Властивості і графік степеневої функції залежать від властивостей
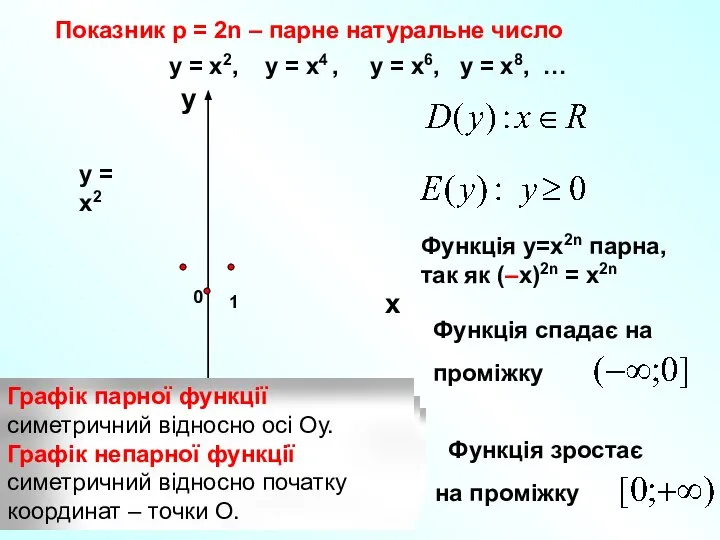
- 6. Показник р = 2n – парне натуральне число 1 0 х у у = х2, у
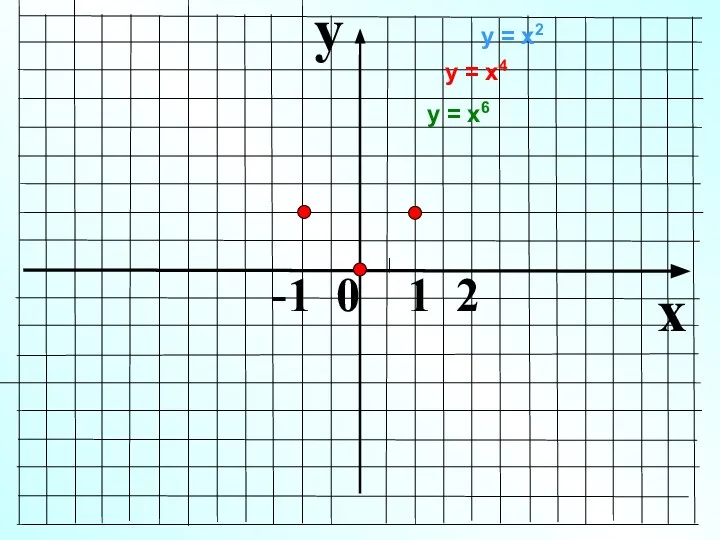
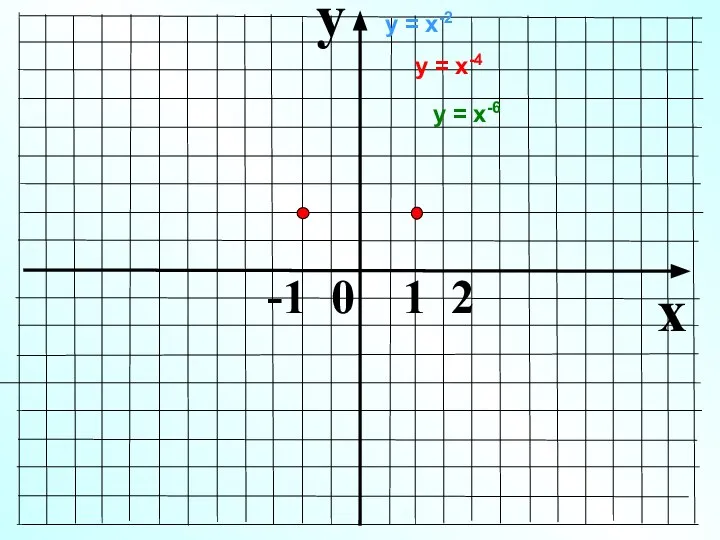
- 7. y x -1 0 1 2 у = х2 у = х6 у = х4
- 8. Показник р = 2n-1 – непарне натуральне число 1 х у у = х3, у =
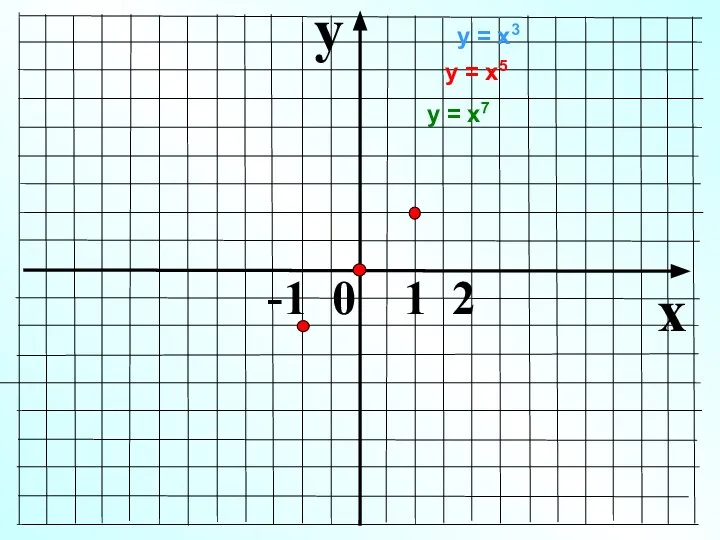
- 9. y x -1 0 1 2 у = х3 у = х7 у = х5
- 10. Показник р = – 2n, де n – натуральне число 1 0 х у у =
- 11. y x -1 0 1 2 у = х-4 у = х-2 у = х-6
- 12. Показник р = – (2n-1), де n – натуральне число 1 0 х у у =
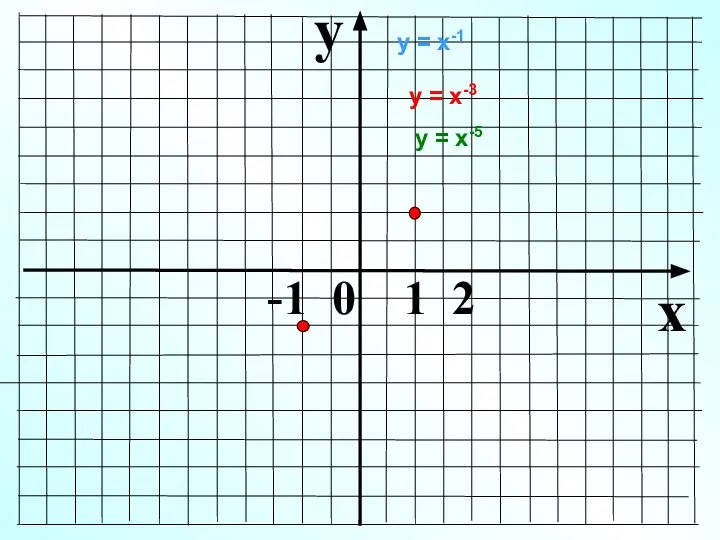
- 13. y x -1 0 1 2 у = х-1 у = х-3 у = х-5
- 14. 0 Показник р – додатне дійсне неціле число 1 х у у = х1,3, у =
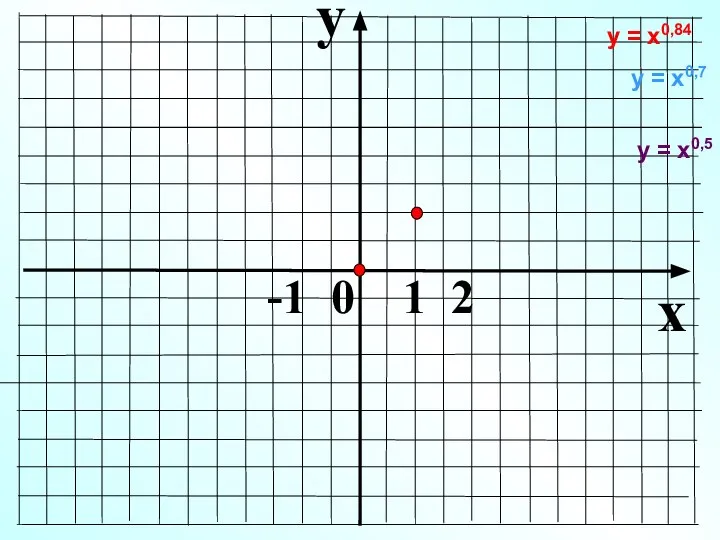
- 15. y x -1 0 1 2 у = х0,5 у = х0,84 у = х0,7
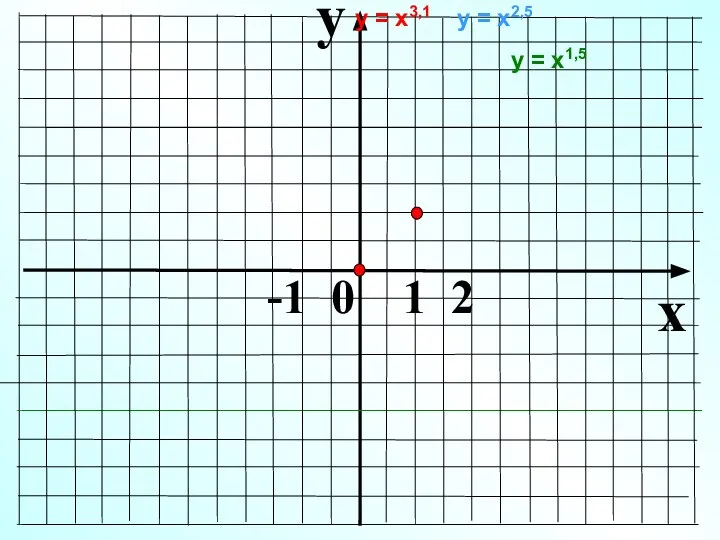
- 16. y x -1 0 1 2 у = х1,5 у = х2,5 у = х3,1
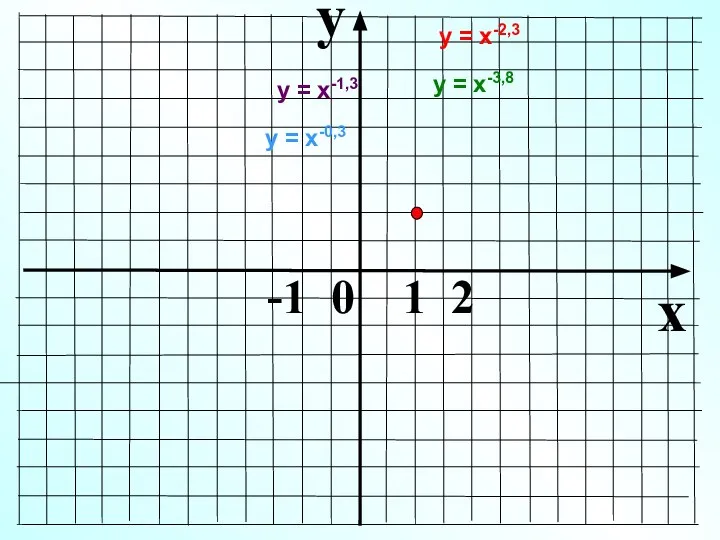
- 17. 0 Показник р – від’ємне дійсне неціле число 1 х у у = х-1,3, у =
- 18. y x -1 0 1 2 у = х-1,3 у = х-0,3 у = х-2,3 у
- 20. Розв'язок завдання
- 22. Скачать презентацию










 Бытовой и портретный жанры в русской живописи второй половины 19 века
Бытовой и портретный жанры в русской живописи второй половины 19 века Системы автоматизации и телеметрии газорегуляторных пунктов. Внедрение типовых технических решений в ГРС
Системы автоматизации и телеметрии газорегуляторных пунктов. Внедрение типовых технических решений в ГРС Мультипликация – это весело!
Мультипликация – это весело! Моральные проблемы суррогатного материнства
Моральные проблемы суррогатного материнства «О роли вузов культуры и искусств в создании электронно-библиотечных систем»
«О роли вузов культуры и искусств в создании электронно-библиотечных систем» В ожидании грядущего Царства
В ожидании грядущего Царства KiwiFest. Jack & Jill
KiwiFest. Jack & Jill Туринский многопрофильный техникум
Туринский многопрофильный техникум Психолингвистика в криминалистике и судебной психологии
Психолингвистика в криминалистике и судебной психологии Популяризация службы в вооруженных силах и профилактика асоциального поведения военнослужащих
Популяризация службы в вооруженных силах и профилактика асоциального поведения военнослужащих rossiya_nasha_rodina (1)
rossiya_nasha_rodina (1) Множественность денежных единиц
Множественность денежных единиц Сварочное оборудование
Сварочное оборудование СТАТИСТИКА ОСНОВНЫХ И ОБОРОТНЫХ ФОНДОВ
СТАТИСТИКА ОСНОВНЫХ И ОБОРОТНЫХ ФОНДОВ Функция y = cos x. Ее свойства и график
Функция y = cos x. Ее свойства и график Материнский капитал в РФ. Понятие материнского капитала
Материнский капитал в РФ. Понятие материнского капитала Мобильная коммерция на рынке розничных платежей
Мобильная коммерция на рынке розничных платежей Растения и животные водоёмов Казахстана
Растения и животные водоёмов Казахстана Товарная политика
Товарная политика Голодні ігри
Голодні ігри ТЕМА № 2 (ХПИ)
ТЕМА № 2 (ХПИ) Балансовый метод отражения информации
Балансовый метод отражения информации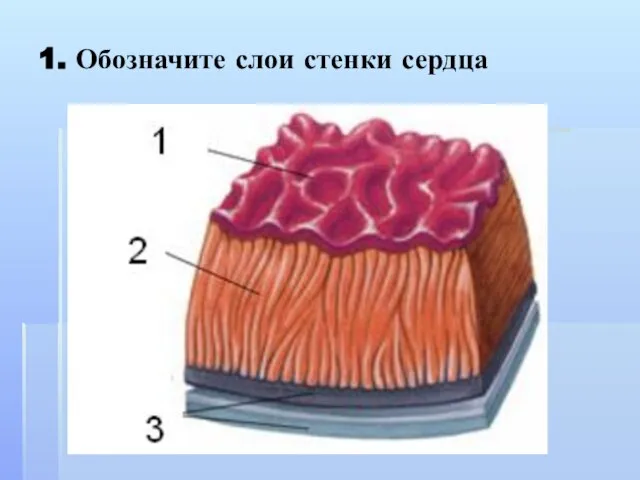 1. Обозначите слои стенки сердца
1. Обозначите слои стенки сердца Приготовление пресного сдобного теста и изделий из него
Приготовление пресного сдобного теста и изделий из него …Mass Media и реклама – 20 лет спустя
…Mass Media и реклама – 20 лет спустя «ЛИФБА БАЙРАМЫ
«ЛИФБА БАЙРАМЫ «Программируемые устройства вокруг нас»поисково-исследовательская работа
«Программируемые устройства вокруг нас»поисково-исследовательская работа ТО и ремонт гидроаппарптуры
ТО и ремонт гидроаппарптуры