Степенная функция

Рассмотрим степенные функции с натуральным показателем а, принадлежащим ко множеству всех натуральных чисел. Если а≠0, то в степень а можно возвести любое действительное число. Поэтому областью определения функции у =xа является множество всех действительных чисел. С некоторыми такими степенными функциями с натуральным показателем мы уже знакомы.

Если а=0, то степень х0 определена для любого числа х≠0.
При этом х0=1 функция у=х0 определена на множестве Х=(-∞; 0) и (0;∞) и её графиком является параллельная оси Ох прямая у=1 с одной «выколотой» точкой (0;1).

Если а=1, то получим функцию у = х, её графиком является прямая.

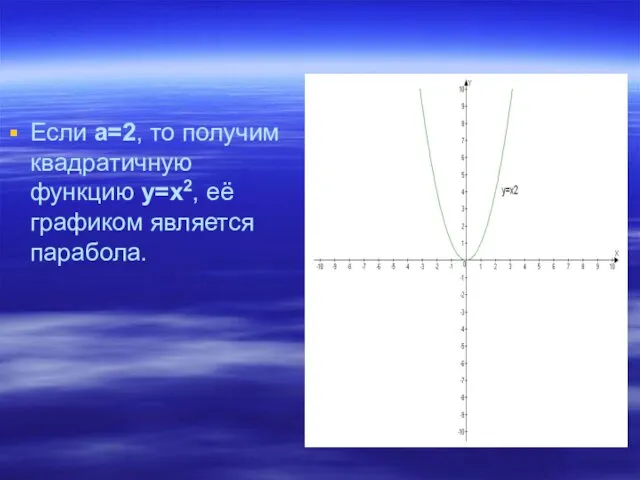
Если а=2, то получим квадратичную функцию у=х2, её графиком является парабола.

Функция у=х3, или кубическая функция. Чем большее число возводится в куб, тем больший результат получается. Поэтому кубическая функция является возрастающей. График у=х3 называется кубической параболой.

Функция у=х4 . График функции у=х4 называется параболой четвёртого порядка. Этот график симметричен относительно оси ординат.

Функция у = х2n ,где n принадлежит множеству целых положительных чисел. Степенная функция такого вида имеет чётный положительный показатель степени а=2n. Так как всегда х2n=(-х)2n, то графики всех таких функций симметричны относительно оси ординат. Все функции вида у = х2n, n принадлежит множеству целых положительных чисел имеют следующие одинаковые свойства:
Х=R Х ↑ =(-∞;∞)
У=[0;∞) Х ↓ =ǿ
Х0={0}
Х+= (0;∞)
Х-= (-∞;0)

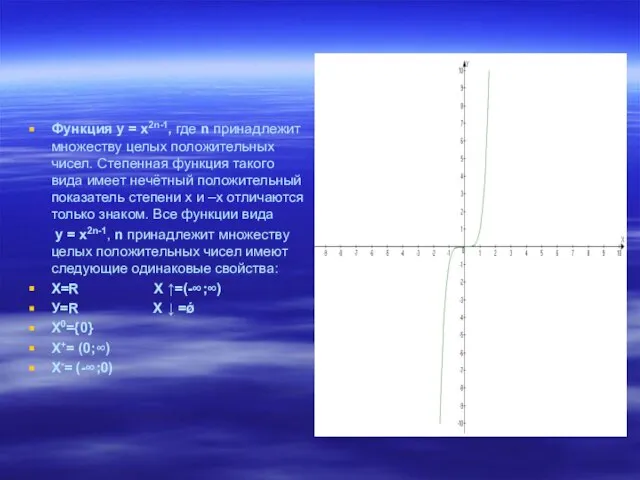
Функция у = х2n-1, где n принадлежит множеству целых положительных чисел. Степенная функция такого вида имеет нечётный положительный показатель степени х и –х отличаются только знаком. Все функции вида
у = х2n-1, n принадлежит множеству целых положительных чисел имеют следующие одинаковые свойства:
Х=R Х ↑=(-∞;∞)
У=R Х ↓ =ǿ
Х0={0}
Х+= (0;∞)
Х-= (-∞;0)

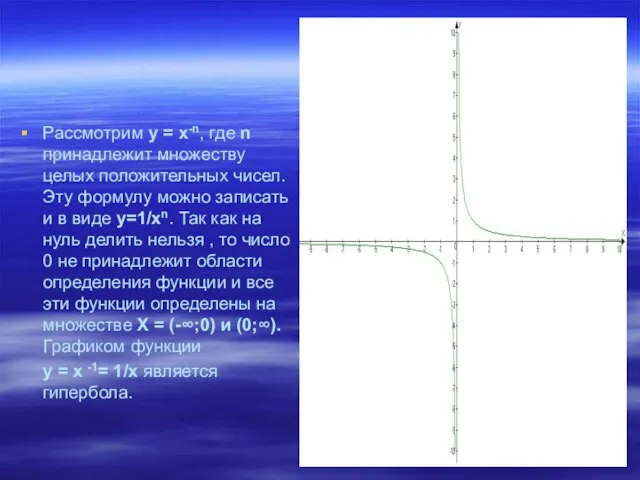
Рассмотрим у = х-n, где n принадлежит множеству целых положительных чисел. Эту формулу можно записать и в виде у=1/хn. Так как на нуль делить нельзя , то число 0 не принадлежит области определения функции и все эти функции определены на множестве Х = (-∞;0) и (0;∞). Графиком функции
у = х -1= 1/х является гипербола.

Функция у=х-2, или у=1/x2.
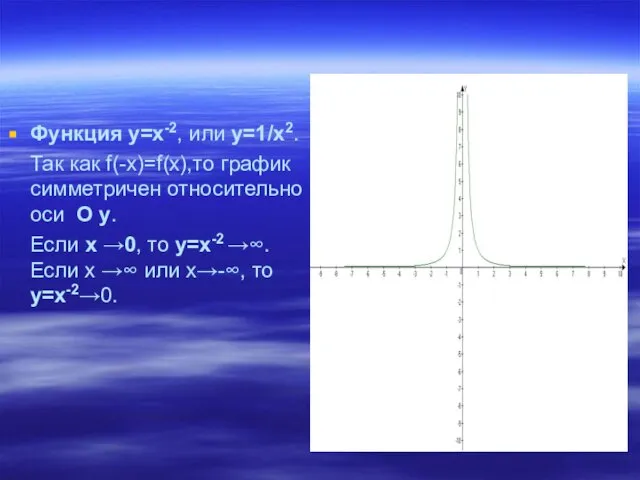
Так как f(-x)=f(x),то график симметричен относительно оси О у.
Если х →0, то у=х-2 →∞. Если х →∞ или х→-∞, то у=х-2→0.