Содержание
- 2. Вы знакомы с функциями у=х, у=х2, у=хЗ, y=1/х и т. д. Все эти функции являются частными
- 3. Виды степенной функции 1. Показатель р=2n - четное натуральное число. В этом случае степенная функция у
- 4. Рис. 1
- 5. 2. Показатель р=2n-1 - нечетное натуральное число. В этом случае степенная функция y=х2n-1, где 2n-1 -
- 6. 3. Показатель р = - 2n, где n - натуральное число. В этом случае степенная функция
- 7. 4. Показатель р = - (2n - 1), где n - натуральное число. В этом случае
- 8. 5. Показатель р - положительное действительное нецелое число. В этом случае функция у=хР обладает следующими свойствами:
- 10. Скачать презентацию
Слайд 2Вы знакомы с функциями у=х, у=х2, у=хЗ, y=1/х и т. д. Все
Вы знакомы с функциями у=х, у=х2, у=хЗ, y=1/х и т. д. Все

Слайд 3Виды степенной функции
1. Показатель р=2n - четное натуральное число. В этом случае
Виды степенной функции
1. Показатель р=2n - четное натуральное число. В этом случае

- область определения - все действительные числа, т. е. множество R ;
- множество значений - неотрицательные числа, т. е. y≥ 0;
функция у=х2n четная, так как (-х)2n = х2n;
- функция является убывающей на промежутке x≥O и возрастающей на промежутке x≤ O.
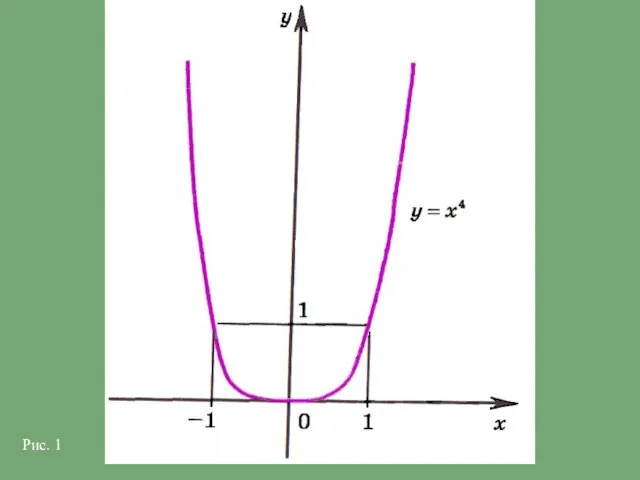
График функции у = хР имеет такой же вид, как, например, график функции у = х4 (рис. 1).
Слайд 4Рис. 1
Рис. 1
Слайд 52. Показатель р=2n-1 - нечетное натуральное число.
В этом случае степенная функция
2. Показатель р=2n-1 - нечетное натуральное число.
В этом случае степенная функция
- область определения - множество R;
- множество значений - множество R;
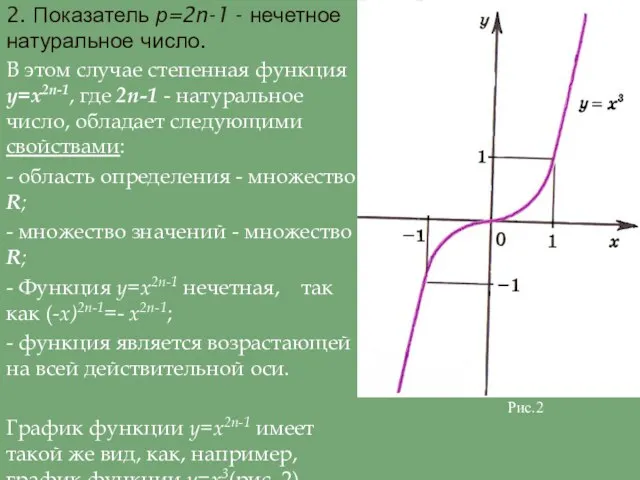
- Функция y=х2n-1 нечетная, так как (-х)2n-1=- х2n-1;
- функция является возрастающей на всей действительной оси.
График функции y=х2n-1 имеет такой же вид, как, например, график функции y=х3(рис. 2).
Рис.2
Слайд 63. Показатель р = - 2n, где n - натуральное число.
В
3. Показатель р = - 2n, где n - натуральное число.
В
- область определения - множество R, кроме х= 0;
- множество значений - положительные числа у>0;
- Функция y=х2n- четная, так как (-х)2n =х2n;
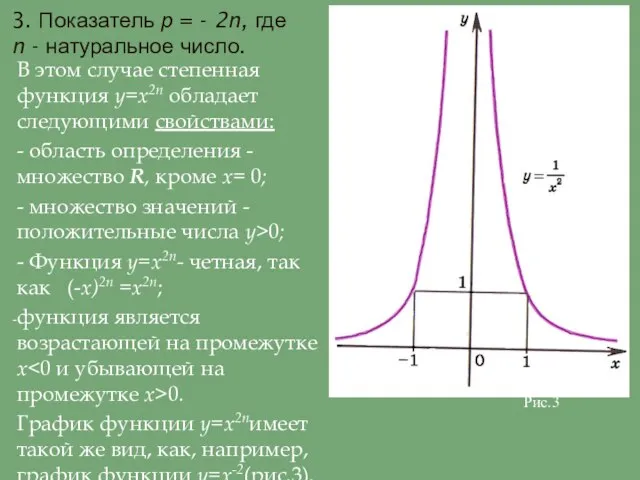
функция является возрастающей на промежутке х<0 и убывающей на промежутке х>0.
График функции y=х2nимеет такой же вид, как, например, график функции y=х-2(рис.3).
Рис.3
Слайд 74. Показатель р = - (2n - 1), где n - натуральное
4. Показатель р = - (2n - 1), где n - натуральное
В этом случае степенная функция y=х-(2n-1) обладает следующими свойствами:
- область определения - множество R, кроме х=0;
- множество значений - множество R, кроме у=0;
- функция нечетная, так как (-х)-(2n-1) = х-(2n-1);
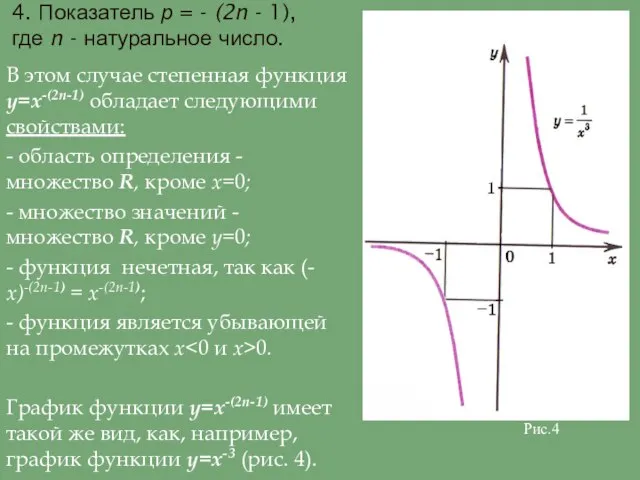
- функция является убывающей на промежутках х<0 и х>0.
График функции y=х-(2n-1) имеет такой же вид, как, например, график функции y=х-3 (рис. 4).
Рис.4
Слайд 85. Показатель р - положительное действительное нецелое число.
В этом случае функция
5. Показатель р - положительное действительное нецелое число.
В этом случае функция

область определения - неотрицательные числа х;
множество значений - неотрицательные числа у;
функция является возрастающей на промежутке (x; ∞).
График функции у=хР, где р - положительное нецелое число, имеет такой же вид, как, например, график функции у=х (при 0<р< 1) или как, например, график функции y=x (при p>1) (рис.5 a, б)
 Сохраняя традиции вкуса, используя уникальные современные технологии, мы создали для Вас столовые приборы, которые сделают Вашу ж
Сохраняя традиции вкуса, используя уникальные современные технологии, мы создали для Вас столовые приборы, которые сделают Вашу ж Технология возведения подземных инженерных сооружений
Технология возведения подземных инженерных сооружений Жан Пиаже
Жан Пиаже Презентация на тему Разработка экспортных и импортных контрактов
Презентация на тему Разработка экспортных и импортных контрактов  ИССЛЕДОВАНИЕ РОЛИ ЭКСПЕРТНОГО СООБЩЕСТВА, СМИ, ОТРАСЛЕВЫХ АССОЦИАЦИЙ, ДРУГИХ ОБЩЕСТВЕННЫХ ОБЪЕДИНЕНИЙ В ОПРЕДЕЛЕНИИ ПРОДОВОЛЬСТ
ИССЛЕДОВАНИЕ РОЛИ ЭКСПЕРТНОГО СООБЩЕСТВА, СМИ, ОТРАСЛЕВЫХ АССОЦИАЦИЙ, ДРУГИХ ОБЩЕСТВЕННЫХ ОБЪЕДИНЕНИЙ В ОПРЕДЕЛЕНИИ ПРОДОВОЛЬСТ PowerPoint Show by Andrew
PowerPoint Show by Andrew СООО ПП Полесье - крупнейший производитель пластмассовых игрушек
СООО ПП Полесье - крупнейший производитель пластмассовых игрушек Портфолио успешной личности (9 КЛАСС)
Портфолио успешной личности (9 КЛАСС) Деятельность ОУ в реализации проекта «Профилактика правонарушений среди несовершеннолетних»
Деятельность ОУ в реализации проекта «Профилактика правонарушений среди несовершеннолетних» Библиотека университета Барселоны
Библиотека университета Барселоны Читаем классику без словаря
Читаем классику без словаря Аттракцион колотушка: маленькое яблоко
Аттракцион колотушка: маленькое яблоко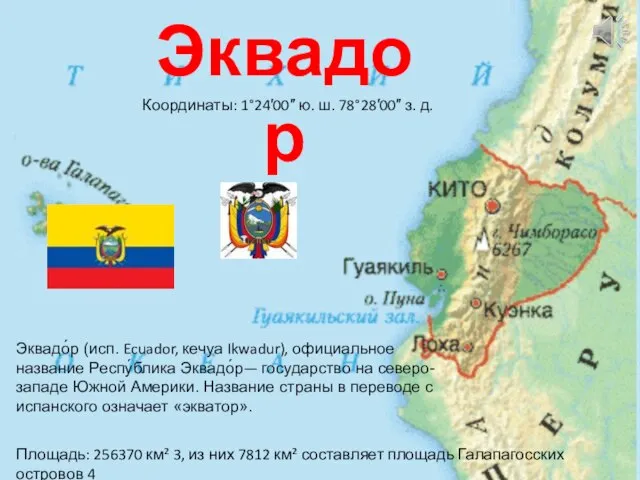 Презентация на тему Эквадор
Презентация на тему Эквадор Рекламная кампания центра дополнительного образования
Рекламная кампания центра дополнительного образования Решение задач на построение сечений..pptx
Решение задач на построение сечений..pptx Образовательная система «ГРАНИ БОГАТСТВА» Чтобы заработать на жизнь, надо работать, но чтобы разбогатеть нужно представить что-то
Образовательная система «ГРАНИ БОГАТСТВА» Чтобы заработать на жизнь, надо работать, но чтобы разбогатеть нужно представить что-то Общественное здоровье
Общественное здоровье Мировой океан проблемы
Мировой океан проблемы Презентация на тему Типы собеседников
Презентация на тему Типы собеседников ПРИСТАВКИ
ПРИСТАВКИ Алканы
Алканы Коррупция как препятствие развития предпринимательской деятельности в регионе
Коррупция как препятствие развития предпринимательской деятельности в регионе Эвакуация населения
Эвакуация населения Внедрение нового формата ведения бизнеса
Внедрение нового формата ведения бизнеса Система работы по выполнению ФЗ № 120 «Об основах системы профилактики правонарушений и безнадзорности несовершеннолетних» в МОУ
Система работы по выполнению ФЗ № 120 «Об основах системы профилактики правонарушений и безнадзорности несовершеннолетних» в МОУ  Пушкин и Тамбовский край
Пушкин и Тамбовский край Подготовка к сочинению в форме эссе "Человек и война" 11 класс
Подготовка к сочинению в форме эссе "Человек и война" 11 класс Публикация материалов в сборнике проектных технологий
Публикация материалов в сборнике проектных технологий