Студийный портрет

Портрет
Портре́т (фр. portrait, от старофранц. portraire — «воспроизводить что-либо черта в черту»1], устар. парсуна — от лат. persona — «личность; особа») — изображение или описание какого-либо человека либо группы людей, существующих или существовавших в реальной действительности[2], в том числе художественными средствами (живописи, графики, гравюры, скульптуры, фотографии, полиграфии), а также в литературе и криминалистике
Фотография человека или группы людей, передающая индивидуальное сходство, раскрывающая внутренний мир и характер, выявляющая в облике типические черты эпохи и социальной среды.

Студийный портрет
Зачем?
Независимость от погоды и времени суток
Абсолютная управление светом для решения любых творческих задач.
Повторяемость светотеневого рисунка.
Большое количество вспомогательных аксессуаров.
Удобство работы с командой (визажист, стилист, декоратор и т.п.)

Типы осветительных приборов
Импульсный свет
Состоит из лампы-
вспышки и
лампы пилотного
света
+
Высокая мощность
Равномерное формирование светового потока
Невысокая теплоотдача
-
Лампа пилотного света не всегда позволяет корректно оценить светотеневой рисунок итогового изображения
Необходимость снимать на закрытой диафрагме (в следствии высокой мощности)
Постоянный свет
Одна
галогеновая
лампы
+
Вы видите светотеневой рисунок сразу «как будет» на фотографии
-
Относительно невысокая мощность
Очень высокая теплоотдача (приборы сильно нагреваются)
На «бюджетных» моделях – неравномерный световой поток (в центре ярче, спад по краям)

Виды освещения (света)
Рисующий свет – основной источник, формирующий светотеневой рисунок
Заполняющий свет – источник, позволяющий снизить общий контраст изображения, сделать тени менее жесткими
Контровой свет – используется для отделения объекта съемки от фона
Моделирующий свет – улучшение передачи объема объекта
Фоновый свет - свет, освещающий фон
2
1
3
4
4
5

Настройки камеры
для импульсного света
Режим съемки: только “M”!
ISO 100. Постоянно, не меняется НИКОГДА
Баланс белого: как правило, «Вспышка»
Выдержка: 1/200 сек. (как правило, иногда 1/125)
Диафрагма: в зависимости от мощности света.
То есть, при съемке с импульсными источниками света управляем двумя параметрами: мощность приборов и диафрагма
НА ПОКАЗАНИЯ ЭКСПОЗАМЕРА ВНИМАНИЯ НЕ ОБРАЩАЕМ!

Синхронизация
В отличие от источников постоянного света, импульсный свет должен сработать именно в тот момент, когда производится снимок, то есть сработать синхронно с затвором камеры. Для синхронизации импульсного света и камеры можно использовать несколько вариантов:
В большинство приборов импульсного света встроен датчик, реагирующий на «резкое» изменение освещенности – так называемая «световая ловушка». Синхронизация с помощью световой ловушки может быть произведена с помощью:
- инфракрасного синхронизатора
- вспышка внешняя (устанавливается на минимальную мощность, направляется В СТОРОНУ от объекта съемки, чтобы не влиять на светотеневой рисунок)
Радиосинхронизация – осуществляется (как правило) с помощью пары приемник-передатчик - на камере передатчик (внешний), в приборе (встроенный или внешний) – приемник
Синхрошнур – прямое соединение камеры и импульсного прибора с помощью специального кабеля (не все камеры имеют выход)
При съемке с несколькими источниками – синхронизируется 1 (один) прибор любым из способов, остальные срабатывают от вспышки этого прибора с помощью «световой ловушки»

Диафрагменные числа
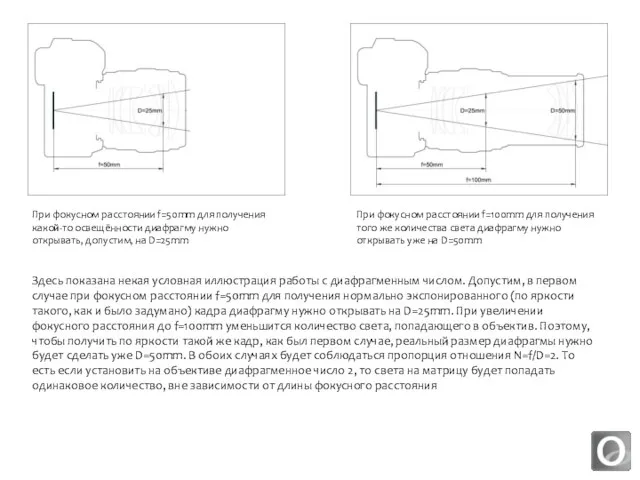
Объектив - устройство довольно сложное и количество света, попадающего в него, как правило, напрямую связано с фокусным расстоянием. То есть, чем больше фокусное расстояние (и чем меньше угол обзора объектива), тем меньше света попадает в объектив. В предельно простой аналогии объектив — это как труба. Меньше фокусное расстояние — труба меньшей длинны, кольцо по сути. Больше фокусное расстояние — труба большей длины. В длинной трубе света меньше, чем в кольце. Это, конечно, предельно упрощённая аналогия, но она отражает положение вещей.
Если бы диафрагма открывалась на заданные величины, измеряемые, допустим, в миллиметрах, то при одинаково открытой диафрагме на объективах с различными фокусными расстояниями получалось бы разное количество света, попадающего внутрь фотоаппарата. И контролировать процесс получения снимка заданной яркости в таких условиях было бы довольно затруднительно: при фиксированной диафрагме (отверстии неизменного диаметра в данном случае) на коротком фокусном расстоянии в объектив попадало бы больше света, чем в объектив с длинным фокусным расстоянием.
Поэтому были придуманы так называемые диафрагменные числа. Диафрагменное число — это дробь, отношение заднего фокусного расстояния объектива к диаметру входного зрачка (изображения диафрагмы, построенного стоящими перед ней линзами в обратном ходе лучей). Если говорить проще — то эти числа (обозначим их здесь буквой N) представляют собой соотношения фокусного расстояния (f) к реальному размеру диафрагмы (D):
Эта странная на первый взгляд вещь сделана для того, чтобы на объективах с разным фокусным расстоянием была возможность получать одинаковое количество света, установив нужное значение диафрагменного числа (N). По сути, диафрагменные числа позволяют проще контролировать процесс съёмки, делая его независимым от фокусного расстояния объективов. Выбрал диафрагменное число и если оно доступно для данной модели объектива, то при изменении фокусного расстояния, количество света, попадающего на матрицу, будет одно и то же:

При фокусном расстоянии f=100mm для получения того же количества света диафрагму нужно открывать уже на D=50mm
При фокусном расстоянии f=50mm для получения какой-то освещённости диафрагму нужно открывать, допустим, на D=25mm
Здесь показана некая условная иллюстрация работы с диафрагменным числом. Допустим, в первом случае при фокусном расстоянии f=50mm для получения нормально экспонированного (по яркости такого, как и было задумано) кадра диафрагму нужно открывать на D=25mm. При увеличении фокусного расстояния до f=100mm уменьшится количество света, попадающего в объектив. Поэтому, чтобы получить по яркости такой же кадр, как был первом случае, реальный размер диафрагмы нужно будет сделать уже D=50mm. В обоих случаях будет соблюдаться пропорция отношения N=f/D=2. То есть если установить на объективе диафрагменное число 2, то света на матрицу будет попадать одинаковое количество, вне зависимости от длины фокусного расстояния

Поскольку диафрагменное число — это результат дроби, то и записывают его в виде 1:1.2, или как дробь с буквой "f": f/5.6 или f/8.
Опять же, поскольку диафрагменное число — это результат дроби, то при понимании работы диафрагмы нужно учитывать обратный эффект: чем меньше диафрагменное число, тем больше света попадает в объектив и наоборот — чем больше это число, тем меньше света будет попадать на матрицу. К примеру, когда диафрагменное число установлено f/1.2, то это будет означать, что диафрагма сильно открыта (и через неё проходит много света). А, допустим, когда диафрагменное число f/22 — это значит, что диафрагма сильно закрыта (и света на матрицу попадать будет мало).
Минимальное диафрагменное число, которое можно выставить на объективе, называется его светосилой. То есть, про показанный выше объектив будут говорить, что у него светосила 1.2. Объективы со светосилой более 2.0 (f/1.8, f/1.4, f/1.2 и так далее) считаются сверхсветосильными (хотя эта классификация и несколько устарела в последнее время). Максимальное диафрагменное число как правило не указывают на самом объективе, эту величину можно узнать в описании объектива.

Ряд диафрагменных чисел
Диафрагменные числа собираются в ряд, где каждое следующее число соответствует увеличению освещённости оптического изображения в два раза:
1 - 1.4 - 2 - 2.8 - 4 - 5.6 - 8 - 11 - 16 - 22 - 32 - 45 - 64
Цифры такие "кривые", потому что яркость изображения определяется количеством света, попавшего в объектив. А оно, в свою очередь, зависит от площади входного отверстия. Площадь отверстия при диафрагменном числе f/1.4 ровно в 2 раза больше площади при f/2. А при f/2 в 2 раза больше, чем при f/2.8, и так далее... А поскольку площадь круга определяется формулой п х R2 ("пи ар квадрат", где R — это радиус круга), то в результирующих коэффициентах будет фигурировать квадратный корень, который и даёт в результате "кривизну" цифр диафрагменного ряда.

Для удобства эти ступени часто разбивают на более мелкие отрезки (с шагом 1/3 ступени), которые вы можете видеть в настройках техники:
1.2 - 1.4 - 1.6 - 1.8 - 2 - 2.2 - 2.5 - 2.8 - 3.2 - 3.5 - 4 - 4.5 - 5.0 - 5.6 - 6.3 - 7.1 - 8 - 9 - 10 - 11 - 13 - 14 - 16 - 18 - 20 - 22 - и так далее.
Яркость от одного диафрагменного числа до другого изменяется ровно на ступень (или f-стоп, англ. — f-stop): каждая ступень отличается от соседней изменением яркости изображения в два раза.

ЖЕСТКИЙ И МЯГКИЙ СВЕТ

ЖЕСТКИЙ СВЕТ
Автор фото: Илья Рашап
Жесткий свет, как правило, образуется от точечного источника и является направленным.
Примерами источников жесткого света могут служить: солнце на ясном небе в полдень, прожектор, студийная вспышка с маленьким рефлектором на большом расстоянии от объекта съемки. Жесткий свет образует резкие и глубокие тени, граница между светом и тенью резкая. Такое освещение, если оно направлено под углом, очень хорошо передает характер поверхности и текстуру, но в то же время сильно подчеркивает морщины или неровности кожи. Портреты с жестким светом как правило получаются драматичными, яркими.

МЯГКИЙ СВЕТ
Фото с занятий по студийному портрету
Изображение, получаемое с помощью источника мягкого света, имеет более протяженные границы переходов из света в тень, то есть более широкие тональные переходы. Такое освещение скрадывает текстуру поверхности, неровности и дефекты кожи на портретном снимке становятся менее заметны. Примерами естественных источников мягкого света являются небо в пасмурную погоду, а также большое окно, в которое не попадают прямые лучи солнца.

Важный момент
Мягкость или жесткость освещения определяется относительным размером источника света в сравнении с объектом съемки, а также расстоянием до объекта съемки. Исходя из этого, источник мягкого света может давать и более жесткое освещение, если увеличить расстояние между ним и объектом съемки настолько, что расстояние будет намного больше, чем размер источника. Тогда источник станет близок к точечному.

КОРОТКИЙ И ДЛИННЫЙ СВЕТ

Короткий свет (узкий свет)
Источник освещает сторону лица, расположенную дальше от камеры (предполагается, что лицо повернуто немного в сторону). Прибор ставят так, чтобы он находился немного сзади и сбоку плоскости продольной симметрии лица, которая обозначена красной линией.
Тень при этом ложится на сторону лица, ближнюю к камере. В результате лицо кажется более узким.

Длинный свет (широкий свет)
Если расположить свет так, чтобы он освещал сторону лица, ближнюю к камере, то такой свет будет называться длинным. На схеме ниже показано расположение источника для получения эффекта длинного света.
Тень при этом ложится на сторону лица, дальнюю от камеры. В результате лицо кажется более широким.

СВЕТОФОРМИРУЮЩИЕ НАСАДКИ

Зонт
Зонт на отражение
Часто применяется для создания
заполняющего света или освещения фона
Зонты дают мягкий ровный свет, при этом размером светового пятна можно управлять с помощью изменения расстояния от поверхности зонта до лампы светильника.

Зонт
Просветный зонт (зонт на просвет)
Используется как рисующий свет
Зонты дают мягкий ровный свет, при этом размером светового пятна можно управлять с помощью изменения расстояния от поверхности зонта до лампы светильника.

Два источника освещения с зонтами

Софт-бокс
Насадка большой площади для формирования мягкого света
Разделяют софт-боксы, стрип-боксы, окто-боксы

Софт-рефлектор (портретная тарелка, бьют-диш)
Обеспечивает равномерное распределение света с высокой светоотдачей. Более жесткий свет, чем от софт-бокса.
На примере: дополнительно использовался заполняющий свет

Дополнительно
Отражатель – используется в качестве мягкого пассивного источника света, отражающего свет от активного источника света.
Шторки – для ограничения светового потока
Соты – получение более направленного светового потока

СХЕМЫ СВЕТА

Боковое освещение
Боковой свет разбивает лицо на две равные части, одна из которых освещена, а другая находится в тени. Он часто используется для создания драматических портретов, таких как портрет музыканта или художника. Такой свет больше подходит для мужских портретов и, как правило, для женских применяется редко.
Для достижения эффекта бокового света нужно просто поставить источник света под углом 90 градусов слева или справа от модели, иногда даже чуть позади головы. Размещение и положение источника света будет зависеть от лица человека. Смотрите, как свет ложится на лицо, и передвигайте источник. При правильной постановке бокового света в глазу на теневой стороне лица должен быть блик. Если при этом не удается избавиться от попадания света на щеку, вполне возможно, что данный тип лица не подходит для бокового света.

Петлевое освещение
Петлевое освещение создает небольшую тень от носа на щеке. Чтобы получить такое освещение, нужно поставить источник немного выше уровня глаз и под углом 30-45 градусов от камеры.
В петлевой схеме тень от носа не должна слишком заходить на щеку, тем более не должна смыкаться с тенью от скулы.

Рембрантовская схема света
Рембрандтовское освещение определяется наличием светового треугольника на щеке. В отличие от петлевого света, где тень от носа и щеки не смыкается, здесь они сливаются вместе, что и создает на теневой стороне светлый треугольник на щеке под глазом. Для создания правильной схемы следует убедиться, что в глазу на теневой стороне присутствует блик от источника света, иначе глаза будут "мертвыми", без приятного блеска. Рембрандтовское освещение более драматично, так как подобный светотеневой рисунок создает более беспокойное настроение портрета. Используйте его соответствующим образом.
Для создания рембрандтовского освещения необходимо, чтобы модель находилась немного в стороне от света. Источник должен находиться выше верхней части головы так, чтобы тень от носа падала на щеку. Не каждое лицо подходит для этой схемы. Если оно имеет высокие или выдающиеся скулы, возможно, схема будет работать. Если же у модели маленький нос или плоская переносица, такого освещения может быть трудно достичь. Опять же, помните, что вы не должны делать именно эту схему именно с этой моделью.

«Бабочка»
Эта схема метко названа "бабочкой" по форме тени от носа, которая создается. если источник света поместить сверху и прямо за камерой. В основном при этой схеме фотограф находится под источником света. Схема "бабочка" часто используется для съемки гламура, выгодно подчеркивая скулы модели. Также она походит для съемки людей старшего возраста, так как в отличие от других схем меньше подчеркивает морщины.
Схема "бабочка" создается источником света прямо за камерой и немного выше глаз или головы, в зависимости от типа лица. Иногда схему дополняют отражателем прямо под подбородком, модель даже может держать его сама. Эта схема подходит моделям с красивыми скулами и узким лицом.

СООТНОШЕНИЕ ОСВЕЩЕННОСТИ

1:1
1:1 это равномерное освещение. Здесь нет никакой разницы в освещенности одной и другой стороны лица. Это очень плоское освещение, которое может быть достигнуто различными способами. Во-первых, вы можете использовать заполняющую вспышку и сделать ее мощность равной мощности основного источника света или света от окна. Это довольно трудно достичь, не имея некоторой практики, возможно, вы часто будете перебивать вспышкой естественный свет. Во-вторых, можно использовать отражатель. Он должен находиться очень близко к объекту, чтобы хорошо заполнить тени. Соотношение 1:1 очень легко распознать визуально

2:1
Как можно судить из цифр, при этом соотношении один источник вдвое мощнее другого. Таким образом, зная, что такое ступени экспозиции или f-стопы, мы можем установить это значение освещенности.

4:1
Соотношение 4:1 в два раза больше предыдущего. Итак, если в случае соотношения 2:1 разница была в одну ступень, то сколько будет теперь? В этом случае разница составит 2 ступени, то есть 2х2 = в 4 раза. Разница между освещенной и теневой стороной будет в 2 ступени экспозиции.

8:1
на освещенную сторону попадает в 8 раз больше света, чем на теневую. Это соответствует 3 ступеням экспозиции. Это довольно драматическое освещение, и дальнейшее увеличение соотношения сверх 8:1 приведет к тому, что информация в тенях станет пропадать. Печать имеет максимальный диапазон контрастности примерно 4-6 ступеней, так что если вы не хотите получить чисто белую освещенную и чисто черную теневую стороны, советую использовать соотношение не более 8:1.
Могут возникнуть некоторые трудности при создании такого соотношения. Возможно, потребуется более жесткий источник света или черный отражатель для поглощения света на теневой стороне. Процесс вычисления такой же, как и раньше. Если в соотношении 4:1 разница составляет 2 ступени, то при соотношении 8:1 разница составит 3 ступени. Поэтому, если на освещенной стороне флэшметр показывает диафрагму f/8, то на теневой стороне она должна быть f/8> f/5.6> f/4> f/2.8.

Некоторые рекомендациии:
Для младенцев и маленьких детей используйте 1:1 или 2:1. Это вызвано отчасти и тем, что дети очень подвижны, поэтому трудно выдержать нужное направление света при больших соотношениях. Использование более низкого контраста позволяет большую свободу движения.
Для женщин используйте соотношения 2:1 или 3:1
Для мужских или бизнес-портретов используйте 4:1 или 6:1 (2,5 ступени)
Если вы хотите сделать драматичный снимок, используйте более высокие коэфициенты.