Содержание
- 2. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Классическая теория поля рассматривает физические поля как абстрактные математические функции,
- 3. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Согласно полевой физике объекты не создают поля и не действуют
- 4. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Возмущение полевой среды объектами и передача возмущений полевой среды объектам
- 5. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Полевая среда описывается функцией плотности W(r, t) , которая позволяет
- 6. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru В самом элементарном случае (взаимодействие только двух объектов) функция плотности
- 7. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Реализация указанного механизма полевого взаимодействия двух объектов приводит к Полевому
- 8. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Из полевого уравнению движения следуют: Формула полевой массы m и
- 9. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru В наиболее простом случае функция полевой связи W(R) удовлетворяет уравнению
- 10. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru В полевой физике равноправным образом возникает как электрический заряд qe,
- 11. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru В земных условиях вклад в инертную массу гравитационного поля несоизмеримо
- 12. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Для описания движения в реальных условиях в полевом уравнении движения
- 13. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Классическая механика: Условия: Wg = const Wg >> Wl
- 14. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Релятивистская механика: Условия: Wg = const W = Wg +
- 15. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Галактическое движение: Условия: Wg ≠ const Wg >> Wl
- 16. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Принцип инерции Галилея: При отсутствии внешних сил тело сохраняет состояние
- 17. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Следствия ПФ в космологии: − Объяснение структуры нашей Галактики, в
- 18. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Другие следствия Полевой физики: − Механизм возникновения ядерных сил как
- 19. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Обобщенное полевое уравнение движения: u – скорость исследуемого объекта vk
- 20. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Обобщенное полевое уравнение движения справедливо в совершенно любой СО Совокупность
- 21. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Модель инерциальной СО является частным случаем, справедливым только тогда, когда
- 22. © Репченко Олег Николаевич, 2005, www.fieldphysics.ru Из обобщенного уравнения движения следует скорректированное выражение для силы взаимодействия
- 24. Скачать презентацию





















 В мире амфибий и рептилий
В мире амфибий и рептилий Пешеходный туризм. Часть 2 ( треккинг)
Пешеходный туризм. Часть 2 ( треккинг) Математический диктант 1 класс
Математический диктант 1 класс Predpriatia_obschestvennogo_pitania
Predpriatia_obschestvennogo_pitania Оценка и повышение уровня знаний
Оценка и повышение уровня знаний Плотность вещества, масса и объем. Решение задач
Плотность вещества, масса и объем. Решение задач АСУ ProCollege. Направления работы
АСУ ProCollege. Направления работы День матери 29 ноября
День матери 29 ноября Архитектура XVII столетия
Архитектура XVII столетия Презентация на тему Устное народное творчество
Презентация на тему Устное народное творчество  Поэзии прекрасные страницы
Поэзии прекрасные страницы Божья верность
Божья верность 20140330_rodnik_ayuka
20140330_rodnik_ayuka Презентация на тему: «Биография Александра Исаевича Солженицына»
Презентация на тему: «Биография Александра Исаевича Солженицына»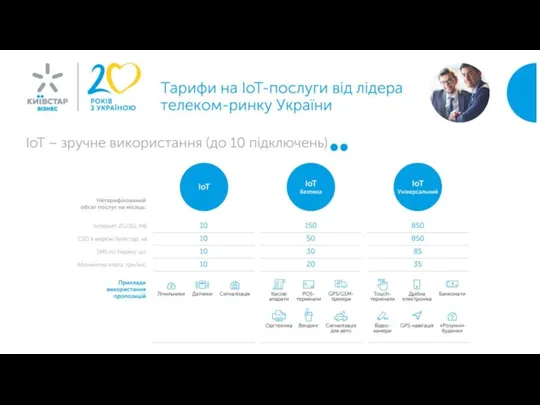 Тарифи на IoT-послуги від лідера телеком-ринку України
Тарифи на IoT-послуги від лідера телеком-ринку України Асимметрия головного мозга
Асимметрия головного мозга Внедрение новых моделей профессиональной ориентации и допрофессиональной подготовки детей с ограниченными возможностями здоров
Внедрение новых моделей профессиональной ориентации и допрофессиональной подготовки детей с ограниченными возможностями здоров Технологический процесс проведения ремонта дефектных участков МН методом установки ремонтніх конструкций
Технологический процесс проведения ремонта дефектных участков МН методом установки ремонтніх конструкций Обществознание 7 класс урок 5 29.2022
Обществознание 7 класс урок 5 29.2022 Макроэкономические регионы мира Катар
Макроэкономические регионы мира Катар Особенности социокультурной деятельности отдела литературы по искусству. Традиции и новации
Особенности социокультурной деятельности отдела литературы по искусству. Традиции и новации Порядок инвентаризации счета 98
Порядок инвентаризации счета 98 ЭПИФИЗ – орган-мишень биотропного действия естественных магнитных волн
ЭПИФИЗ – орган-мишень биотропного действия естественных магнитных волн Оксиды
Оксиды ОПЫТ ПРОВЕДЕНИЯ IPO ОАО «ПЛАТФОРМА ЮТИНЕТ.РУ» на РИИ ММВБ
ОПЫТ ПРОВЕДЕНИЯ IPO ОАО «ПЛАТФОРМА ЮТИНЕТ.РУ» на РИИ ММВБ Исторические события 5 класс
Исторические события 5 класс Белки – это жизнь?
Белки – это жизнь?