Слайд 2 «Пусть кто-нибудь попробует вычеркнуть из математики степени,
и он увидит, что

без них далеко не уедешь»
М.В. Ломоносов
Слайд 3Определение степени с натуральным показателем
Степенью числа а с натуральным показателем п,

большим 1, называется выражение, равное произведению п множителей, каждый из которых равен а.
Слайд 4Определение степени с натуральным показателем

Слайд 5Свойства степени
При умножении степеней с одинаковыми основаниями основание оставляют прежним, а

показатели степеней складывают
При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя
При возведении степени в степень основание оставляют тем же, а показатели перемножают
При возведении в степень произведения возводят в эту степень каждый множитель и результаты перемножают
При возведении дроби в степень в эту степень возводят числитель и знаменатель и результаты делят.





 Тревожные дети
Тревожные дети Специальные захваты грузоподъёмных машин
Специальные захваты грузоподъёмных машин ООО Название компании. Шаблон презентации
ООО Название компании. Шаблон презентации Окружность, круг
Окружность, круг Влияние каллиграфии на мозговую активность. 3 часть
Влияние каллиграфии на мозговую активность. 3 часть Законодательствов области обращенияс опасными отходами
Законодательствов области обращенияс опасными отходами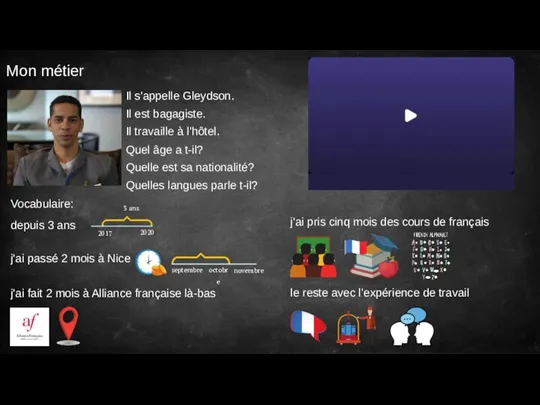 Mon métier
Mon métier КУЛЬТУРА ЗАПАДНОЕВРОПЕЙСКОГОСРЕДНЕВЕКОВЬЯ
КУЛЬТУРА ЗАПАДНОЕВРОПЕЙСКОГОСРЕДНЕВЕКОВЬЯ Спортивный коллектив
Спортивный коллектив Приемы сжатия текста
Приемы сжатия текста презент орелй
презент орелй Організація дистанційного навчання, за допомогою платформи MOODLE
Організація дистанційного навчання, за допомогою платформи MOODLE Метод полуреакций или электронно-ионного баланса
Метод полуреакций или электронно-ионного баланса Дистанционное обучение
Дистанционное обучение Перспективы развития платежной системы Банка России в свете Федерального закона «О национальной платежной системе»
Перспективы развития платежной системы Банка России в свете Федерального закона «О национальной платежной системе» Used Car Market in India – A Quikr Review
Used Car Market in India – A Quikr Review Биография и творчество А. А. Вознесенского
Биография и творчество А. А. Вознесенского ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования «МОСКОВ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования «МОСКОВ Смерть и оживление
Смерть и оживление Аренда земельных участков
Аренда земельных участков Презентация на тему Таможня в 21-ом веке
Презентация на тему Таможня в 21-ом веке Динамика уровня экономического и социального развития Санкт-Петербурга
Динамика уровня экономического и социального развития Санкт-Петербурга 2
2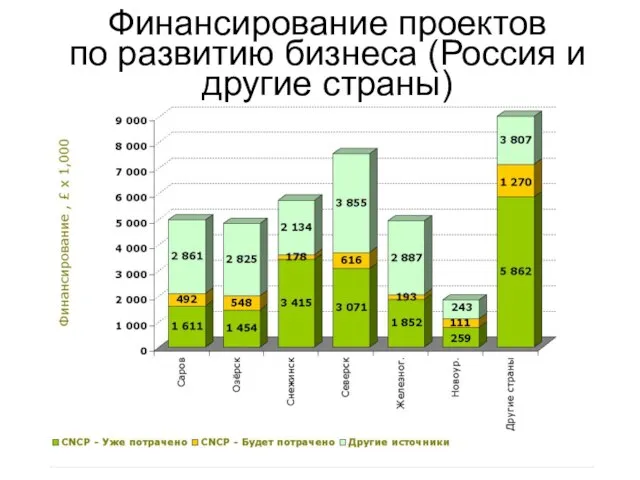 Финансирование проектов по развитию бизнеса (Россия и другие страны)
Финансирование проектов по развитию бизнеса (Россия и другие страны) ??????? ????????????????
??????? ???????????????? Рациональные уравнения
Рациональные уравнения Russian Fashion Retail Forum
Russian Fashion Retail Forum Применение жиров
Применение жиров