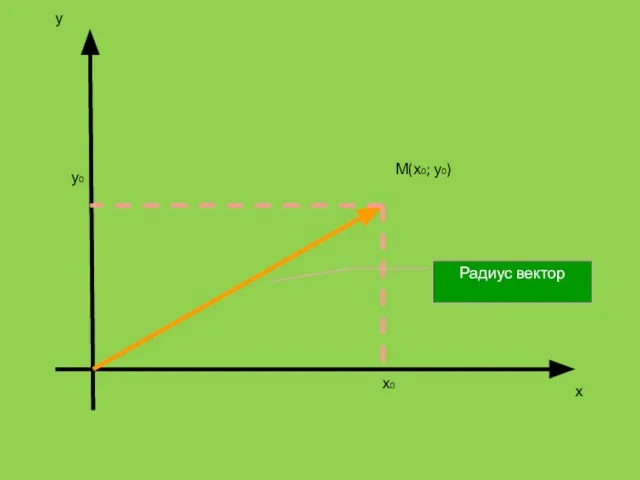
Слайд 2М(х0; у0)
х0
у0
у
х
Радиус вектор
Слайд 3х
у
1
5
3
2
0
1
5
4
3
2
6
6
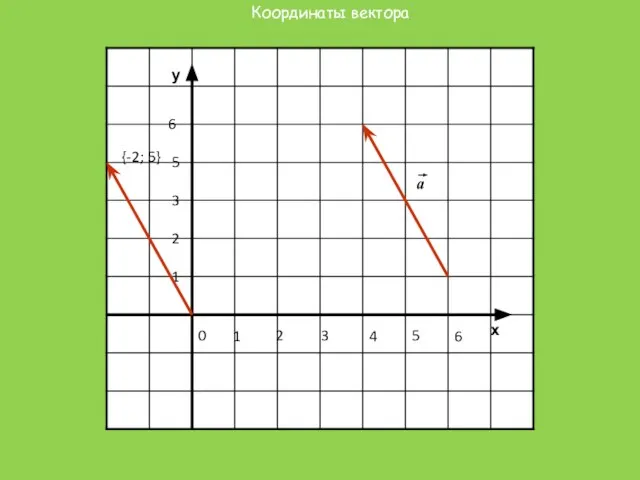
Координаты вектора
{-2; 5}
a
Слайд 4х
у
1
5
3
2
0
1
5
4
3
2
6
6
Координаты вектора
В(х2; у2)
А(х1; у1)
АВ=ОВ-ОА
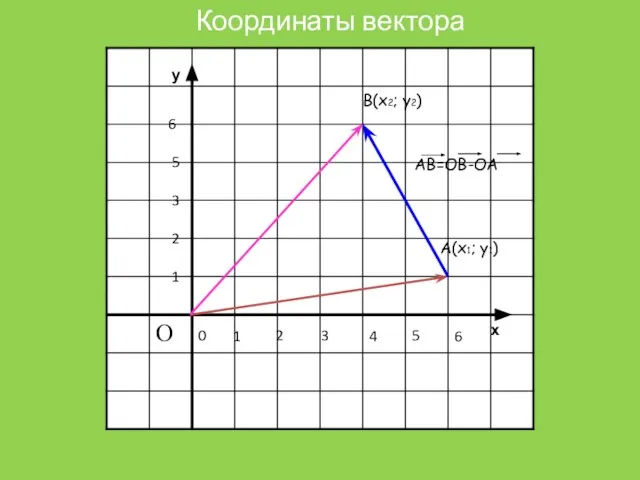
Слайд 5Каждая координата вектора равна разности соответствующих координат его конца и начала
Даны точки

А(х1; у1) и В(х2; у2), тогда
Координаты вектора АВ{х2 – х1; у2 – у1}
Слайд 6Простейшие
задачи
в координатах

Слайд 7х
у
1
5
3
2
0
1
5
4
3
2
6
6
Координаты середины отрезка
В(х2; у2)
А(х1; у1)
ОС=1/2(ОВ-ОА)
С
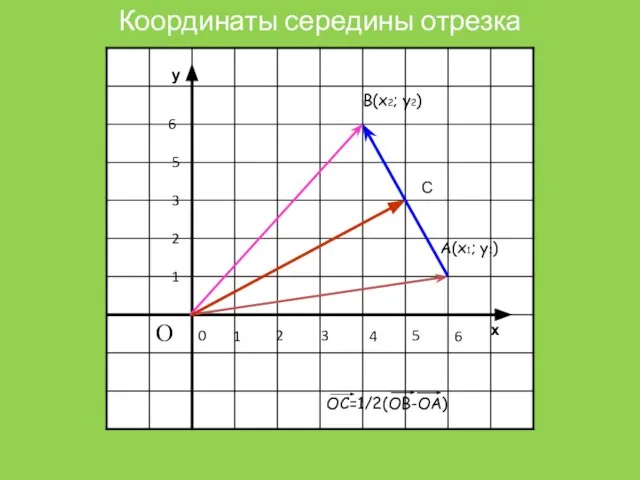
Слайд 8Каждая координата средины отрезка равна полусумме соответствующих координат его концов

Слайд 9х
у
1
5
3
2
0
1
5
4
3
2
6
6
Длина вектора
А(х; у)
а
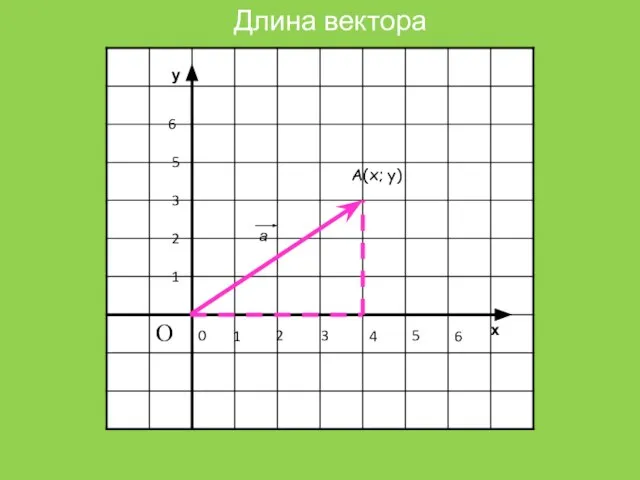
Слайд 10Длина вектора вычисляется по формуле










 Проектирование полуботинок с настрочными берцами
Проектирование полуботинок с настрочными берцами Бюджет для граждан на 2022 год
Бюджет для граждан на 2022 год Ластоногие и Китообразные, Парнокопытные и Непарнокопытные, Хоботные
Ластоногие и Китообразные, Парнокопытные и Непарнокопытные, Хоботные РЕЗУЛЬТАТЫ РАБОТЫПОДСИСТЕМЫ «ВЕДЕНИЯ»
РЕЗУЛЬТАТЫ РАБОТЫПОДСИСТЕМЫ «ВЕДЕНИЯ» Переход к предоставлению услуги «Социальная поддержка ветеранов труда, лиц, проработавших в тылу в период Великой Отечественной в
Переход к предоставлению услуги «Социальная поддержка ветеранов труда, лиц, проработавших в тылу в период Великой Отечественной в Ивановское сельское поселение. Исполнение бюджета
Ивановское сельское поселение. Исполнение бюджета О компании Jura Elektroapparate AG
О компании Jura Elektroapparate AG The flag of the uk
The flag of the uk Желаем Вам приятного просмотра! Для смены слайдов нажимайте клавишу ПРОБЕЛ.
Желаем Вам приятного просмотра! Для смены слайдов нажимайте клавишу ПРОБЕЛ. На пути к Библиотеке 2.0: освоение перспективных интернет-технологий
На пути к Библиотеке 2.0: освоение перспективных интернет-технологий Расчёт на прочность при изгибе
Расчёт на прочность при изгибе Видеонаблюдение при проведении выборов депутатов Государственной Думы
Видеонаблюдение при проведении выборов депутатов Государственной Думы В царстве грибов
В царстве грибов Бизнес планирование предприятий
Бизнес планирование предприятий План мероприятий на каникулы
План мероприятий на каникулы Н. В. Гоголь в разделе «Что такое слово и словесность» пишет: "Говорится все, записывается немногое, и только то, что нужно. Отсюда зн
Н. В. Гоголь в разделе «Что такое слово и словесность» пишет: "Говорится все, записывается немногое, и только то, что нужно. Отсюда зн Значение природных ресурсов
Значение природных ресурсов Презентация 6-7 СРО Шевченко Д.В
Презентация 6-7 СРО Шевченко Д.В Как выполняли арифметические действия в Древнем Риме?
Как выполняли арифметические действия в Древнем Риме? Мастер-класс
Мастер-класс Презентация на тему: Проблемы подросткового возраста и его особенности
Презентация на тему: Проблемы подросткового возраста и его особенности Телекоммуникации
Телекоммуникации Сварные соединения и швы
Сварные соединения и швы Цапина Елена Михайловна Классный руководитель6 «а» класса Школа №9 г.Можга
Цапина Елена Михайловна Классный руководитель6 «а» класса Школа №9 г.Можга Презентация на тему Обучение грамоте и развитие речи
Презентация на тему Обучение грамоте и развитие речи Les meilleures montres dans le monde
Les meilleures montres dans le monde Презентация на тему Открытия Ломоносова в области физики
Презентация на тему Открытия Ломоносова в области физики  Маньяки… кто есть кто
Маньяки… кто есть кто