ТЕЧЕНИЕ И СВОЙСТВА ЖИДКОСТЕЙ

Течение жидкости изображается линиями тока — линиями, касательные к которым в каждой точке совпадают с направлением вектора скорости частиц. Течение жидкости называется установившемся, стационарным, если скорости частиц в каждой точке потока со временем не изменяются (при этом условии линии тока совпадают с траекториями частиц жидкости).

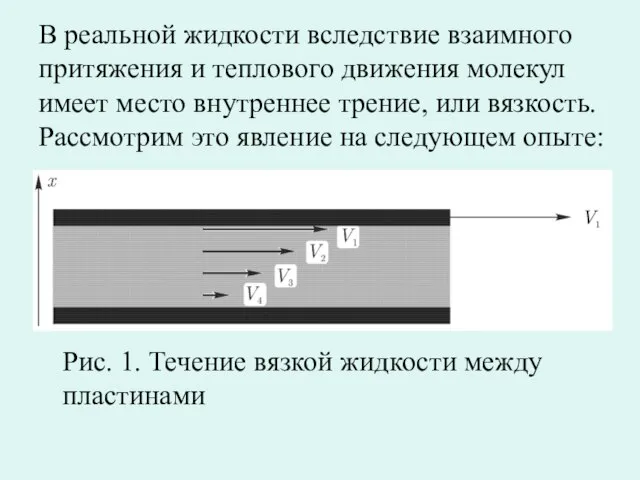
В реальной жидкости вследствие взаимного притяжения и теплового движения молекул имеет место внутреннее трение, или вязкость. Рассмотрим это явление на следующем опыте:
Рис. 1. Течение вязкой жидкости между пластинами

Силы, действующие между слоями, направленные по касательной к поверхности слоев, называются силами внутреннего трения, или вязкости. Эти силы пропорциональны площади взаимодействующих слоев S и тем больше, чем больше их относительная скорость.

Силы внутреннего трения подчиняются уравнению Ньютона:
(1)
где ось х перпендикулярна направлению движения слоев жидкости; η — коэффициент внутреннего трения, или динамическая вязкость (размерность η в СИ — [Па · с]); dV/dx — градиент скорости (grad V), показывающий изменение скорости, в направлении х.

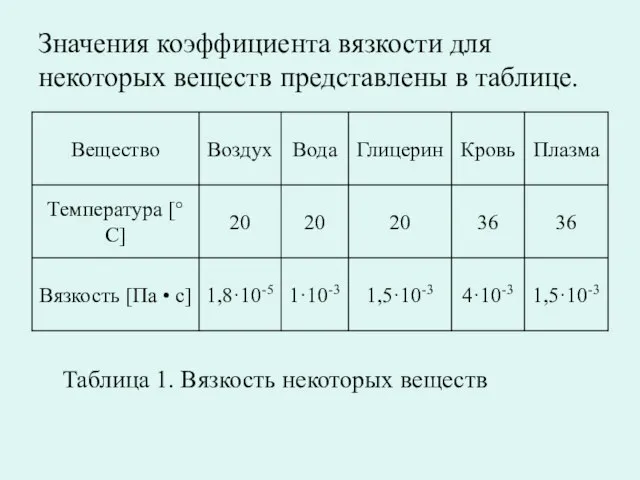
Значения коэффициента вязкости для некоторых веществ представлены в таблице.
Таблица 1. Вязкость некоторых веществ

Ньютоновские и неньютоновские жидкости
Ньютоновские жидкости — такие, для которых вязкость не зависит от градиента скорости, они подчиняются уравнению Ньютона. К ним относят воду, водные растворы, низкомолекулярные органические жидкости (этиловый спирт, ацетон).

Неньютоновские жидкости — такие, для которых вязкость зависит от режима течения и градиента скорости. К ним относят высокомолекулярные органические соединения, суспензии, эмульсии. Это жидкости состоят из сложных и крупных молекул.

Ламинарное и турбулентное течение
При течении однородной жидкости по сосуду в ней можно выделить несколько слоев.
Ламинарное (слоистое) течение — такое, при котором слои жидкости текут, не перемешиваясь, скользя друг относительно друга. Ламинарное течение — это плавное, медленное, упорядоченное, регулярное течение жидкости.

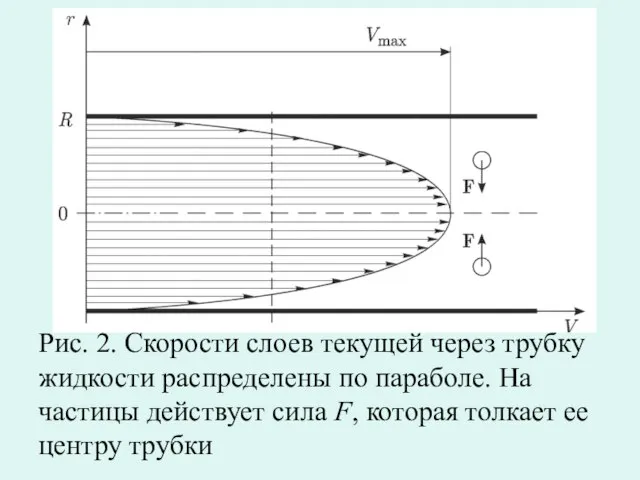
Течение крови в артериях в норме является ламинарным. Вследствие симметрии ясно, что в трубе, при ламинарном течении, частицы жидкости, равноудаленные от оси, имеют одинаковую скорость.
(2)

Рис. 2. Скорости слоев текущей через трубку жидкости распределены по параболе. На частицы действует сила F, которая толкает ее центру трубки

Турбулентное (вихревое) течение — такое течение, при котором скорости частиц жидкости в каждой точке непрерывно меняются, приходят в колебательное движение, которое сопровождается появлением звука.

Турбулентное течение — это хаотическое, крайне нерегулярное, неупорядоченное течение жидкости. Элементы жидкости совершают движение по сложным неупорядоченным траекториям, что приводит к перемешиванию между слоями жидкости и к образованию местных завихрений.

Число Рейнольдса
Экспериментально показано, что турбулентность возникает, когда определенная комбинация величин, характеризующих движение, превосходит некоторое критическое значение.
Число Рейнольдса определяется по формуле (3)

Формула Пуазейля
При ламинарном течении жидкости по трубе радиусом R и длиной L объем Q жидкости, протекающей через горизонтальную трубу за одну секунду, можно вычислить следующим образом.
(4)

Формулу Пуазейля можно записать в виде, справедливом для труб переменного сечения. Заменим отношение (P1 - Р2)/ L на градиент давления dP/dl, тогда получим
(5)

Проведем аналогию между формулой Пуазейля и формулой закона Ома для участка цепи без источника тока: I = ΔU/R. Для этого перепишем формулу (4) в следующем виде:
Величина X называется гидравлическим сопротивлением:
(6)

Методы определения вязкости жидкостей
Совокупность методов измерения вязкости жидкости называется вискозиметрией. Прибор для измерения вязкости называется вискозиметром.
В зависимости метода измерения вязкости используют следующие типы вискозиметров.

а) Капиллярный вискозиметр Оствальда основан на использовании формулы Пуазейля. Вязкость определяется по результату измерения времени протекания через капилляр жидкости известной массы под действием силы тяжести при определенном перепаде давлений.

б) Медицинский вискозиметр Гесса с двумя капиллярами, в которых движутся две жидкости (например, дистиллированная вода и кровь). Вязкость одной жидкости должна быть известна. Учитывая, что перемещение жидкостей за одно и то же время обратно пропорционально их вязкости вычисляют вязкость второй жидкости.

в) Вискозиметр, основанный на методе Стокса, согласно которому при движении шарика в вязкой жидкости с небольшой скоростью сила сопротивления пропорциональна вязкости этой жидкости.

г) Вискозиметр ротационный, в котором вязкость измеряется по угловой скорости ротора, подвижного цилиндра в системе двух соосных цилиндров, в зазоре между которыми находится жидкость. Данный вискозиметр позволяет измерять вязкость при разных угловых скоростях вращения ротора, что в свою очередь позволяет установить зависимость между вязкостью и градиентом скорости, что важно для неньютоновских жидкостей.

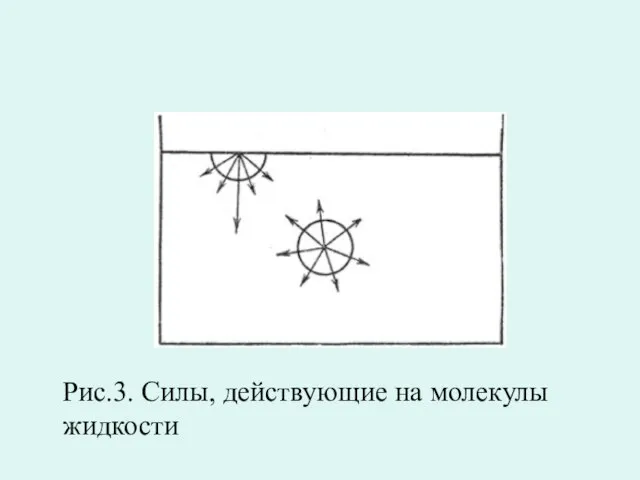
Поверхностное натяжение
Молекула, находящаяся внутри жидкости взаимодействует с соседними молекулами окружающими ее и, равнодействующая сила, которая на нее действует, равна нулю.
Молекулы поверхностного слоя находятся при других условиях. На каждую молекулу поверхностного слоя действует равнодействующая сила, направленная по нормали внутрь жидкости

Рис.3. Силы, действующие на молекулы жидкости

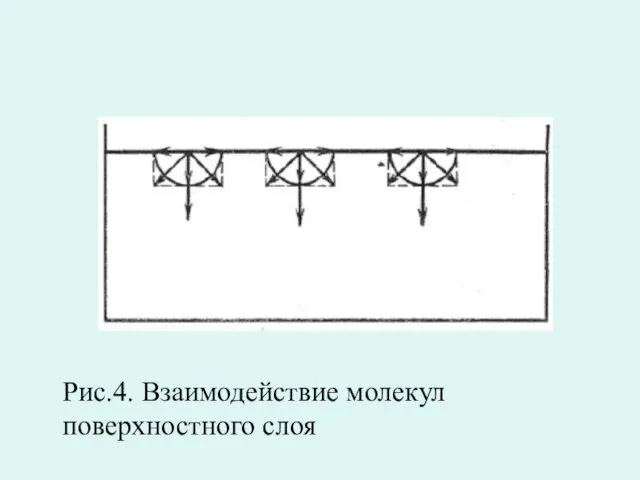
Рис.4. Взаимодействие молекул поверхностного слоя

Межмолекулярное взаимодействие создает силы направленные по касательной к поверхности жидкости и стремящиеся сократить поверхность жидкости. Если на поверхности жидкости провести произвольную линию, то по нормали к линии и по касательной к поверхности будут действовать силы поверхностного натяжения.

Величина этих сил пропорциональна числу молекул, находящихся вдоль этой линии, следовательно, пропорциональна длине линии:
F = σl (7)
где σ – коэффициент пропорциональности, который называется коэффициентом поверхностного натяжения

Коэффициент поверхностного натяжения численно равен силе поверхностного натяжения, действующей на единицу длины контура, ограничивающего поверхность жидкости.
[Н/м] (8)

Величина σ зависит от рода жидкости, температуры, наличия примесей. Вещества, которые уменьшают поверхностное натяжение, называются поверхностно – активными или ПАВ (спирт, мыло, стиральный порошок и т.д.). Вещества, которые увеличивают поверхностное натяжение, называются поверхностно – инактивными или ПИВ (глюкоза).

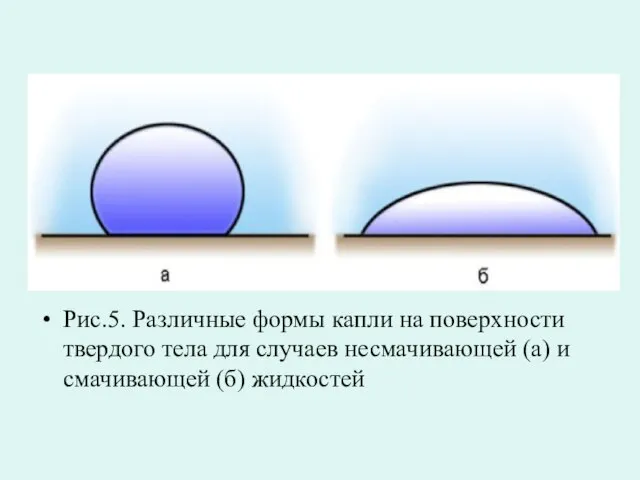
Капиллярные явления
Если при контакте жидкости и твердого тела взаимодействие между их молекулами более сильное, чем взаимодействие между молекулами самой жидкости, то жидкость стремится увеличить поверхность соприкосновения и растекается по поверхности твердого тела. В этом случае жидкость смачивает твердое тело.

Если взаимодействие между молекулами жидкости сильнее, чем взаимодействие между молекулами жидкости и твердого тела, то жидкость сокращает поверхность соприкосновения. В этом случае жидкость не смачивает твердое тело.

Рис.5. Различные формы капли на поверхности твердого тела для случаев несмачивающей (а) и смачивающей (б) жидкостей

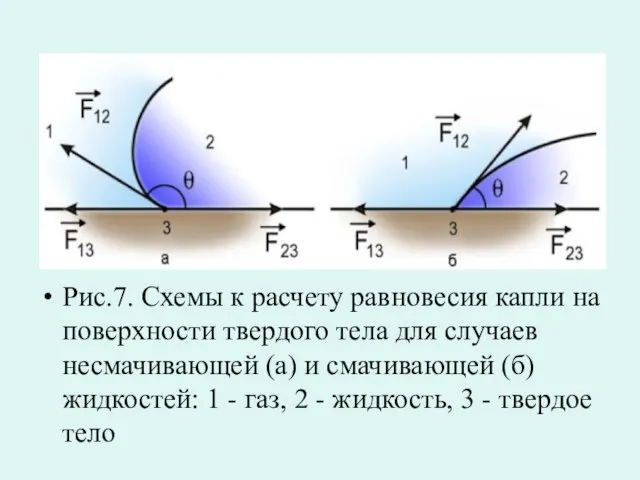
Рис.7. Схемы к расчету равновесия капли на поверхности твердого тела для случаев несмачивающей (а) и смачивающей (б) жидкостей: 1 - газ, 2 - жидкость, 3 - твердое тело

Рассмотрим случай когда:σ23 = σ12 + σ13
Это значит, что ∠θ = π (рис.7,а). Окружность, которая ограничивает место соприкосновения жидкости с твердым телом, будет стягиваться в точку и капля принимает эллипсоидальную или сферическую форму. Это случай полного несмачивания. Полное несмачивание наблюдается также и в случае:
σ23 > σ12 + σ13.

Другой граничный случай будет наблюдаться если: σ13 = σ12 + σ23
Это значит, что ∠θ = 0 (рис.7,б), наблюдается полное смачивание. Полное смачивание будет наблюдаться и в случае когда: σ13 > σ12 + σ23.
В этом случае равновесия не будет, ни при каких значениях угла θ, и жидкость будет растекаться по поверхности твердого тела вплоть до мономолекулярного слоя.

Угол между касательными к поверхности твердого тела и к поверхности жидкости, который отсчитывается внутри жидкости, называется краевым углом. Его значение определяется :
(7)

Если σ13 > σ23, то cosθ > 0, угол θ острый – имеет место частичное смачивание, если σ13 < σ23, то cosθ < 0 – угол θ тупой – имеет место частичное несмачивание.

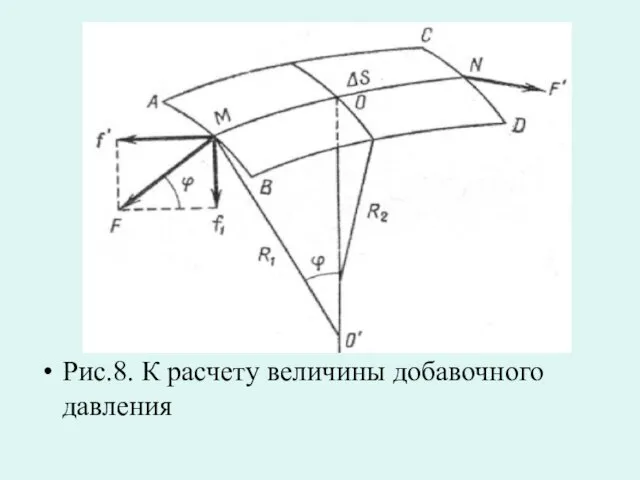
Кривизна поверхности жидкости приводит к возникновению добавочного давления, действующего на жидкость под этой поверхностью.
Добавочное давление, которое оказывает искривленная поверхность жидкости на внутренние области жидкости, называется лапласовым давлением.

Рис.8. К расчету величины добавочного давления

(8)
Уравнение (8) называется формулой Лапласа.
Лапласовское давление очевидно направлено к центру кривизны поверхности.

В случае выпуклой поверхности оно направлено внутрь жидкости и добавляется к нормальному давлению жидкости. В случае вогнутой поверхности жидкость будет находиться под меньшим давлением, чем жидкость под плоской поверхностью, т.к. лапласовское давление направлено за пределы жидкости.

Если поверхность сферическая, то:
R1 = R2 = R:
Если поверхность цилиндрическая, то:
R1 = R, R2 = ∞:
Если поверхность плоская то:
R1 = ∞, R2 = ∞:

С явлениями смачивания и несмачивания связаны так называемые капиллярные явления. Если в жидкость опустить капилляр (трубка малого диаметра), то поверхность жидкости в капилляре принимает вогнутую форму, близкую к сферической в случае смачивания и выпуклую в случае несмачивания. Такие поверхности называются менисками.

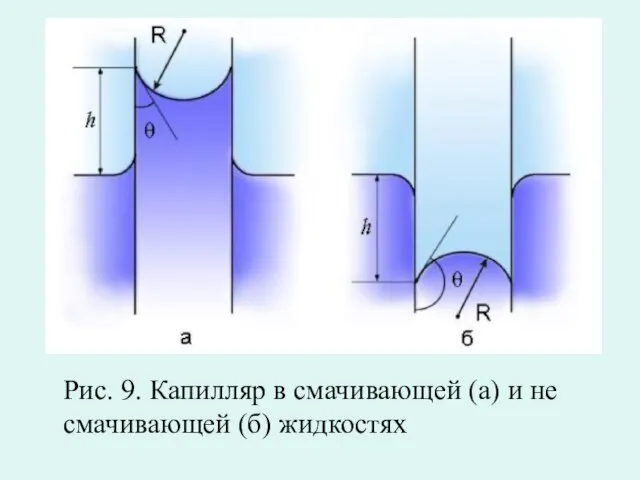
Рис. 9. Капилляр в смачивающей (а) и не смачивающей (б) жидкостях

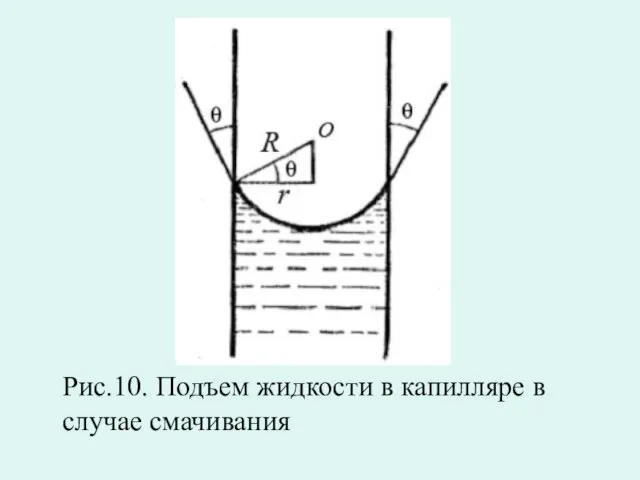
Рис.10. Подъем жидкости в капилляре в случае смачивания

В случае вогнутого мениска добавочное давление направленно к центру кривизны вне жидкости. Поэтому давление под мениском меньше давления под плоской поверхностью жидкости в сосуде на величину лапласова давления:
где (9)

Следовательно, лапласово давление вызовет подъем жидкости в капилляре на такую высоту h (рис.9), пока гидростатическое давление столба жидкости не уравновесит лапласово давление: (10)