Содержание
- 2. Анализ оптимального плана 1. Эффективные и неэффективные ограничения ♦ max 800·x1 + 950·x2 + 4200·x3 (руб./сут.)
- 3. Анализ оптимального плана 1. Эффективные и неэффективные ограничения: экономические резервы ♦ Разница между свободным членом и
- 4. Анализ оптимального плана 1. Эффективные и неэффективные ограничения: экономические резервы Разница между свободным членом и суммой
- 5. Анализ оптимального плана 1. Эффективные и неэффективные ограничения: оценка адекватности модели Действительно ли избыточные ресурсы не
- 6. Анализ оптимального плана 2. Двойственные оценки ♦ Рассмотрим задачу с точки зрения возможного изменения её параметров
- 7. Анализ оптимального плана 2. Двойственные оценки Для эффективного ограничения отлична от нуля Для неэффективного ограничения равна
- 8. Анализ оптимального плана 2. Двойственные оценки Двойственная оценка (д.о.) ограничения i показывает, на сколько изменится целевая
- 9. Анализ оптимального плана 2. Двойственные оценки Примеры: при увеличении объёма переработки молока в смену со 140
- 10. Анализ оптимального плана 2. Двойственные оценки Примеры: включение в модель новой переменной «сметана диетическая» в предположении,
- 11. Анализ оптимального плана 2. Двойственные оценки и адекватность модели Величина объективно обусловленной оценки (о.о.о.) каждого ресурса
- 12. Анализ оптимального плана 3. Анализ устойчивости оптимального плана Цель анализа – определить возможные изменения модели, при
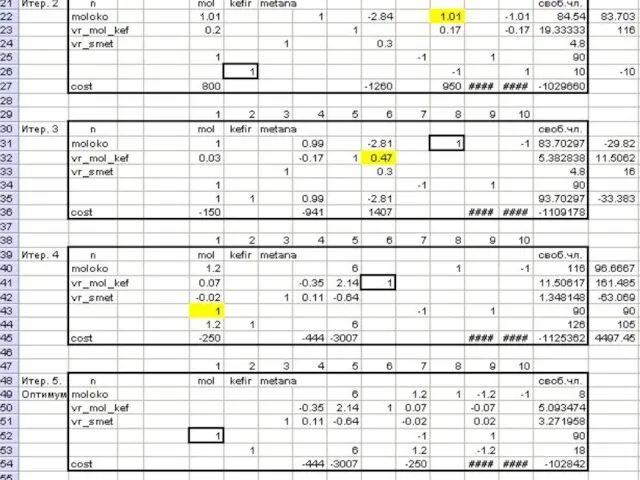
- 13. Анализ оптимального плана 3. Cимплексные таблицы ♦ Решаем…
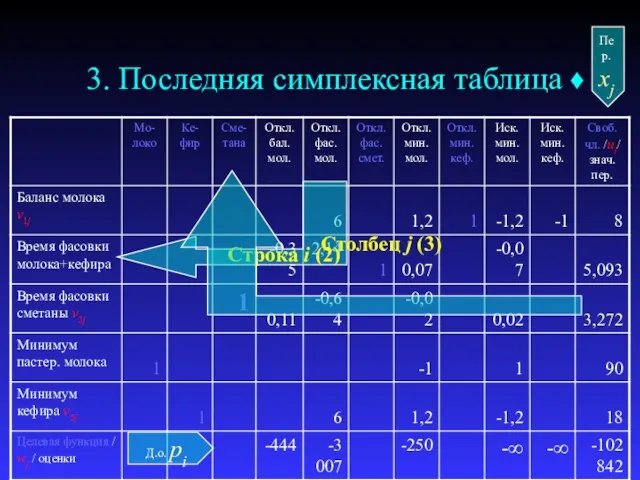
- 14. 3. Последняя симплексная таблица ♦
- 15. Анализ оптимального плана 3. Оптимальный план остаётся неизменным, если: коэффициент целевой функции при небазисной переменной меняется
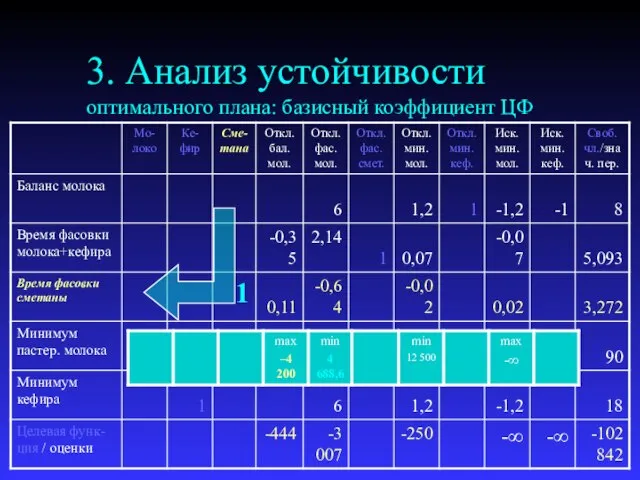
- 16. 3. Анализ устойчивости оптимального плана: базисный коэффициент ЦФ
- 17. Анализ оптимального плана 3. Оценки оптимального плана остаются неизменными, если: свободный член эффективного ограничения типа «меньше
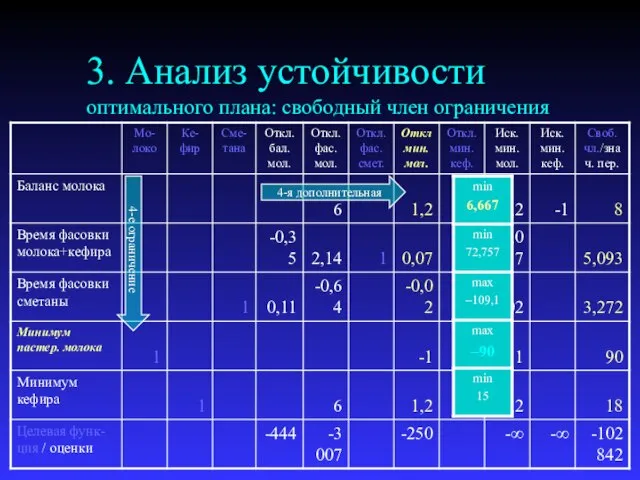
- 18. 3. Анализ устойчивости оптимального плана: свободный член ограничения 4-я дополнительная 4-е ограничение
- 19. Анализ оптимального плана 3. Анализ устойчивости оптимального плана может также проводиться по отношению к: Пределу введения
- 20. Анализ оптимального плана Все ли коэффициен-ты при этой переменной на месте?! Достаточно ли имеющихся ограничений? 4.
- 21. Анализ оптимального плана 4. Техника отладки моделей: причины несовместности системы ограничений Отрицательный результат эксперимента на модели
- 22. Анализ оптимального плана 4. Техника отладки моделей: ♦ поиск причин несовместности системы ограничений Если эффективных ограничений
- 23. Анализ оптимального плана 4. Техника отладки моделей Несовместность никогда не может быть вызвана: ошибкой в целевой
- 24. Анализ оптимального плана 4. Техника отладки моделей: неадекватное оптимальное решение Причины те же, что и при
- 26. Скачать презентацию



















 Изображение пейзажа, поэтапно
Изображение пейзажа, поэтапно The Coffee Love
The Coffee Love Благотворительный международныйтурнир журналистов по баскетболу «КУБОК НАДЕЖДЫ» г. Санкт-Петербург
Благотворительный международныйтурнир журналистов по баскетболу «КУБОК НАДЕЖДЫ» г. Санкт-Петербург «Река Руза. Берега бессмертия».
«Река Руза. Берега бессмертия». «Сегодня Нет Шансов Выжить на войне Без Хорошего Оружия и Инструментов. Многие люди оказались там с голыми руками. А Нам Повезло
«Сегодня Нет Шансов Выжить на войне Без Хорошего Оружия и Инструментов. Многие люди оказались там с голыми руками. А Нам Повезло  Neuropsychology of Memory
Neuropsychology of Memory  Cтраны Северной Африки
Cтраны Северной Африки О комплексе мер по профилактике травматизма обучающихся и воспитанников. Порядок расследования несчастных случаев с обучающимис
О комплексе мер по профилактике травматизма обучающихся и воспитанников. Порядок расследования несчастных случаев с обучающимис Возможности контроля выбросов в странах-нечленах ЕС
Возможности контроля выбросов в странах-нечленах ЕС Бухгалтерский учет
Бухгалтерский учет Анализ текущей ситуации в российской банковской системе
Анализ текущей ситуации в российской банковской системе Презентация на тему Компьютер и ПО
Презентация на тему Компьютер и ПО Технология создания gif-анимации в Photoshop или ImageReady
Технология создания gif-анимации в Photoshop или ImageReady ББЗ - школьникам
ББЗ - школьникам Памятники Калининграда как текст
Памятники Калининграда как текст Калининградская область, Зеленоградский район Население – 32,5 тыс. чел. Территория – 2 016 кв. км Глава муниципального образования –
Калининградская область, Зеленоградский район Население – 32,5 тыс. чел. Территория – 2 016 кв. км Глава муниципального образования –  Richard I
Richard I Коренной перелом в ходе войны
Коренной перелом в ходе войны Движения играют роль в нашей жизни?
Движения играют роль в нашей жизни? Что такое техника
Что такое техника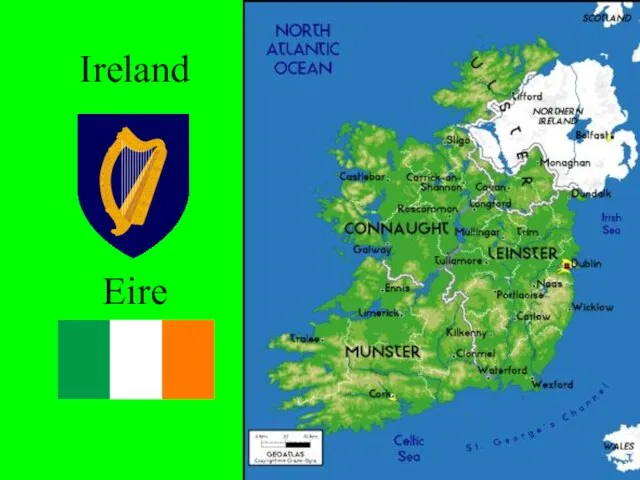 Ireland Eire The Cliffs of Moher
Ireland Eire The Cliffs of Moher Докладывает: Алексей Владимирович Бушуев, Пермский филиал ООО «Компания БКС»
Докладывает: Алексей Владимирович Бушуев, Пермский филиал ООО «Компания БКС» Конституционное право
Конституционное право Болонский процесс и связанные с ним изменения в секторе высшего образования- К взаимному признанию и пониманию необходимости кул
Болонский процесс и связанные с ним изменения в секторе высшего образования- К взаимному признанию и пониманию необходимости кул Город сегодня и завтра. Тенденции и перспективы развития современной архитектуры
Город сегодня и завтра. Тенденции и перспективы развития современной архитектуры Урок 01 Фізика як навчальний предмет
Урок 01 Фізика як навчальний предмет Сайдинг. Виды сайдинга
Сайдинг. Виды сайдинга Большие и мелкие кошки
Большие и мелкие кошки