Содержание
- 2. Линейная модель использования кормов 1. Цель моделирования Заготовленные в хозяйстве корма могут быть использованы различными способами.
- 3. Линейная модель использования кормов 1. Постановка задачи Определить план использования заготовленных кормов в течение заданного периода,
- 4. Линейная модель использования кормов 2. Математическое представление модели (вариант с заданными рационами) Переменные Количество корма каждого
- 5. 2. Математическое представление модели (вариант с заданными рационами) ♦ Ограничения По наличию кормов (ц): ixj1 ≤
- 6. Линейная модель использования кормов Математическое представление модели (вариант с заданными рационами) Целевая функция: максимум продуктивности (тыс.
- 7. Линейная модель использования кормов 2. Математическое представление модели (вариант с заданными рационами) Как упростить модель Ограничение
- 8. Линейная модель использования кормов 2. Математическое представление модели (вариант с оптимизацией рационов) Переменные Количество корма каждого
- 9. 2. Математическое представление модели (вариант с оптимизацией рационов) Ограничения По наличию кормов (без изменений); По балансу
- 10. 2. Математическое представление модели (вариант с оптимизацией рационов) По допустимой доле кормов различных групп в общей
- 11. Линейная модель использования кормов 2. Математическое представление модели (вариант с оптимизацией рационов) Целевая функция: максимум продуктивности
- 12. Линейная модель использования кормов 3. Разработка числовой модели Множество видов кормов определяется: наличием запасов корма данного
- 13. Линейная модель использования кормов 3. Разработка числовой модели (вариант с заданными рационами) ♦ bj1 — по
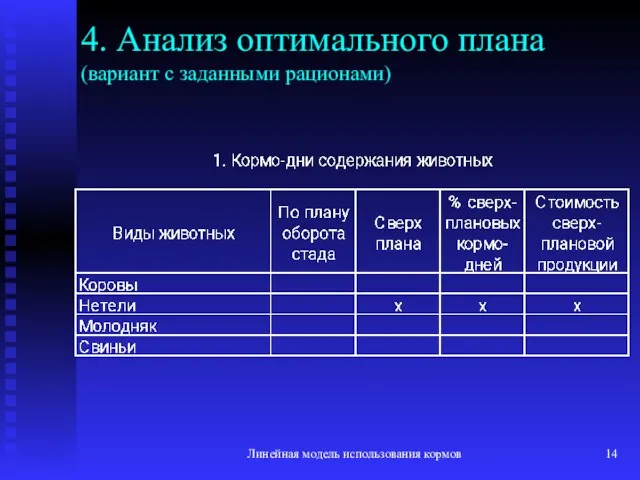
- 14. Линейная модель использования кормов 4. Анализ оптимального плана (вариант с заданными рационами)
- 15. Линейная модель использования кормов 4. Анализ оптимального плана
- 16. 4. Анализ оптимального плана
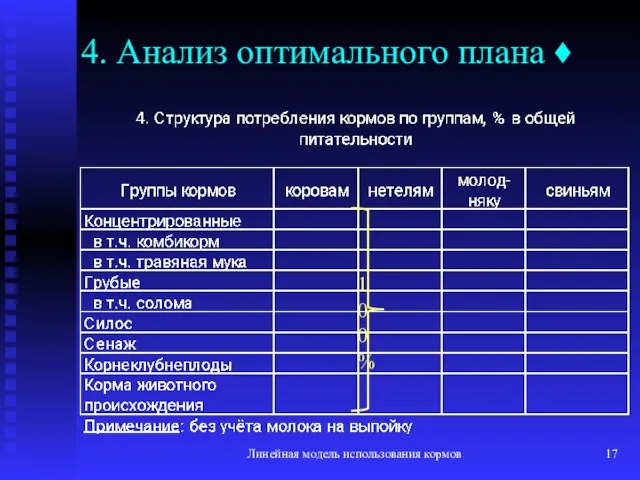
- 17. Линейная модель использования кормов 4. Анализ оптимального плана ♦ 100%
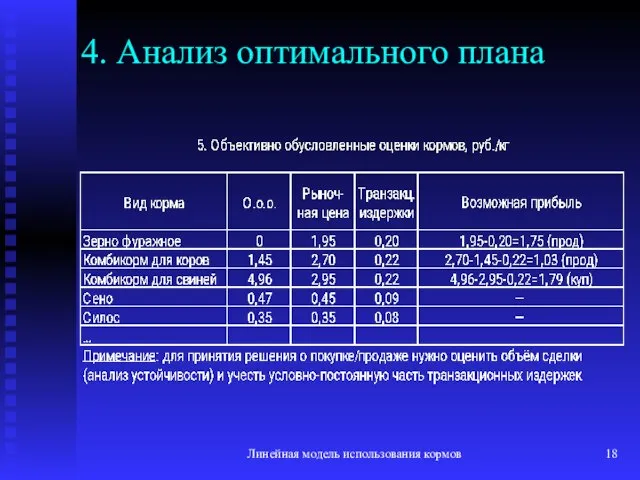
- 18. Линейная модель использования кормов 4. Анализ оптимального плана
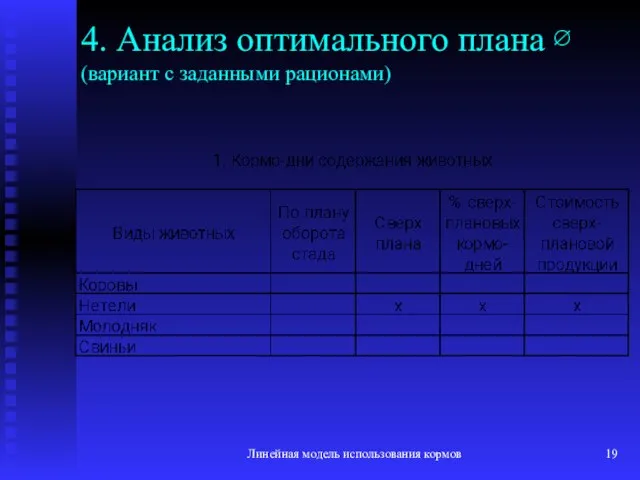
- 19. Линейная модель использования кормов 4. Анализ оптимального плана ∅ (вариант с заданными рационами)
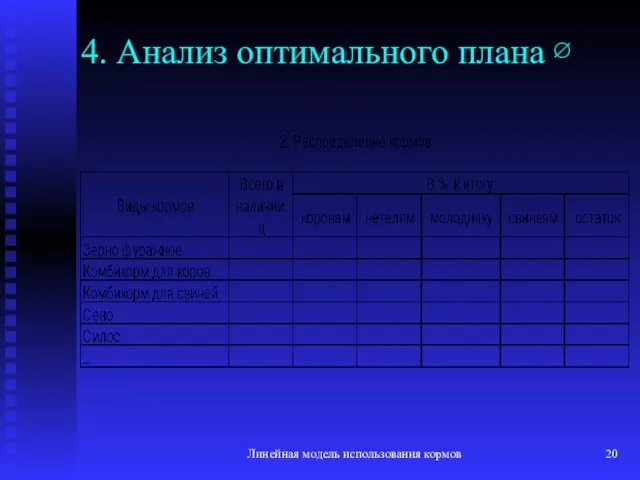
- 20. Линейная модель использования кормов 4. Анализ оптимального плана ∅
- 21. 4. Анализ оптимального плана ∅
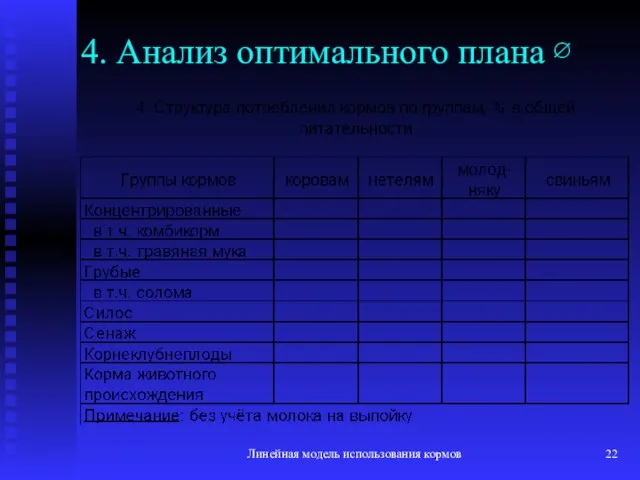
- 22. Линейная модель использования кормов 4. Анализ оптимального плана ∅
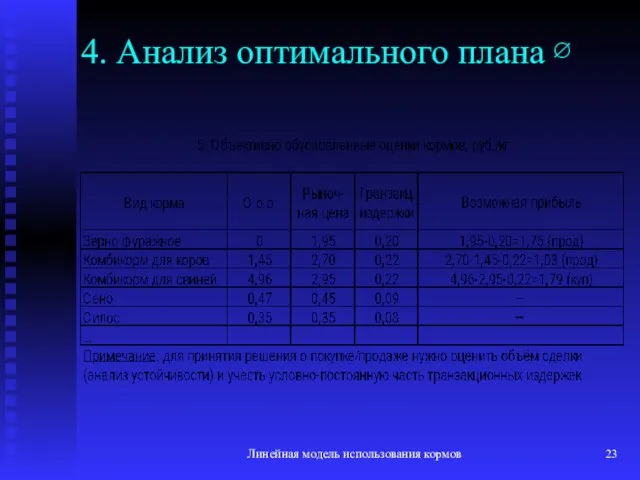
- 23. Линейная модель использования кормов 4. Анализ оптимального плана ∅
- 24. Линейная модель использования кормов 4. Анализ оптимального плана: двойственные оценки (вариант с заданными рационами) Оценки по
- 25. 5. Развитие моделей использования кормов Недостатки модели: не учитываются дополнительные затраты, связанные с увеличением количества кормо-дней;
- 27. Скачать презентацию

















 Лучшая кормушка для птиц
Лучшая кормушка для птиц Conflicts
Conflicts Искусство бумагокручения. Знакомство с квиллингом
Искусство бумагокручения. Знакомство с квиллингом Презентация на тему Уход за больным. Выдача листа нетрудоспособности
Презентация на тему Уход за больным. Выдача листа нетрудоспособности  Презентация на тему Подвиги детей во время Великой Отечественной войны
Презентация на тему Подвиги детей во время Великой Отечественной войны  Школа – центральное звено в системе общей профилактики отклоняющего поведения
Школа – центральное звено в системе общей профилактики отклоняющего поведения Варлам Шаламов 1907 -1982
Варлам Шаламов 1907 -1982 Развитие сети профессиональных юридических услуг в России и СНГ Альберт Еганян, к.ю.н., MCIArb, Управляющий партнер
Развитие сети профессиональных юридических услуг в России и СНГ Альберт Еганян, к.ю.н., MCIArb, Управляющий партнер КВН
КВН Экологические проблемы Байкала
Экологические проблемы Байкала Методические рекомендации к преподаванию модуля Основы православной культуры в курсе «Основы религиозных культур и светской эти
Методические рекомендации к преподаванию модуля Основы православной культуры в курсе «Основы религиозных культур и светской эти Портфоліо викладача
Портфоліо викладача Спорт
Спорт Моделирование текста
Моделирование текста Категории электроприемников
Категории электроприемников Presentatie Welcome
Presentatie Welcome Новости на МашДаш ТВ
Новости на МашДаш ТВ Вредоносные программыМетоды профилактики и защиты
Вредоносные программыМетоды профилактики и защиты Описание системы
Описание системы История архитектуры и градостроительства. Архитектура Высокого Возрождения
История архитектуры и градостроительства. Архитектура Высокого Возрождения Презентация на тему Понятие о местоимении. Местоимения 1, 2, 3-го лица
Презентация на тему Понятие о местоимении. Местоимения 1, 2, 3-го лица Правовые механизмы стимулирования промышленных предприятий Как эффективно использовать возможности действующего законодатель
Правовые механизмы стимулирования промышленных предприятий Как эффективно использовать возможности действующего законодатель Кондитерская Zoetrope. Торт – оптическая иллюзия
Кондитерская Zoetrope. Торт – оптическая иллюзия Техника нападающего удара
Техника нападающего удара Право и закон
Право и закон Сравнение гусеничного и колесного роботов с одинаковыми техническими характеристиками при движении по пересеченной местности
Сравнение гусеничного и колесного роботов с одинаковыми техническими характеристиками при движении по пересеченной местности Версальско – Вашингтонская система
Версальско – Вашингтонская система Речевая азбука
Речевая азбука