Тема урока: «Параллелограмм, прямоугольник, ромб, квадрат и их свойства, формулы для вычисления их площадей».

Цель: систематизация знаний по теме “Четырехугольники”.

Много ль времени, аль мало
С той поры уж пробежало
За горами, за лесами,
За широкими морями,
Против неба – на земле
Жил старик в одном селе.
Четырехугольником он звался,
Род великий начинался
С старика того. Так вот.
У старинушки два сына
Все в отца, да вот причина:
Был один из них горбат,
А другой “пузоковат”.
Кто такие эти дети
Может знает кто на свете?

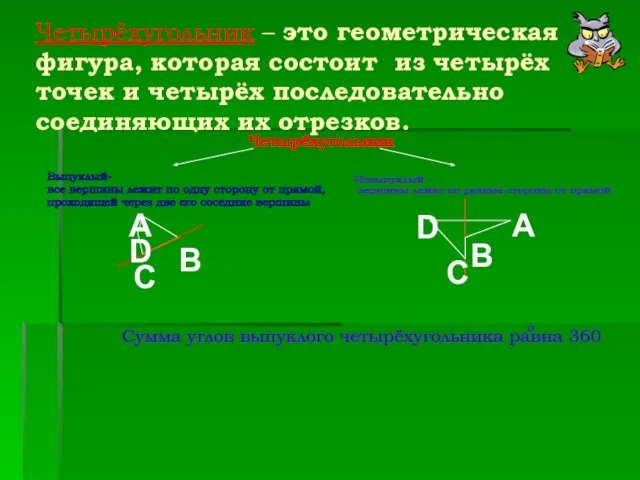
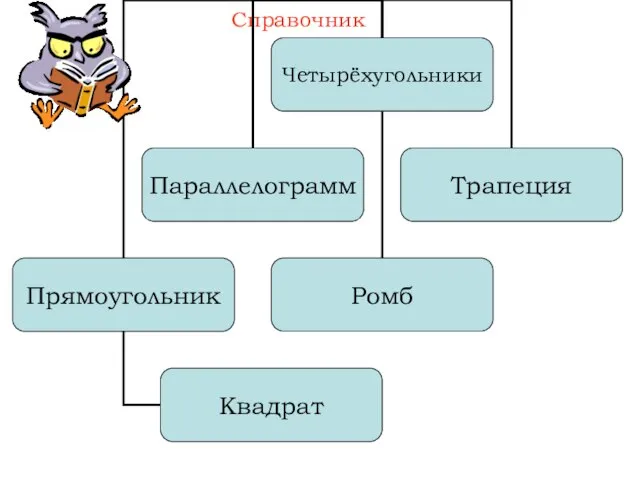
Четырёхугольник – это геометрическая фигура, которая состоит из четырёх точек и четырёх последовательно соединяющих их отрезков.

Время катит чередом,
Час за часом, день за днём,-
Прибавляя с каждым годом,
Разрослась семья народом.

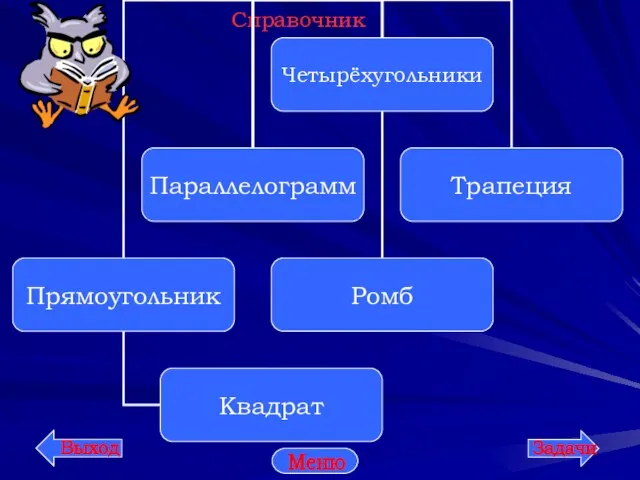
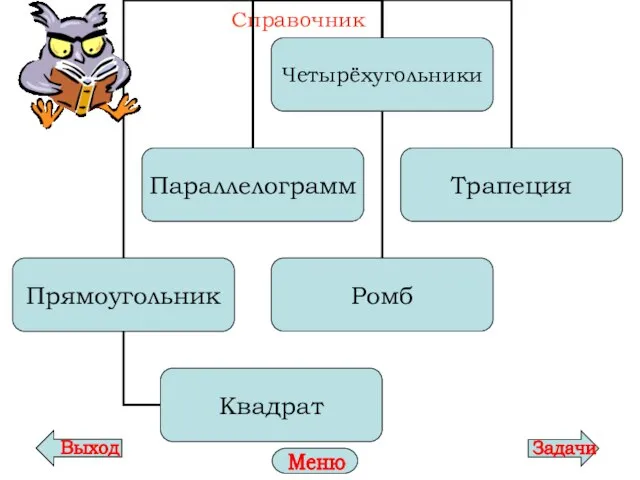
Справочник
Меню

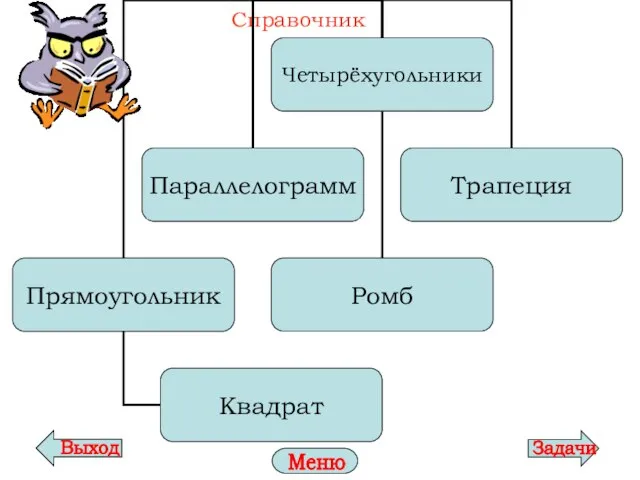
Параллелограмм – четырёхугольник, у которого противоположные стороны попарно параллельны
Свойства параллелограмма
Признаки параллелограмма
Площадь параллелограмма
Частные виды параллелограмма: прямоугольникЧастные виды параллелограмма: прямоугольник и ромб
AB || CD
BC || AD

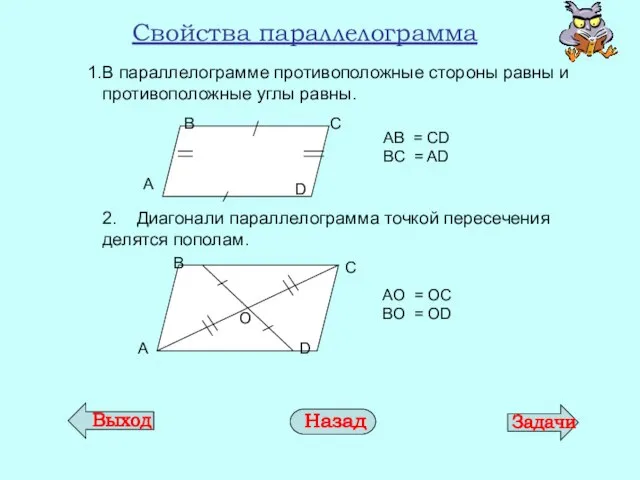
Свойства параллелограмма
В параллелограмме противоположные стороны равны и противоположные углы равны.
2. Диагонали параллелограмма точкой пересечения делятся пополам.
AB = CD
BC = AD
AО = ОC
BО = ОD

Признаки параллелограмма
Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник – параллелограмм.
Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник – параллелограмм.
3. Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм.
BC || AD
BC = AD
AО = ОC
BО = ОD
BC = AD
АB = СD

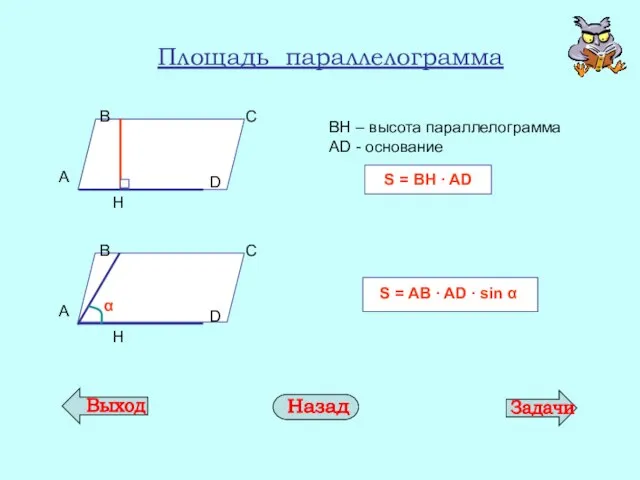
Площадь параллелограмма
ВН – высота параллелограмма
AD - основание
S = BH ∙ AD
A
D
B
C
Н
α
S = AB ∙ AD ∙ sin α

Справочник
Меню

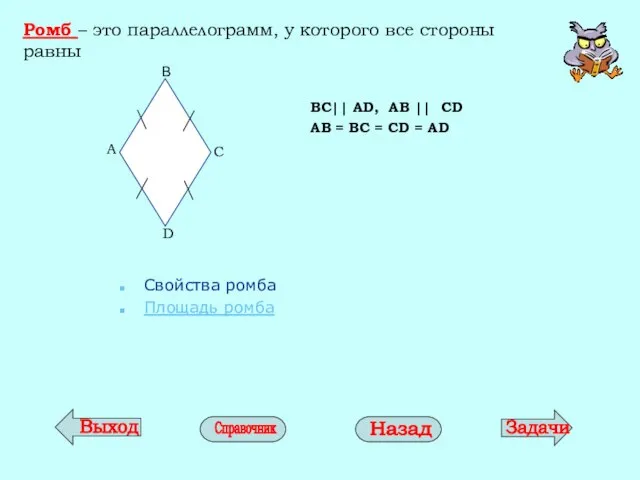
Ромб – это параллелограмм, у которого все стороны равны
BC|| AD, AB || CD
AB = BC = CD = AD
Свойства ромба
Площадь ромба

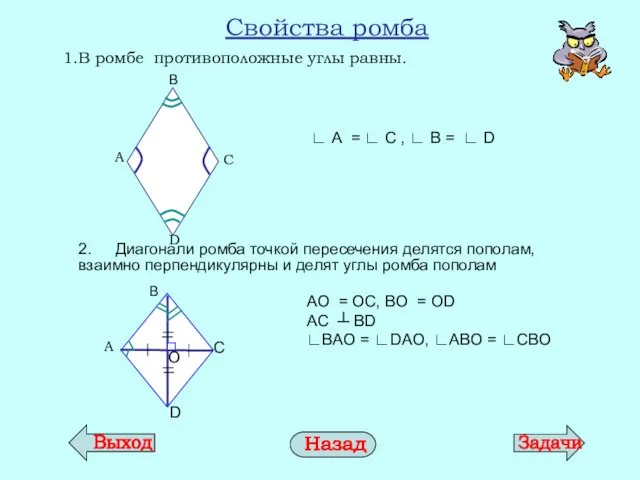
Свойства ромба
В ромбе противоположные углы равны.
2. Диагонали ромба точкой пересечения делятся пополам, взаимно перпендикулярны и делят углы ромба пополам
∟ А = ∟ С , ∟ В = ∟ D
AО = ОC, BО = ОD
AC ┴ BD
∟BAO = ∟DAO, ∟ABO = ∟CBO

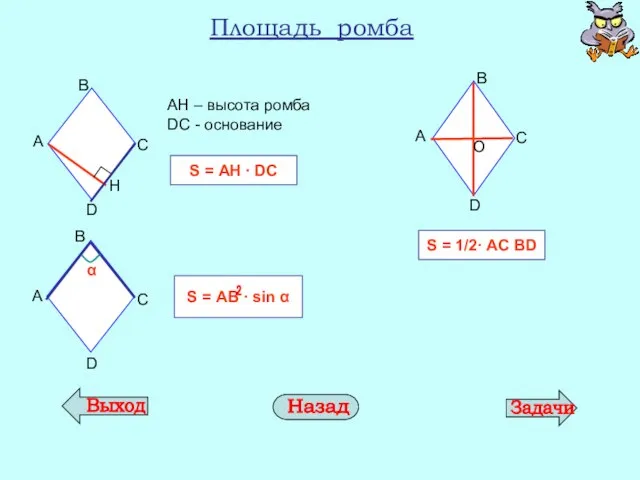
Площадь ромба
АН – высота ромба
DС - основание
S = АH ∙ DС
А
D
O
B
C
S = 1/2∙ АC BD

Справочник
Меню

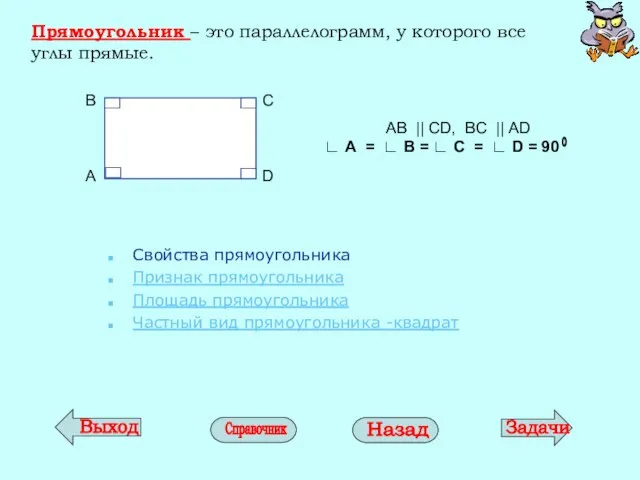
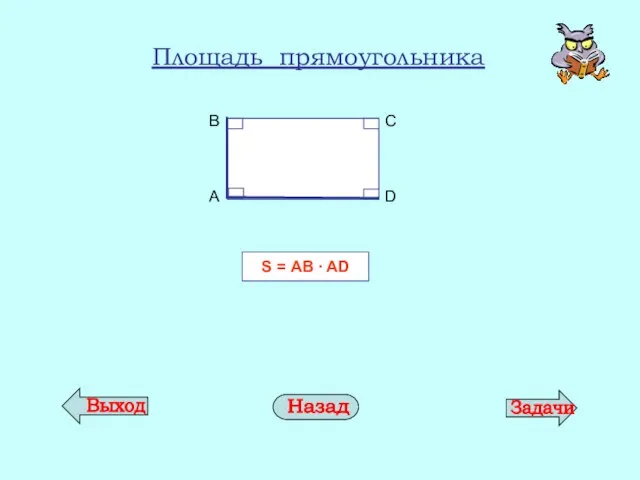
Прямоугольник – это параллелограмм, у которого все углы прямые.
Свойства прямоугольника
Признак прямоугольника
Площадь прямоугольника
Частный вид прямоугольника -квадрат
AB || CD, BC || AD
∟ А = ∟ В = ∟ С = ∟ D = 90
о

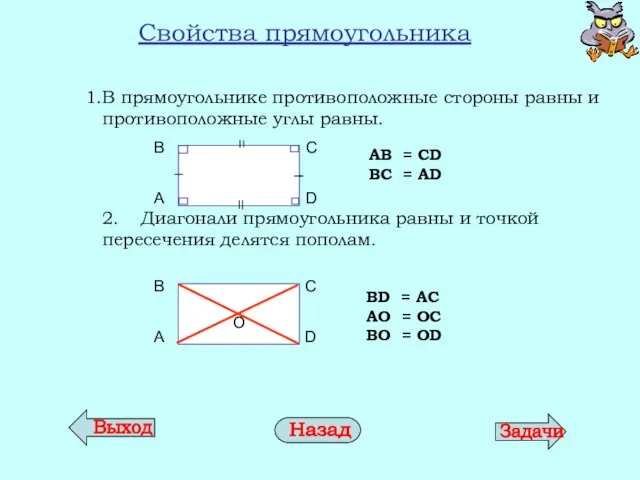
Свойства прямоугольника
В прямоугольнике противоположные стороны равны и противоположные углы равны.
2. Диагонали прямоугольника равны и точкой пересечения делятся пополам.
AB = CD
BC = AD
BD = AC
AО = ОC
BО = ОD

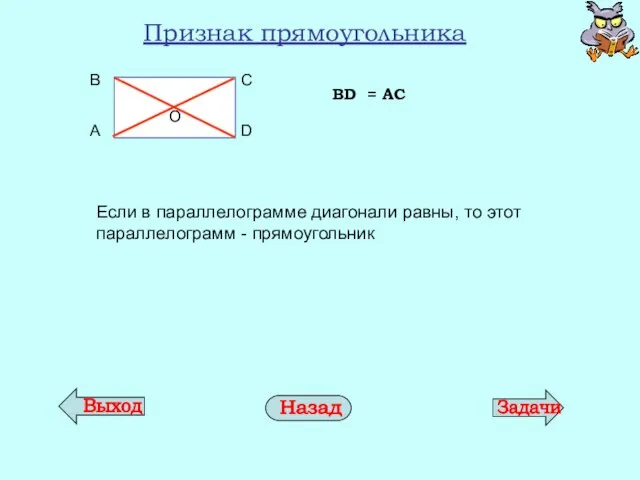
Признак прямоугольника
Если в параллелограмме диагонали равны, то этот параллелограмм - прямоугольник
BD = AC

Площадь прямоугольника
S = АB ∙ AD

Справочник

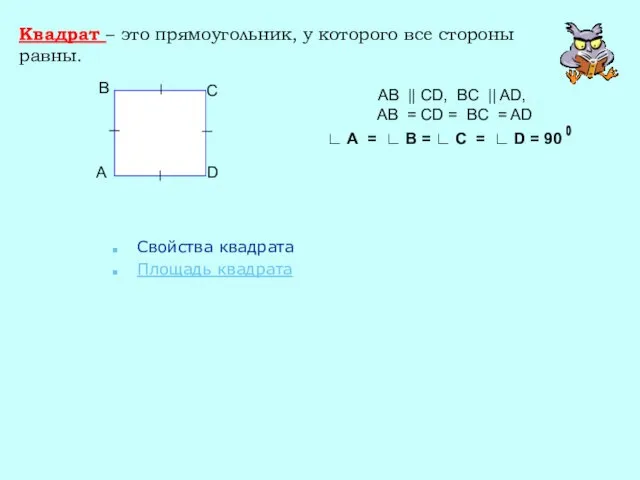
Квадрат – это прямоугольник, у которого все стороны равны.
Свойства квадрата
Площадь квадрата AB || CD, BC || AD, ,
AB = CD = BC = AD
о
∟ А = ∟ В = ∟ С = ∟ D = 90

Свойства квадрата
У квадрата все стороны равны и все углы равны.
2. Диагонали квадрата взаимно перпендикулярны, равны, точкой пересечения делятся пополам и делят углы квадрата пополам.
AB = CD = BC = AD
∟ А = ∟ В = ∟ С = ∟ D = 90
AC ┴ BD
BD = AC
AО = ОC, BО = ОD
∟BAO = ∟DAO, ∟ABO = ∟CBO
о

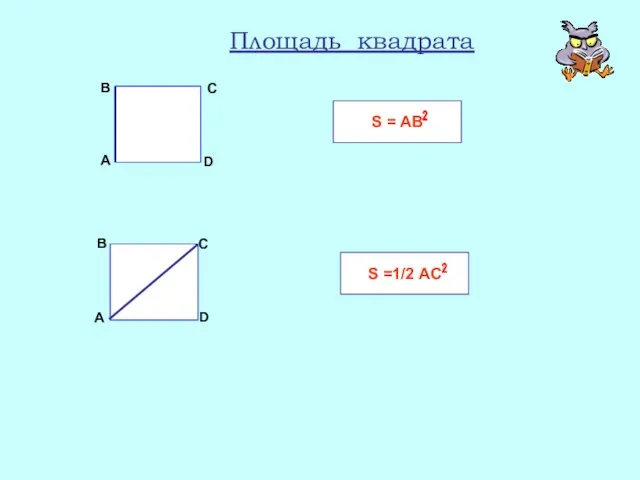
Площадь квадрата
А
В
С
D
А
В
С
D

Справочник

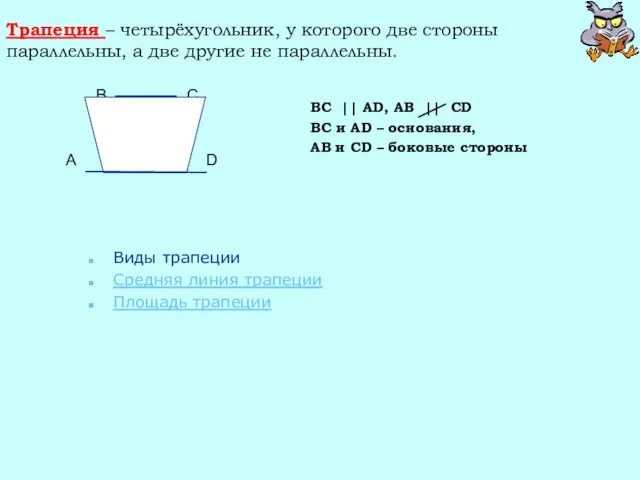
Трапеция – четырёхугольник, у которого две стороны параллельны, а две другие не параллельны.
BC || AD, AB || CD
BC и AD – основания,
AB и CD – боковые стороны
Виды трапеции
Средняя линия трапеции
Площадь трапеции

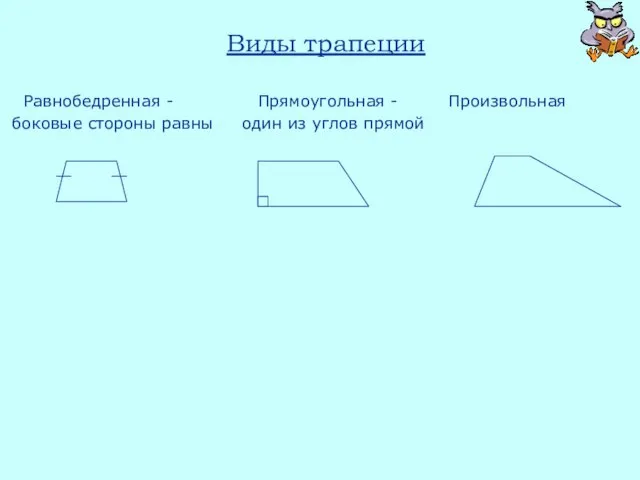
Виды трапеции
Равнобедренная - Прямоугольная - Произвольная
боковые стороны равны один из углов прямой

Средняя линия трапеции
Средняя линия трапеции – это отрезок, соединяющий середины боковых сторон.
MN- средняя линия
М
N
Средняя линия трапеции параллельна основаниям и равна их полусумме
MN || AD, MN || AD,
MN = (BC + AD) / 2

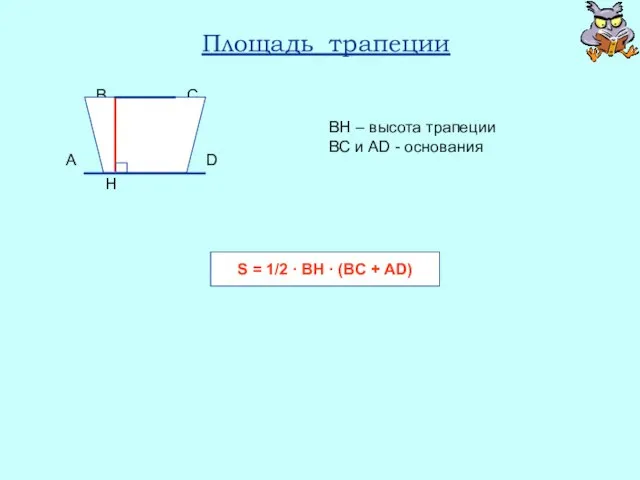
Площадь трапеции
ВН – высота трапеции
ВС и AD - основания
S = 1/2 ∙ BH ∙ (ВС + AD)
H

Задачник
задачник

Четырёхугольник
Найдите углы выпуклого четырёхугольника, если они равны друг другу.
Найдите углы выпуклого четырёхугольника, если они пропорциональны числам 1,2,4,5.
Найдите стороны четырёхугольника, если его периметр равен 8 см, а одна сторона больше каждой из других сторон соответственно на 3 мм, 4мм и 5мм.
Найдите стороны четырёхугольника, если его периметр равен 66 см, первая сторона больше второй на 8 см и на столько же меньше третьей стороны, а четвёртая в три раза больше второй.
Докажите, что если не все углы выпуклого четырёхугольника равны друг другу, то хотя бы один из них тупой.

Параллелограмм
Периметр параллелограмма равен 48 см. Найдите стороны параллелограмма, если разность двух сторон равна 7 см.
Найдите углы параллелограмма, если сумма противолежащих углов равна 142.
Найдите периметр параллелограмма, если биссектриса одного из его углов делит сторону параллелограмма на отрезки 7 см и 14 см.
На диагонали BD параллелограмма ABCD отмечены точки P и Q так, что PB = QD. Докажите, что четырёхугольник APCQ – параллелограмм.
В параллелограмме, смежные стороны которого не равны, проведены биссектрисы углов. Докажите, что при их пересечении образуется прямоугольник.

Ромб
Найдите периметр ромба ABCD, в котором ∟ В = 60, АС= 10,5 см.
Найдите углы ромба, если основание перпендикуляра, опущенного из вершины тупого угла, делит сторону ромба пополам.
Найдите диагонали ромба, если одна из них в 1,5 раза больше другой, а площадь ромба равна 27 кв. см.
Сторона ромба равна 24 см, а один из его углов 150 . Найдите расстояние между его противолежащими сторонами
Из вершины В ромба ABCD, проведены перпендикуляры ВК и ВМ к прямым AD и DC. Докажите, что луч BD является биссектрисой ∟КВМ.
о
о

Прямоугольник
Диагонали прямоугольника ABCD пересекаются в точке О. Докажите, что
треугольники АОВ и АОD равнобедренные.
Биссектриса одного из углов прямоугольника делит большую сторону пополам. Найдите периметр прямоугольника, если его меньшая сторона 12 см.
Стороны прямоугольника относятся как 2 : 7. Найдите стороны прямоугольника, если его площадь равна 108 кв.см.
Сторона прямоугольника равна 4 см и образует с диагональю угол 60. Найдите эту диагональ.
Пол комнаты, имеющий форму прямоугольника со сторонами 5,5 м и 6 м, нужно покрыть паркетом прямоугольной формы. Длина каждой дощечки паркета равна 30 см, а ширина – 5 см. Сколько потребуется таких дощечек для покрытия пола?
о

Квадрат
Является ли четырёхугольник квадратом, если его диагонали:
а) равны и взаимно перпендикулярны;
б) взаимно перпендикулярны и имеют общую середину;
в) равны, взаимно перпендикулярны и имеют общую середину.
2. Диагональ квадрата 24 см. Найдите периметр четырёхугольника,
образованного отрезками, последовательно соединяющими
середины сторон данного квадрата.
Сторону квадрата увеличили в 3 раза. Во сколько раз увеличилась его площадь?
Площадь квадрата равна 18 кв.см. Найдите диагональ квадрата.
В равнобедренный прямоугольный треугольник вписан квадрат так,
что две его вершины находятся на гипотенузе, а другие две – на катетах.
Найдите сторону квадрата, если известно, что гипотенуза равна 12 см.

Трапеция
Найдите углы B и D трапеции ABCD с основаниями AD и BC, если ∟А = 36 ,∟С= 117 .
Докажите, что трапеция равнобедренная, если её диагонали равны.
Основания прямоугольной трапеции равны 10 см, 15 см, а один из углов – 45 .Найдите меньшую боковую сторону трапеции.
Найдите площадь равнобедренной трапеции. Если её основания равны 16 см и 30 см, а диагонали взаимно перпендикулярны.
Боковые стороны трапеции равны 13 см и 15 см, а периметр равен 48 см. Найдите среднюю линию трапеции
о
о
о

Проверь себя

Задание № 1
Какое из утверждений неверное:
квадрат является одновременно параллелограммом и прямоугольником;
угол между стороной и диагональю квадрата равен 45 ;
существует квадрат, который не является ромбом;
диагонали квадрата взаимно перпендикулярны.

Задание № 2
Найдите площадь ромба, диагонали которого равны 26 см и 8 см:
208 кв.см ;
104 кв.см;
52 кв.см;
68 кв.см

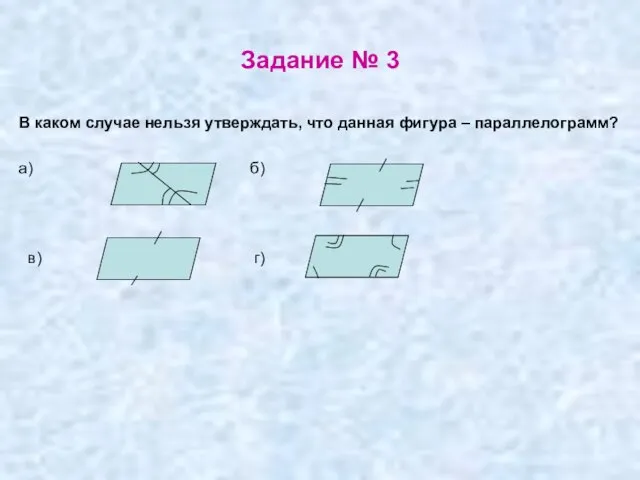
Задание № 3
В каком случае нельзя утверждать, что данная фигура – параллелограмм?
а) б)
в) г)

Задание № 4
Диагонали прямоугольника ABCD пересекаются в точке О. Определите периметр треугольника АВО, если АВ = 6 см, а диагональ прямоугольника равна 14 см:
19 см ;
26 см;
20 см;
18 см

Задание № 5
Какое из утверждений неверное?
у прямоугольника углы прямые, а у ромба не обязательно;
у ромба диагонали взаимно перпендикулярны, а у прямоугольника не обязательно;
у ромба диагонали являются биссектрисами его углов, а у параллелограмма не обязательно;
у ромба диагонали равны, а у прямоугольника не обязательно;

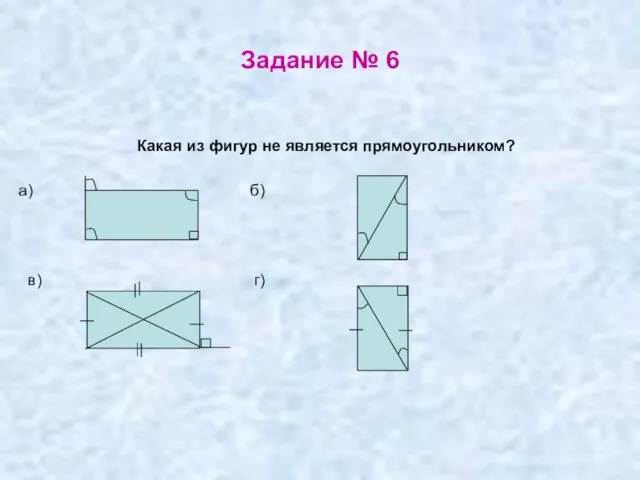
Задание № 6
Какая из фигур не является прямоугольником?
а) б)
в) г)

Задание № 7
В прямоугольнике ABCD проведена биссектриса АМ. ВМ= 5см,
МС =4 см. Найдите площадь прямоугольника:
36 кв. см
45 кв. см
28 кв. см
56 кв.см

Задание № 8
Найти площадь трапеции ABCD с основаниями AB и CD, если BC перпендикулярна AB, AB= 5 см, BC= 8 см, CD= 13 см.
144 кв.см;
36 кв.см;
72 кв.см;
70 кв.см

Задание № 9
Какое из утверждений неверное?
параллелограмм, у которого диагонали взаимно перпендикулярны, является квадратом;
прямоугольник, у которого все стороны равны, является квадратом;
ромб у которого один угол прямой, является квадратом;
ромб, у которого диагонали равны, является квадратом

Задание № 10
Найдите высоту параллелограмма, если его площадь
равна 75,6 кв. см, а основание - 14 см.
23,8 см ;
5,4 см;
61,6 см;
16 см.